九、递归
理解递归
在数学与计算机科学中,递归(Recursion)是指在函数的定义中使用函数自身的方法,直观上来看,就是某个函数自己调用自己。
递归需要满足的三个条件
- 一个问题的解可以分解为几个子问题的解,子问题就是数据规模更小的问题。
- 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样。
- 存在递归终止条件,把问题分解为子问题,把子问题再分解为子子问题,一层一层分解下去,不能存在无限循环,这就需要有终止条件。
编写递归代码的方法:
- 写递归代码最关键的是写出递推公式,找到终止条件。
- 将递推公式转化为代码。
举个例子:
- 假如有 n 个台阶,每次可以跨 1 个台阶或者 2 个台阶,请问走这 n 个台阶有多少种走法?
- 如果有7个台阶,可以2, 2, 2, 1这样子上去,也可以1, 2, 1, 1, 2这样子上去,总之走法有很多,那如何用编程求得总共有多少种走法?
- 可以根据第一步的走法把所有走法分为两类,第一类是第一步走了 1 个台阶,另一类是第一步走了 2 个台阶。
- 所以 n 个台阶的走法就等于先走1阶后, n-1 个台阶的走法 加上先走2阶后, n-2 个台阶的走法。用公式表示就是:
- f(n) = f(n-1)+f(n-2)
- 递归终止条件是 f(1)=1, f(2) = 2。可以拿 n=3, n=4 验证一下,这个终止条件是否足够并且正确。
- 把递归终止条件和刚刚得到的递推公式放到一起就是这样的:
public static int test1(int n) {
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
return test1(n - 1) + test1(n - 2);
}
递归的优缺点:
- 优点:
- 代码简洁高效。表达能力强。
- 缺点:
- 函数调用会使用栈来保存临时变量。每调用一个函数,都会将临时变量封装为栈帧压入内存栈,等函数执行完成返回时,才出栈。
- 系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大,调用层次很深,一直压入栈,就会有堆栈溢出的风险。
- 在时间效率上,递归代码里多了很多函数调用,当这些函数调用的数量较大时,就会积聚成一个可观的时间成本。
- 在空间复杂度上,因为递归调用一次就会在内存栈中保存一次现场数据,所以在分析递归代码空间复杂度时,需要额外考虑这部分的开销。
汉诺塔问题
汉诺塔问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上,并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
-
这是一个大规模的复杂问题,如果要采用递归方法去解决的话,就要先把问题化简。
-
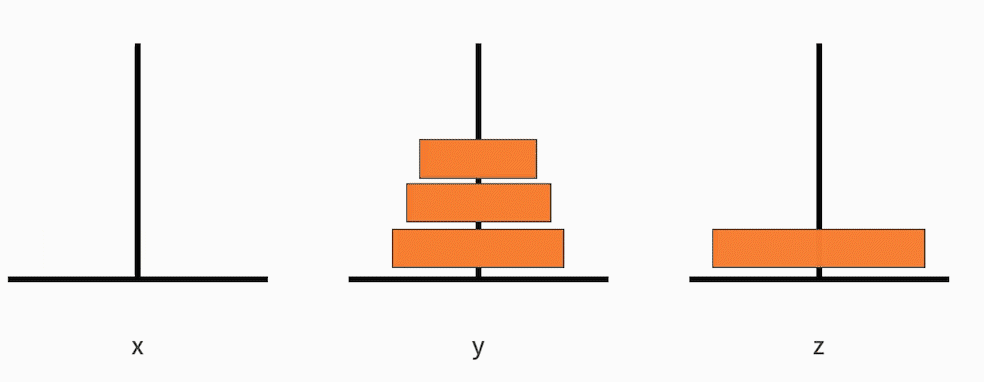
原问题是,把从小到大的 n 个盘子,从 x 移动到 z。
-
可以将这个大问题拆解为以下 3 个小问题:
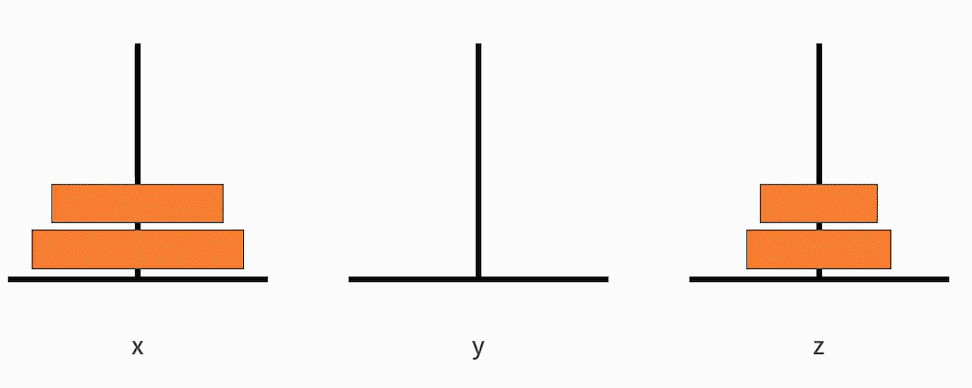
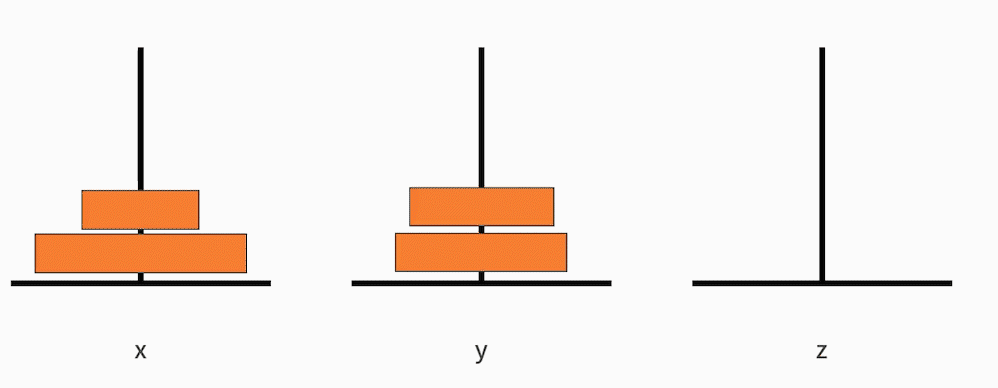
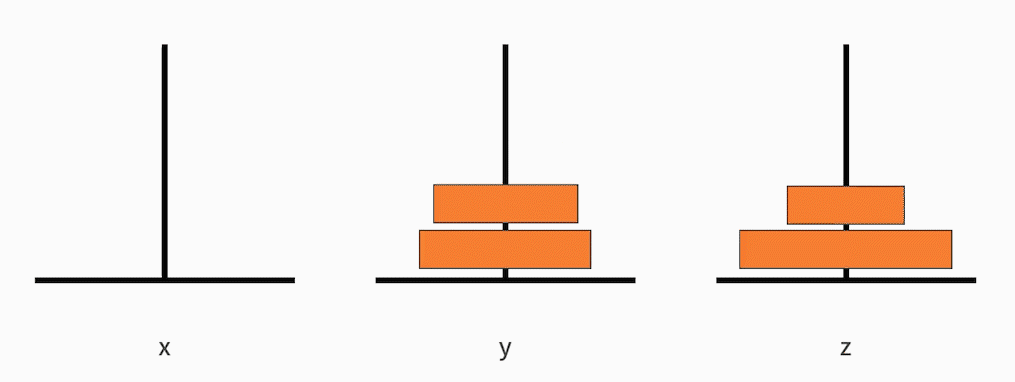
- 把从小到大的 n-1 个盘子,从 x 移动到 y;
- 接着把最大的一个盘子,从 x 移动到 z;
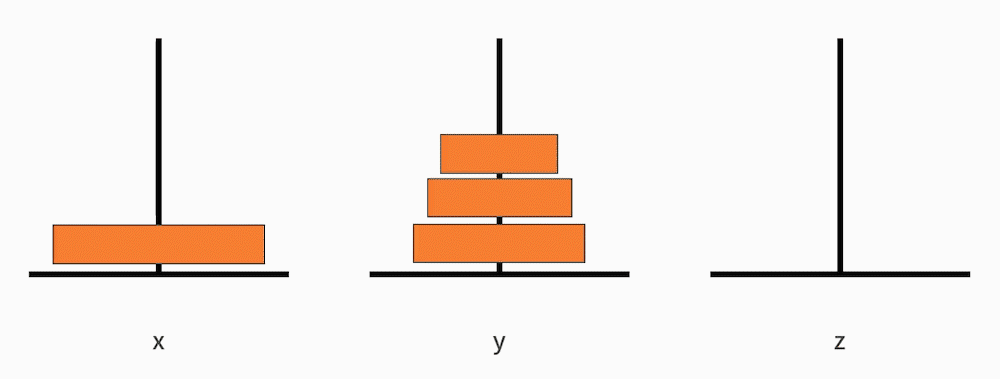
- 再把从小到大的 n-1 个盘子,从 y 移动到 z。
-
首先,来判断它是否满足递归的第一个条件。 其中,第 1 和第 3 个问题就是汉诺塔问题。
-
这样就完成了一次把大问题缩小为完全一样的小规模问题。
-
已经定义好了递归体,也就是满足来递归的第一个条件。如下图所示:
-
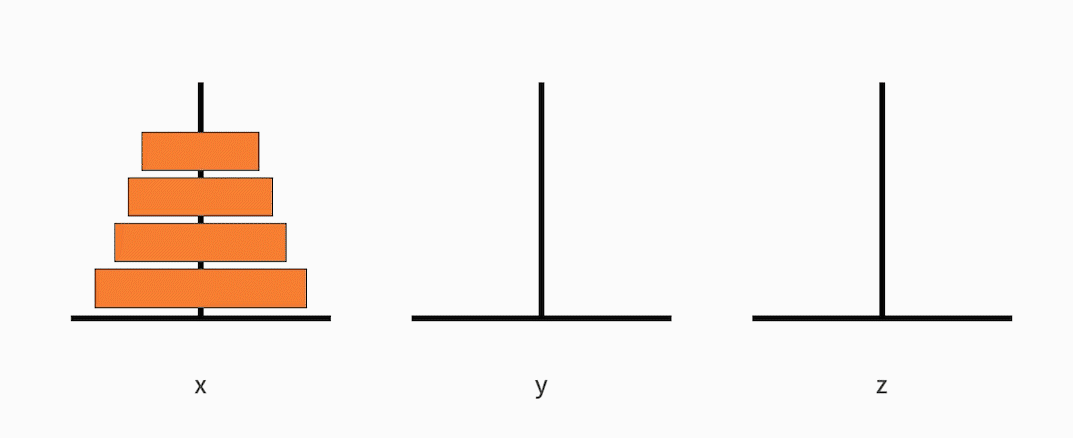
-
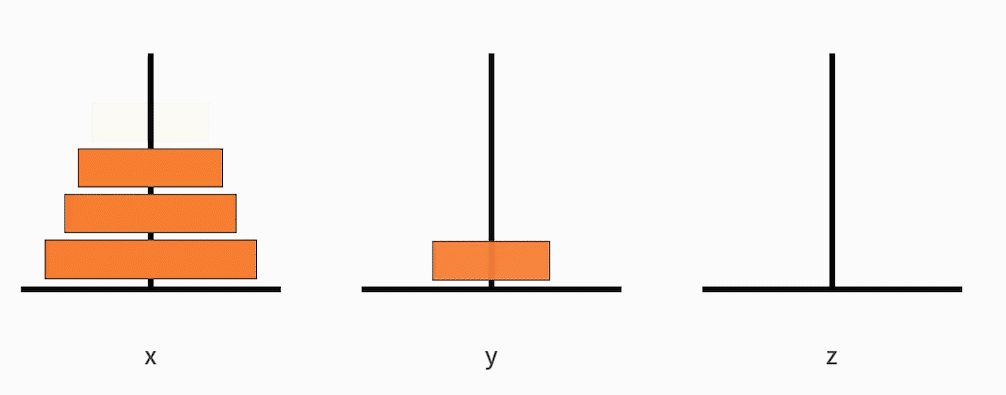
-
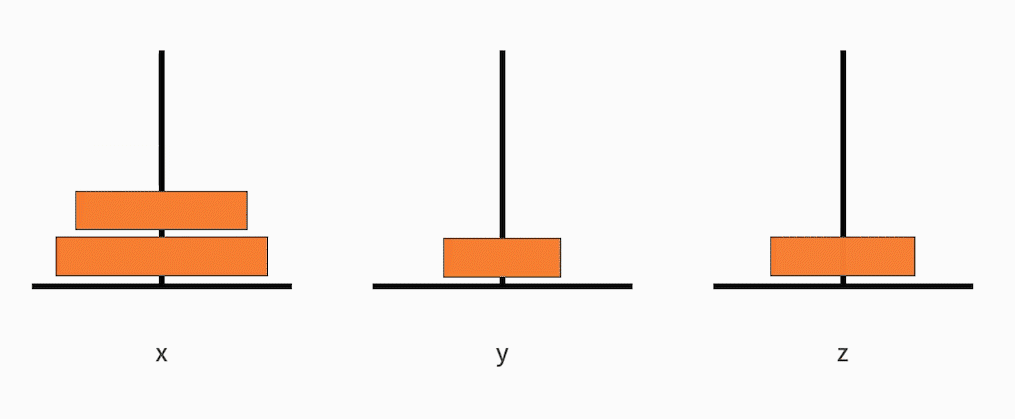
-
-
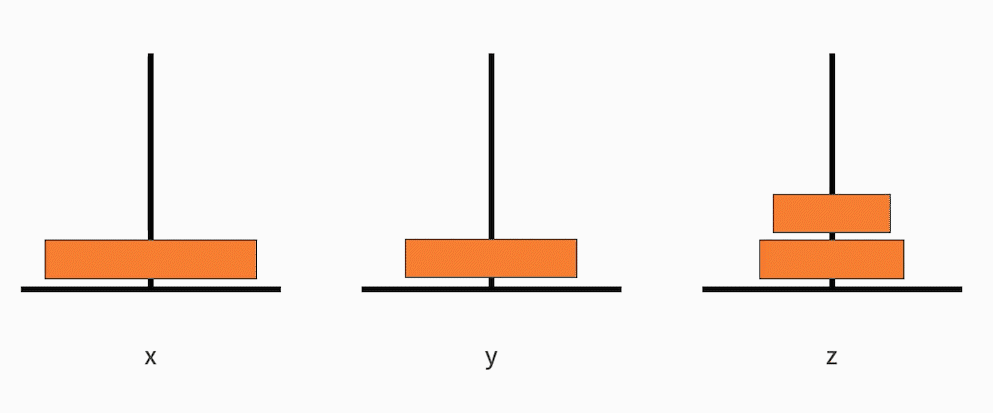
-
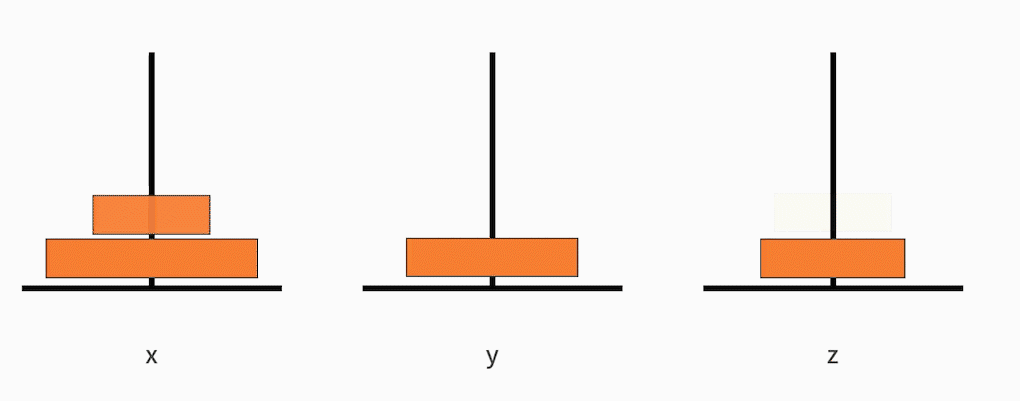
-
-
-
-
-
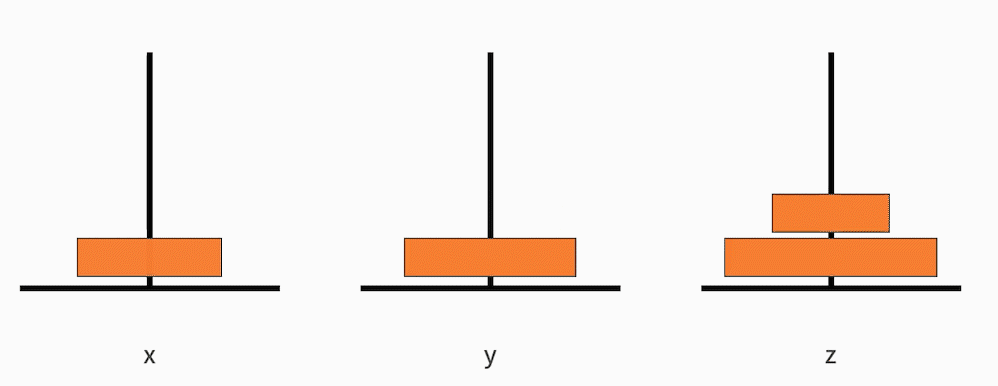
-
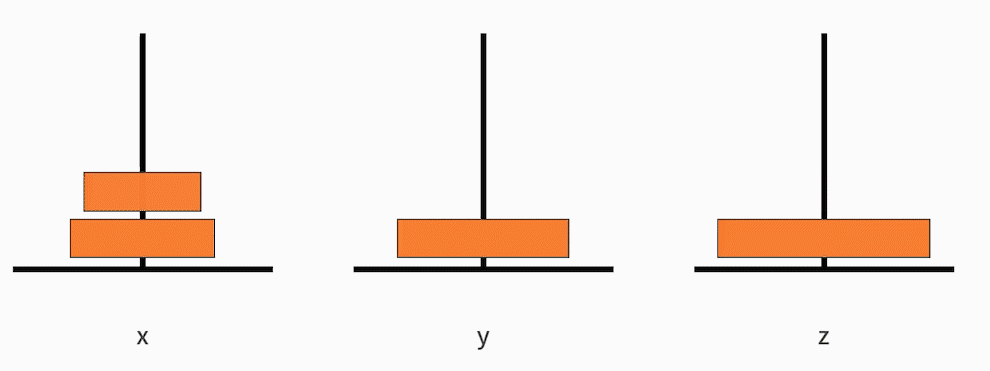
-
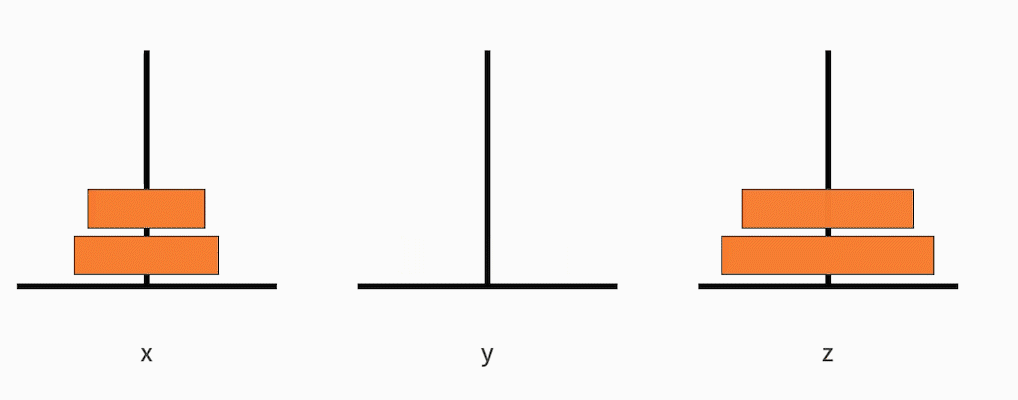
-
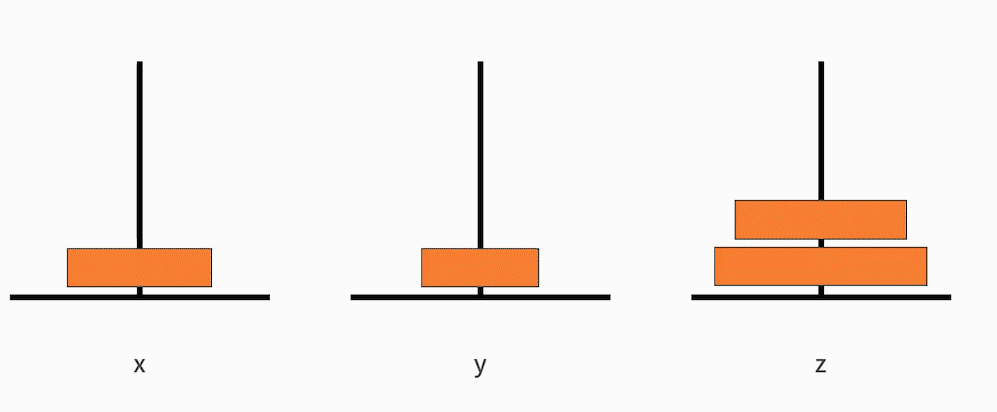
-
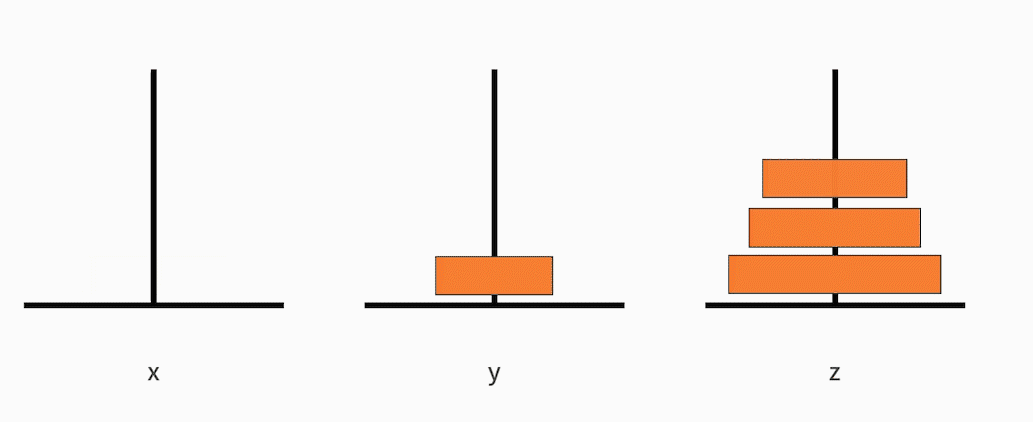
-
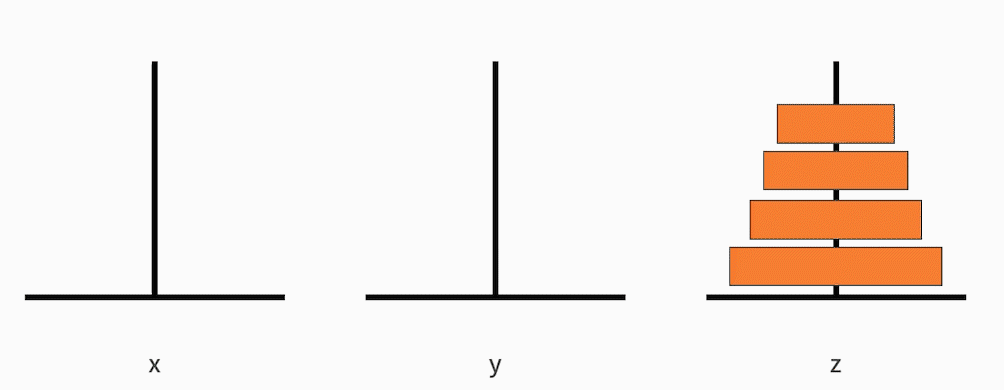
-
判断它是否满足终止条件。随着递归体不断缩小范围,汉诺塔问题由原来“移动从小到大的 n 个盘子”,缩小为“移动从小到大的 n-1 个盘子”,直到缩小为“移动从小到大的 1 个盘子”。
-
移动从小到大的 1 个盘子,就是移动最小的那个盘子。根据规则可以发现,最小的盘子是可以自由移动的。
-
因此,递归的第二个条件,终止条件,也是满足的。
/**
* 汉诺塔问题:
* 从左到右有 x、y、z 三根柱子,其中 x 柱子上面有从小叠到大的 n 个圆盘。
* 现要求将 x 柱子上的圆盘移到 z 柱子上去。要求是,每次只能移动一个盘子,且大盘子不能被放在小盘子上面。求移动的步骤。
* <p>
* hanio(n, x, y, z),代表了把 n 个盘子由 x 移动到 z。
* 把从小到大的 n-1 个盘子从 x 移动到 y,那么代码就是 hanio(n-1, x, z, y);
* 再把最大的一个盘子从 x 移动到 z,那么直接完成一次移动的动作就可以了;
* 再把从小到大的 n-1 个盘子从 y 移动到 z,那么代码就是 hanio(n-1, y, x, z)。
* 终止条件则需要判断 n 的大小。如果 n 等于 1,那么同样直接移动就可以了。
*
* @param n 待移动盘子的数量
* @param x 柱子 x
* @param y 柱子 y
* @param z 柱子 z
*/
public static void hanio(int n, String x, String y, String z) {
if (n < 1) {
System.out.println("汉诺塔的层数不能小于1");
} else if (n == 1) {
System.out.println("移动: " + x + " -> " + z);
return;
} else {
hanio(n - 1, x, z, y);
System.out.println("移动:" + x + " -> " + z);
hanio(n - 1, y, x, z);
}
}
-
以 n = 3 为例,执行上面的代码:
-
在主函数中,执行了 hanio(3, "x", "y", "z")。发现 3 比 1 要大,则进入递归体。分别先后执行了 hanio(2, "x", "z", "y")、"移动: x->z"、hanio(2, "y", "x", "z")。
-
其中的 hanio(2, "x", "z", "y"),又先后执行了 hanio(1, "x", "y", "z")、"移动: x->y"、hanio(1, "z", "x", "y")。在这里,hanio(1, "x", "y", "z") 的执行结果是 "移动: x->z",hanio(1, "z", "x", "y")的执行结果是"移动: z->y"。
-
另一边,hanio(2, "y", "x", "z") 则要先后执行 hanio(1, "y", "z", "x")、"移动: y->z"、hanio(1, "x", "y", "z")。在这里,hanio(1, "y", "z", "x") 的执行结果是"移动: y->x",hanio(1, "x", "y", "z") 的执行结果是 "移动: x->z"。
-





