七、基本数据结构（树形结构）

一、数的概念 Tree

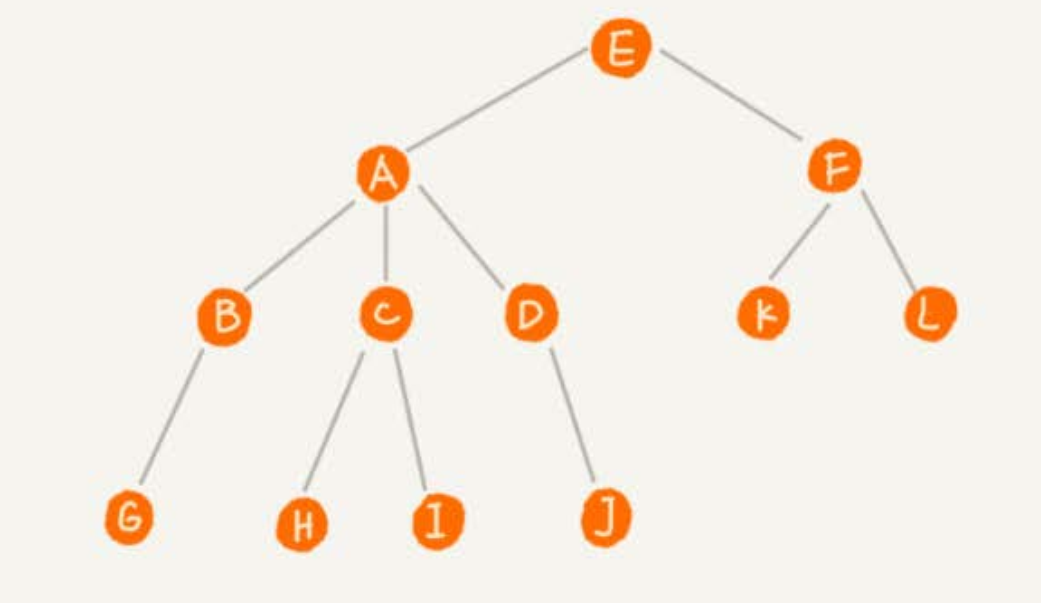
• 如上图所示，是一个树形机构，这里面每个元素叫作“节点”，用来连线相邻节点之间的关系，叫作“父子关系”。
• A 节点是 B 节点的父节点， B 节点是 A 节点的子节点。
• B、 C、 D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。
• 没有父节点的节点叫作根节点，也就是图中的节点 E。
• 我们把没有子节点的节点叫作叶子节点或者叶节点，比如图中的 G、 H、 I、 J、 K、 L 都是叶子节点。
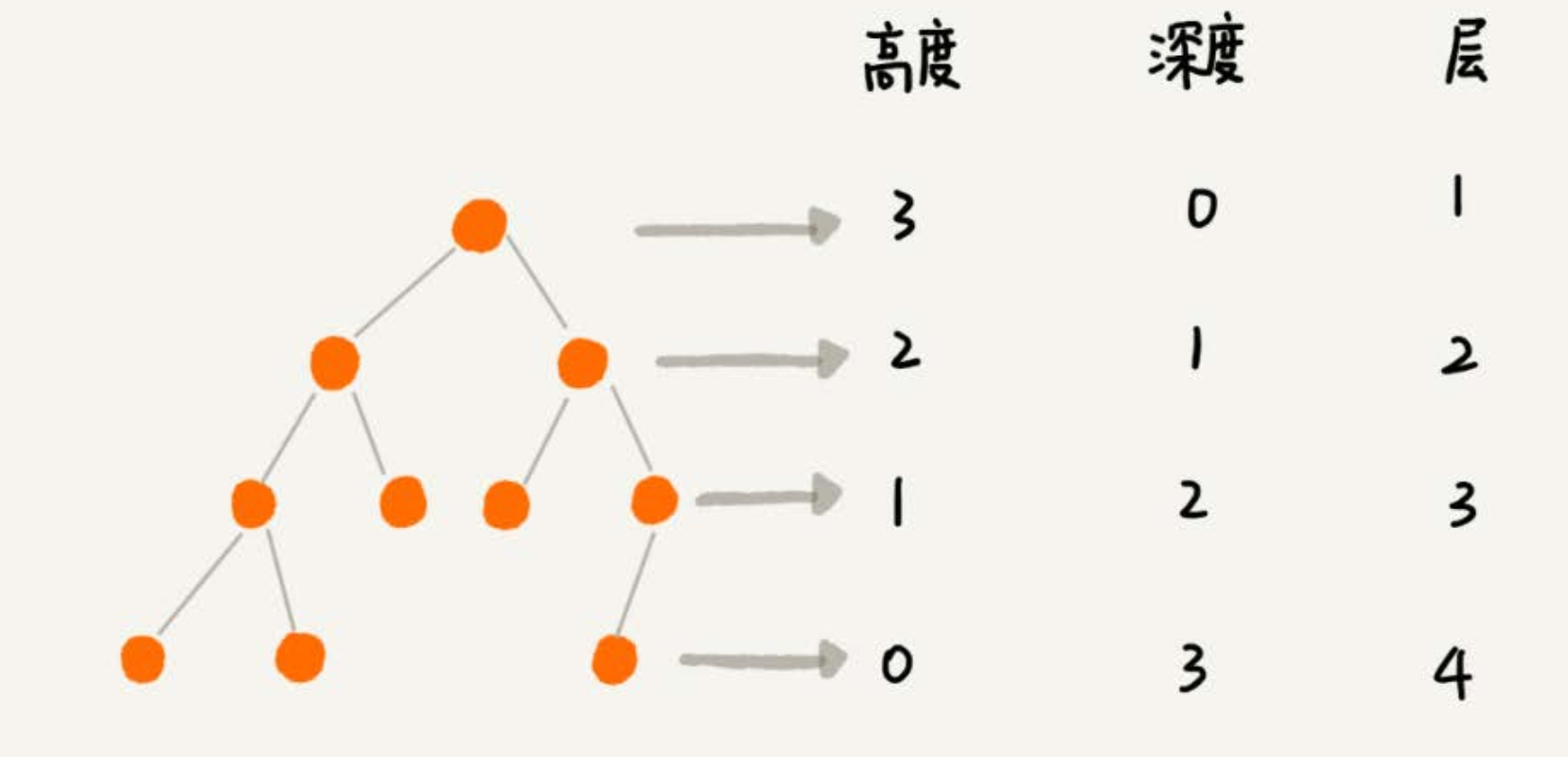
• 节点的高度：节点到叶子节点的最长路径（边数）。
• 节点的深度：根节点到这个节点所经历的边的个数。
• 节点的层数：节点的深度 + 1.
• 树的高度：就是根节点的高度。
• 

二、二叉树

2.1、二叉树介绍

• 二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。

• 不过，二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。

• 

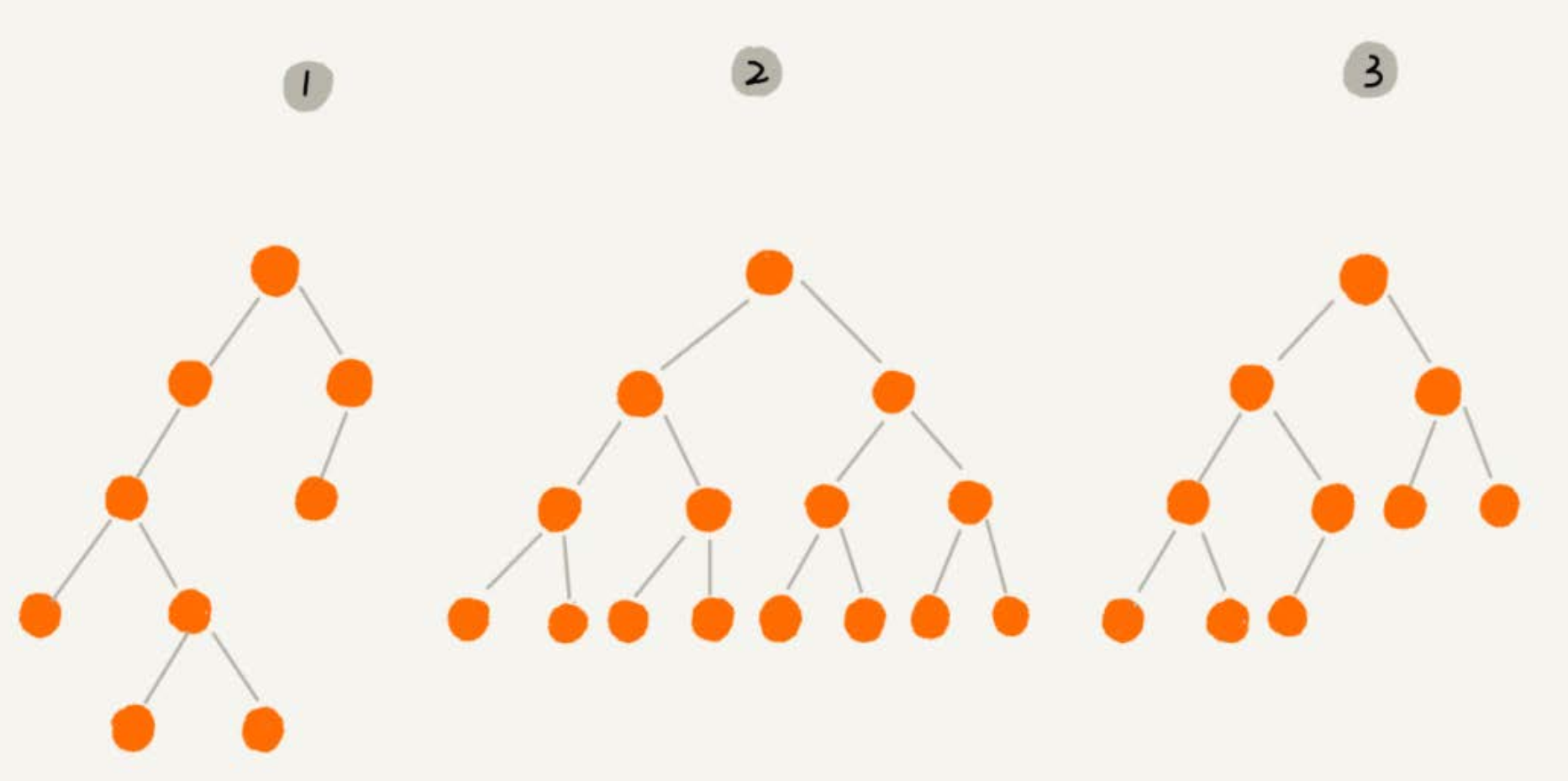
• 编号2的二叉树中，叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。

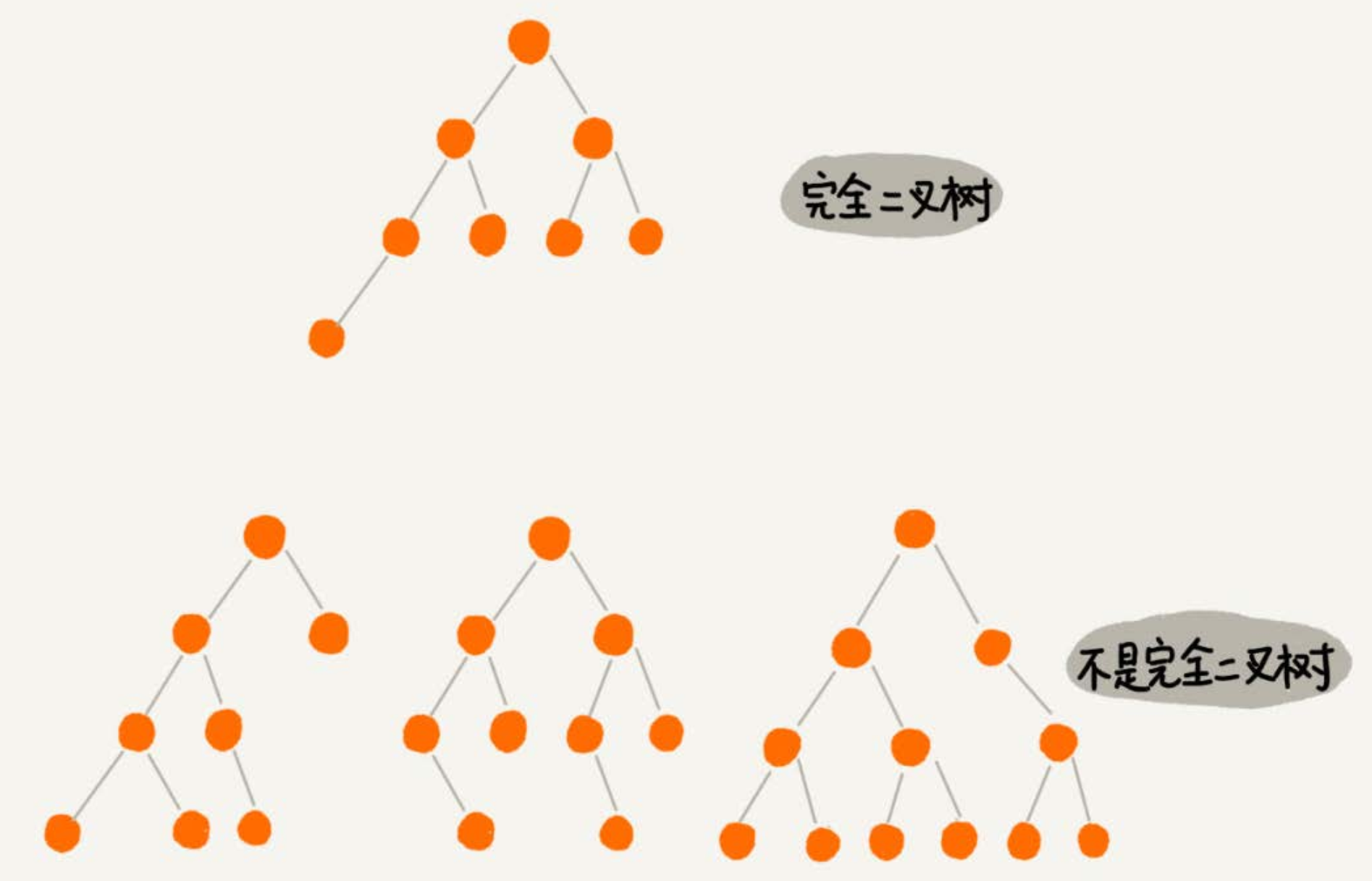
• 编号3的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。

• 

2.2、二叉树的存储

存储一棵二叉树，有两种方法，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。

1.链式存储法

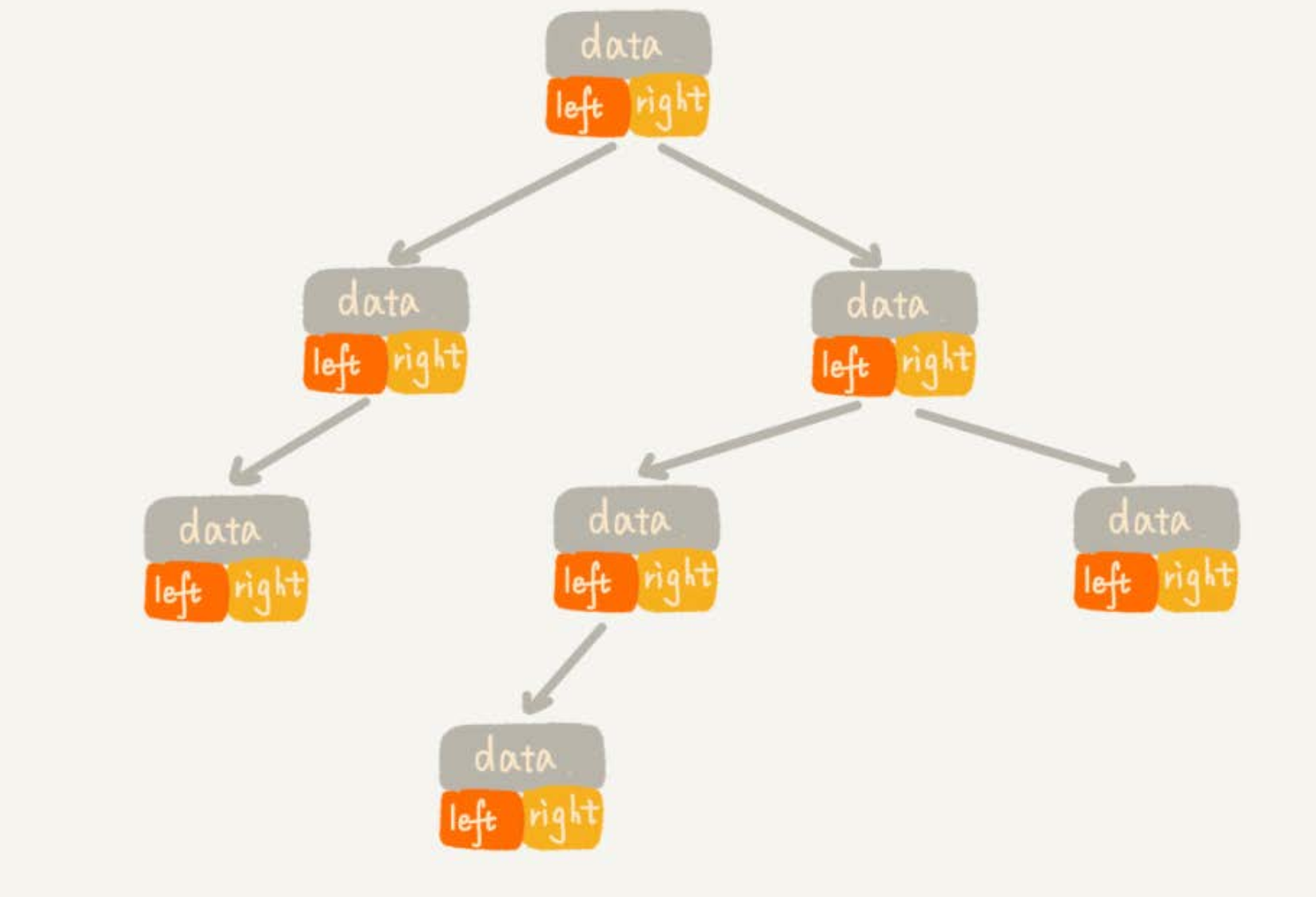
• 链式存储比较简单、直观。
• 如下图所示，每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。
• 只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来。
• 这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。
• 

2.基于数组的顺序存储

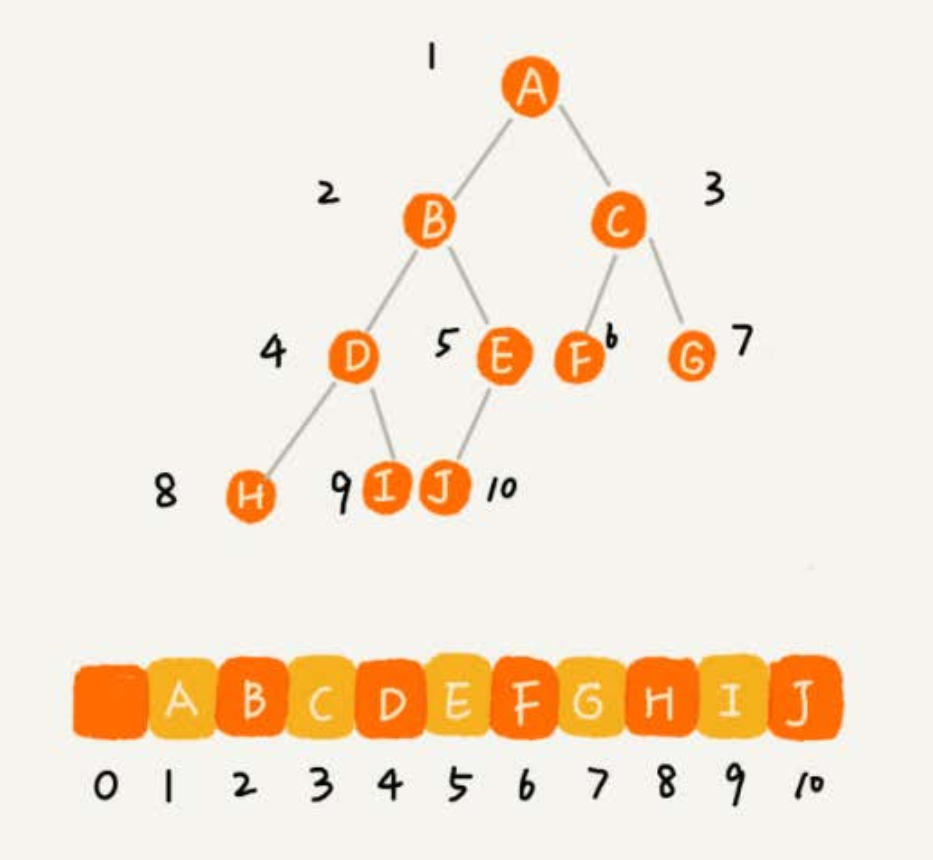
• 如下图所示，把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 * i = 2 的位置，右子节点存储在 2 * i + 1 = 3 的位置。

• 以此类推， B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。

• 

• 如果节点 X 存储在数组中下标为 i 的位置，下标为 2 * i 的位置存储的就是左子节点，下标为 2 * i + 1 的位置存储的就是右子节点。

• 反过来，下标为 i/2 的位置存储就是它的父节点。

• 通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为1的位置），这样就可以通过下标计算，把整棵树都串起来。

2.3。二叉树的遍历

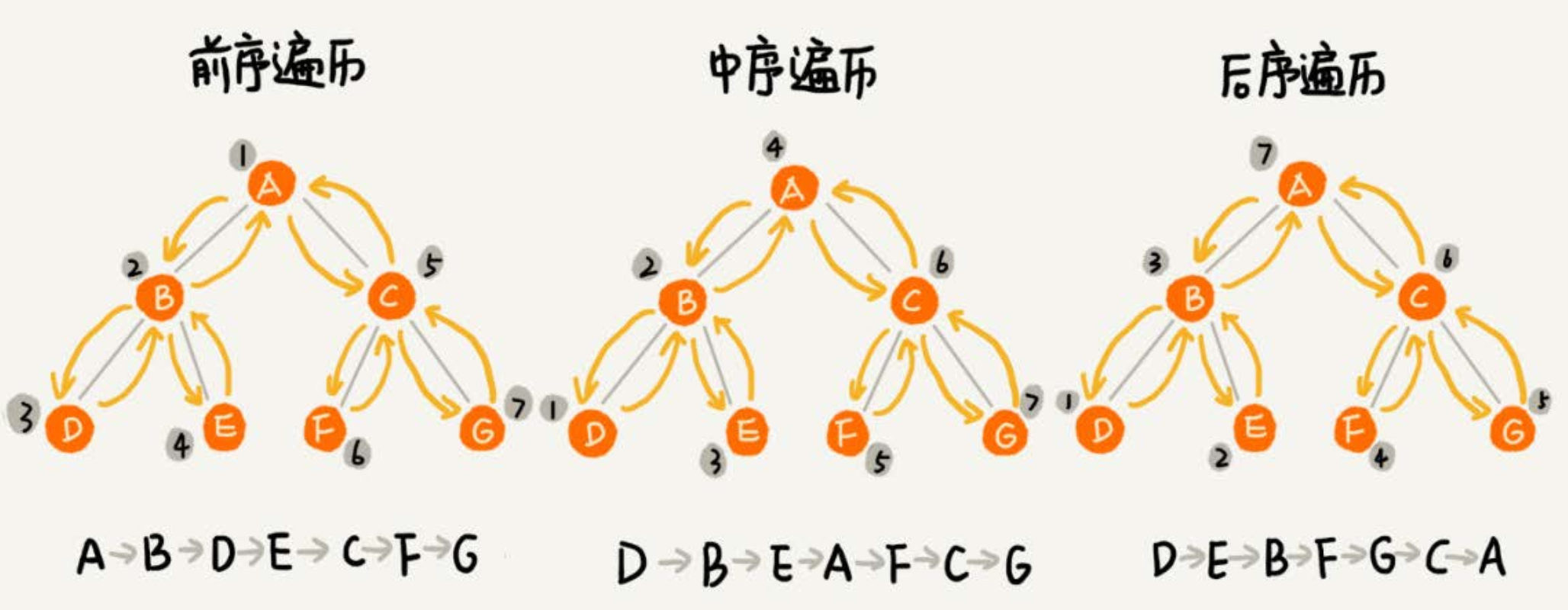
• 前序遍历：对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。

• 中序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。

• 后序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

• 

• 实际上，二叉树的前、中、后序遍历就是一个递归的过程。

• 比如，前序遍历，其实就是先打印根节点，然后再递归地打印左子树，最后递归地打印右子树。

• 前序遍历的递推公式：preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)。

• 中序遍历的递推公式：inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

• 后序遍历的递推公式：postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

• 从上面的前、中、后序遍历的顺序图，可以看出来，每个节点最多会被访问两次，所以遍历操作的时间复杂度，跟节点的个数 n 成正比，也就是说二叉树遍历的时间复杂度是 O(n)。

static class Node {
    Node rightNode;
    Node leftNode;
    String data;
}

/**
 * 先序遍历，先打印本身，在打印左节点，在打印右节点
 *
 * @param node
 */
public static void preOrderTraverse(Node node) {
    if (node == null) {
        return;
    }
    System.out.print(node.data + " ");
    preOrderTraverse(node.leftNode);
    preOrderTraverse(node.rightNode);
}

/**
 * 中序遍历，先打印左节点，在打印本身，在打印右节点
 *
 * @param node
 */
public static void inOrderTraverse(Node node) {
    if (node == null) {
        return;
    }
    inOrderTraverse(node.leftNode);
    System.out.print(node.data + " ");
    inOrderTraverse(node.rightNode);
}

/**
 * 后序遍历，先打印左节点，在打印右节点，在打印自己
 *
 * @param node
 */
public static void postOrderTraverse(Node node) {
    if (node == null) {
        return;
    }
    preOrderTraverse(node.rightNode);
    preOrderTraverse(node.leftNode);
    System.out.print(node.data + " ");

}

/**
 * 数的层级遍历
 *
 * @param root
 */
public static void levelTraverse(Node root) {
    if (root == null) {
        return;
    }

    LinkedList<Node> queue = new LinkedList<Node>();
    Node current = null;
    // 根节点入队
    queue.offer(root);

    // 左侧数的深度
    int leftNum = 0;
    // 右侧数的深度
    int rightNum = 0;

    // 只要队列中有元素，就可以一直执行，非常巧妙地利用了队列的特性
    while (!queue.isEmpty()) {
        // 出队队头元素
        current = queue.poll();
        System.out.print("-->" + current.data);
        // 左子树不为空，入队
        if (current.leftNode != null) {
            queue.offer(current.leftNode);
            leftNum++;
        }

        // 右子树不为空，入队
        if (current.rightNode != null) {
            queue.offer(current.rightNode);
            rightNum++;
        }
    }
    System.out.println(rightNum + "\t" + leftNum);
}

三、二叉查找树（Binary Search Tree）

• 二叉查找树是二叉树中最常用的一种类型，也叫二叉搜索树。
• 二叉查找树是为了实现快速查找而生的。
• 它不仅仅支持快速查找一个数据，还支持快速插入、删除一个数据。
• 二叉查找树要求，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。
• 二叉查找树最大的特点就是，支持动态数据集合的快速插入、删除、查找操作。
• 中序遍历二叉查找树，可以输出有序的数据序列，时间复杂度是 O(n)，非常高效。
• 

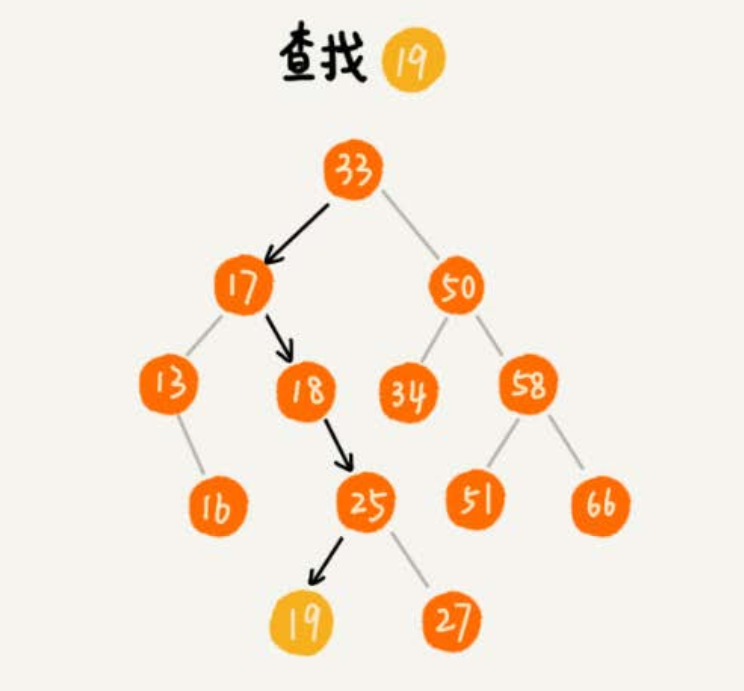
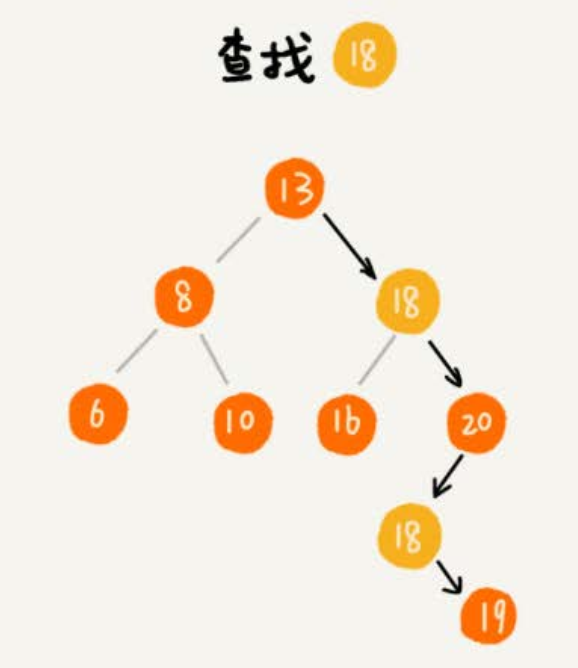
3.1、二叉查找树的查找操作

• 先取根节点，如果它等于要查找的数据，就返回。
• 如果要查找的数据比根节点的值小，那就在左子树中递归查找；
• 如果要查找的数据比根节点的值大，那就在右子树中递归查找。
• 

public class BinarySearchTree {

    private Node tree;

    public Node find(int data) {
        Node p = tree;
        while (p != null) {
            if (data < p.data) p = p.leftNode;
            else if (data > p.data) p = p.rightNode;
            else return p;
        }
        return null;
    }


    class Node {
        private int data;
        private Node leftNode;
        private Node rightNode;

        public Node(int data) {
            this.data = data;
        }
    }
}

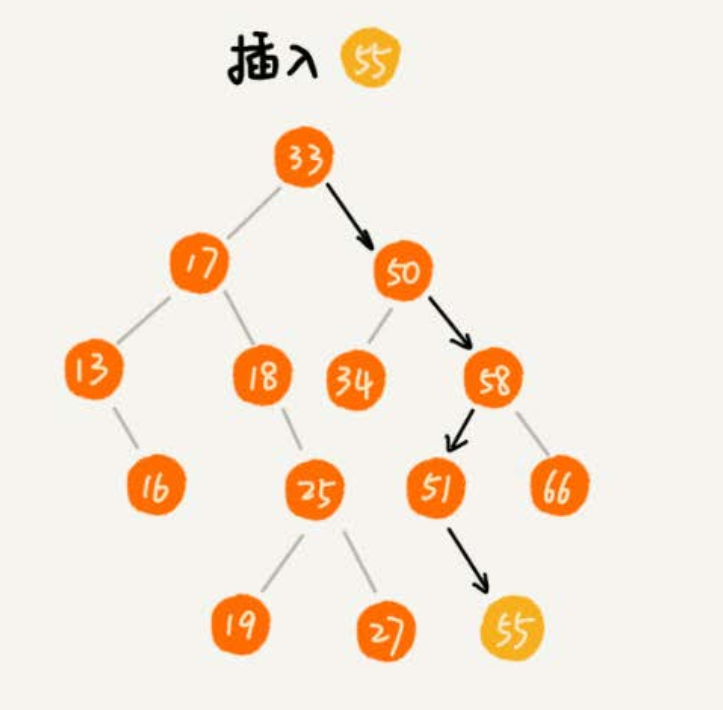
3.2、二叉查找树的插入操作

• 二叉查找树的插入过程有点类似查找操作。
• 新插入的数据一般都是在叶子节点上，所以只需要从根节点开始，依次比较要插入的数据和节点的大小关系。
• 如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；
• 如果不为空，就再递归遍历右子树，查找插入位置。
• 同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。
  

/**
 * 插入操作
 *
 * @param data
 * @return
 */
public Boolean insert(int data) {
    if (tree == null) {
        tree = new Node(data);
        return true;
    }
    Node p = tree;
    while (p != null) {
        if (data > p.data) {
            // 插入右节点
            if (p.rightNode == null) {
                p.rightNode = new Node(data);
                return true;
            }
            p = p.rightNode;
        } else {
            // 插入 左节点
            if (p.leftNode == null) {
                p.leftNode = new Node(data);
                return true;
            }
            p = p.leftNode;
        }
    }
    return false;
}

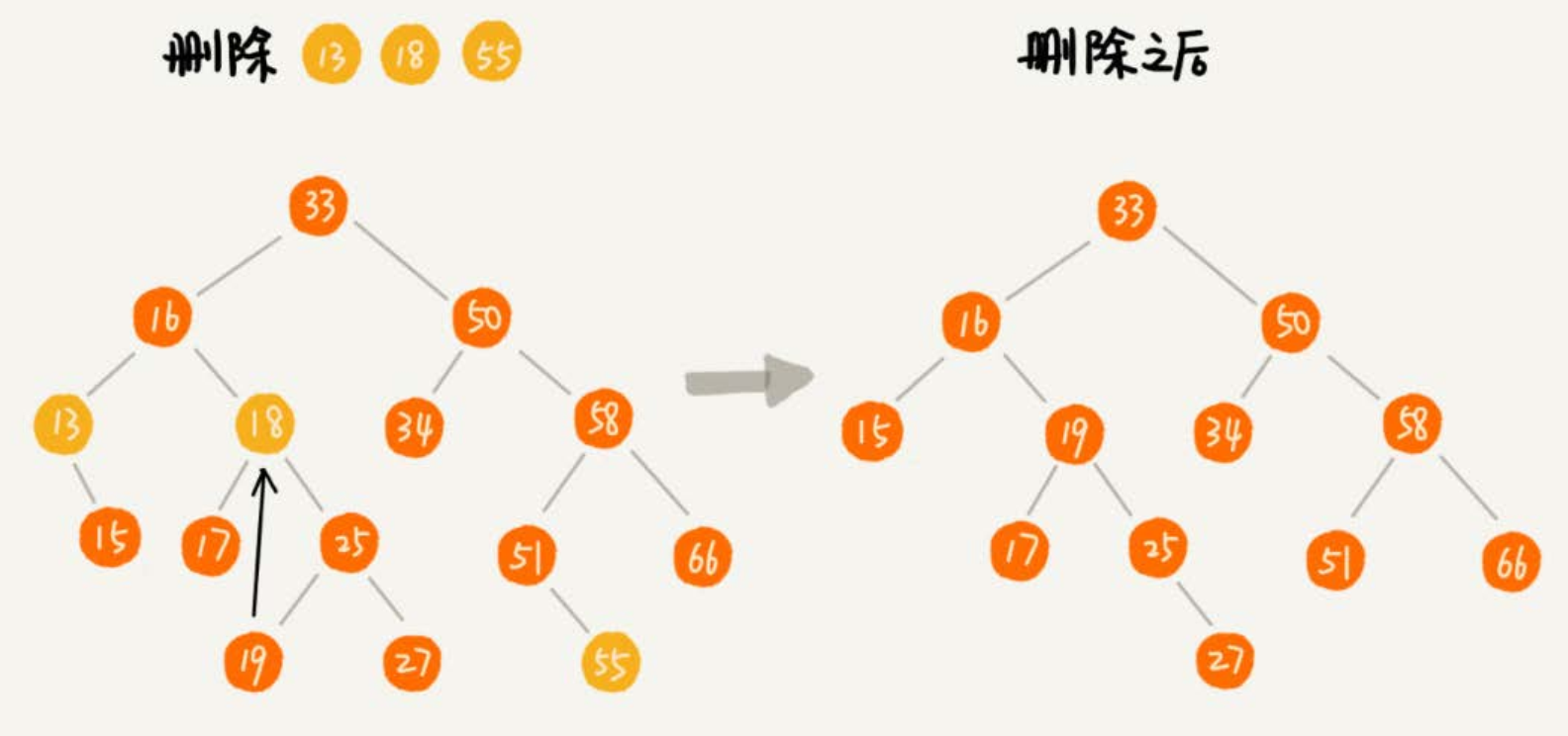
3.3、二叉查找树的删除操作

• 针对要删除节点的子节点个数的不同，需要分三种情况来处理。
• 第一种情况是，如果要删除的节点没有子节点
  • 只需要直接将父节点中，指向要删除节点的指针置为 null。
  • 比如图中的删除节点 55。
• 第二种情况是，如果要删除的节点只有一个子节点（只有左子节点或者右子节点）
  • 只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。
  • 比如图中的删除节点 13。
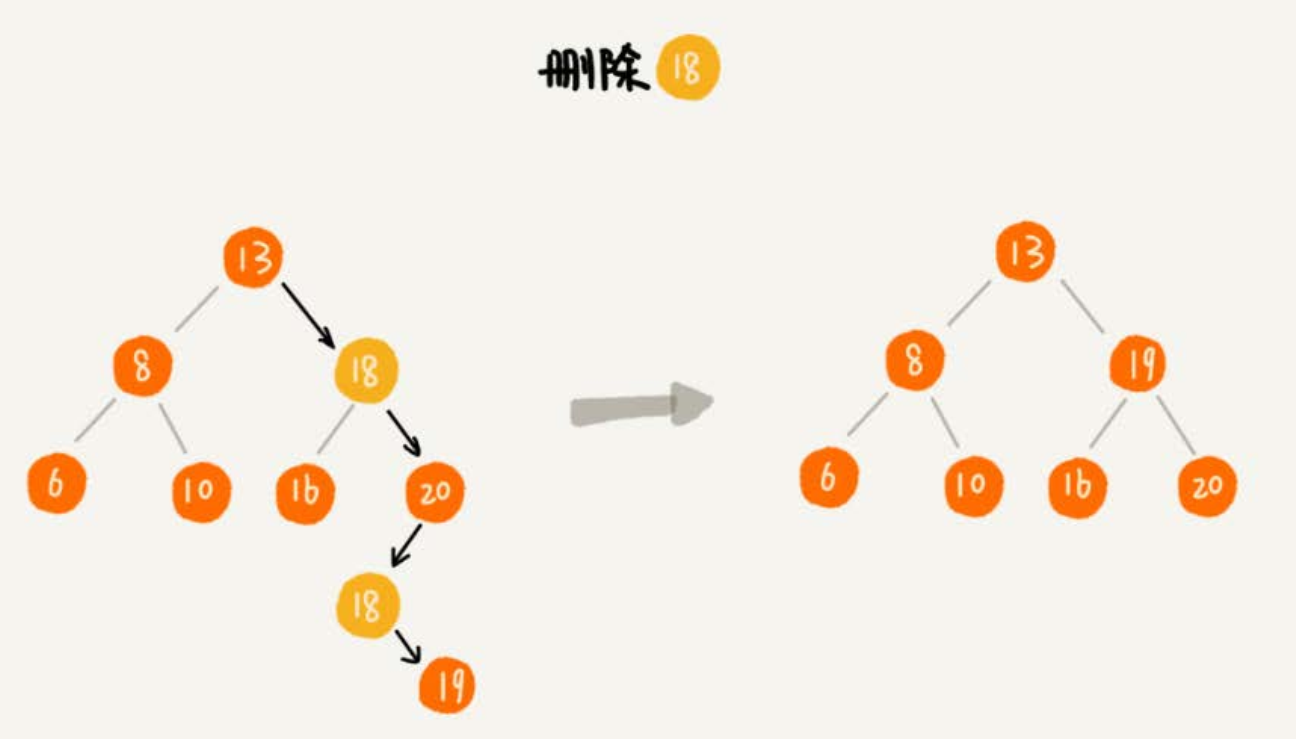
• 第三种情况是，如果要删除的节点有两个子节点
  • 需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。
  • 然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了）。
  • 所以，可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。
• 

/**
 * 删除
 * @param data
 */
public void delete(int data) {
    // p指向要删除的节点，初始化指向根节点
    Node p = tree;
    // pp记录的是p的父节点
    Node pp = null;

    // 查找要删除的节点位置，及其父节点
    while (p != null && p.data != data) {
        pp = p;
        if (data > p.data) {
            p = p.rightNode;
        } else {
            p = p.leftNode;
        }
    }
    if (p == null) {
        return;// 没有找到
    }
    // 要删除的节点有两个子节点
    if (p.leftNode != null && p.rightNode != null) {
        // 查找右子树中最小节点
        Node minp = p.rightNode;
        Node minpp = p; // minPP表示minP的父节点
        while (minp.leftNode != null) {
            minpp = minp;
            minp = minp.leftNode;
        }
        // 将 minp 的数据替换到 p 中
        p.data = minp.data;
        // 下面就变成了删除 minp 了
        p = minp;
        pp = minpp;
    }
    // 删除节点是叶子节点或者仅有一个子节点
    Node child; // p 的子节点
    if (p.leftNode != null) {
        child = p.leftNode;
    } else if (p.rightNode != null) {
        child = p.rightNode;
    } else {
        child = null;
    }
    if (pp == null) {
        // 删除的是根节点
        tree = child;
    } else if (pp.leftNode == p) {
        pp.leftNode = child;
    } else {
        pp.rightNode = child;
    }
}

• 实际上，关于二叉查找树的删除操作，还有个非常简单、取巧的方法，就是单纯将要删除的节点标记为“已删除”，但是并不真正从树中将这个节点去掉。
• 这样原本删除的节点还需要存储在内存中，比较浪费内存空间，但是删除操作就变得简单了很多。
• 而且，这种处理方法也并没有增加插入、查找操作代码实现的难度。

3.4、支持重复数据的二叉查找树

• 上文提到的二叉查找树，默认树中节点存储的都是数字。很多时候，在二叉查找树中存储的，是一个包含很多字段的对象。
• 利用对象的某个字段作为键值（key）来构建二叉查找树。把对象中的其他字段叫作卫星数据。
• 前面讲的二叉查找树的操作，针对的都是不存在键值相同的情况。
• 那如果存储的两个对象键值相同，解决方法如下：

  • 第一种方法比较容易。二叉查找树中每一个节点不仅会存储一个数据，因此通过链表和支持动态扩容的数组等数据结构，把值相同的数据都存储在同一个节
    点上。

  • 第二种方法是，每个节点仍然只存储一个数据。

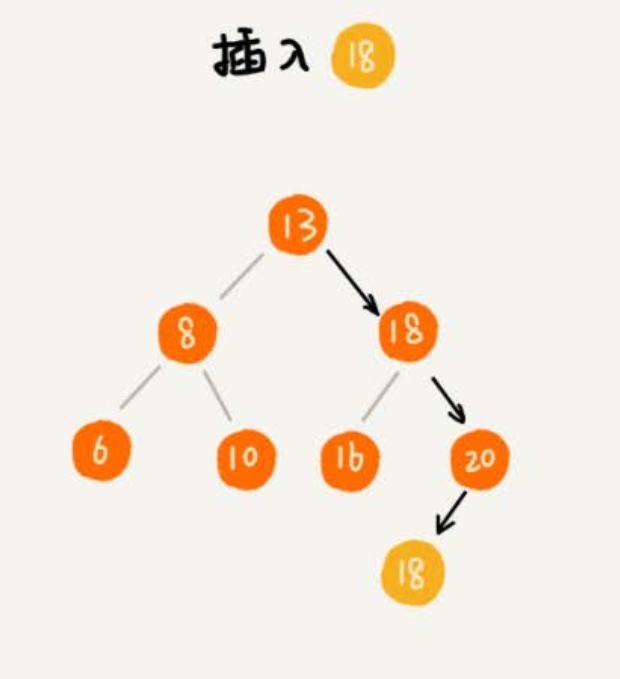
  • 在查找插入位置的过程中，如果碰到一个节点的值，与要插入数据的值相同，就将这个要插入的数据放到这个节点的右子树，也就是说，把这个新插入的数据当作大于这个节点的值来处理。

  • 

  • 当要查找数据的时候，遇到值相同的节点，并不停止查找操作，而是继续在右子树中查找，直到遇到叶子节点，才停止。这样就可以把键值等于要查找值的所有节点都找出来。

  • 

  • 对于删除操作，也需要先查找到每个要删除的节点，然后再按前面讲的删除操作的方法，依次删除。

  • 

3.5、二叉查找树的时间复杂度分析

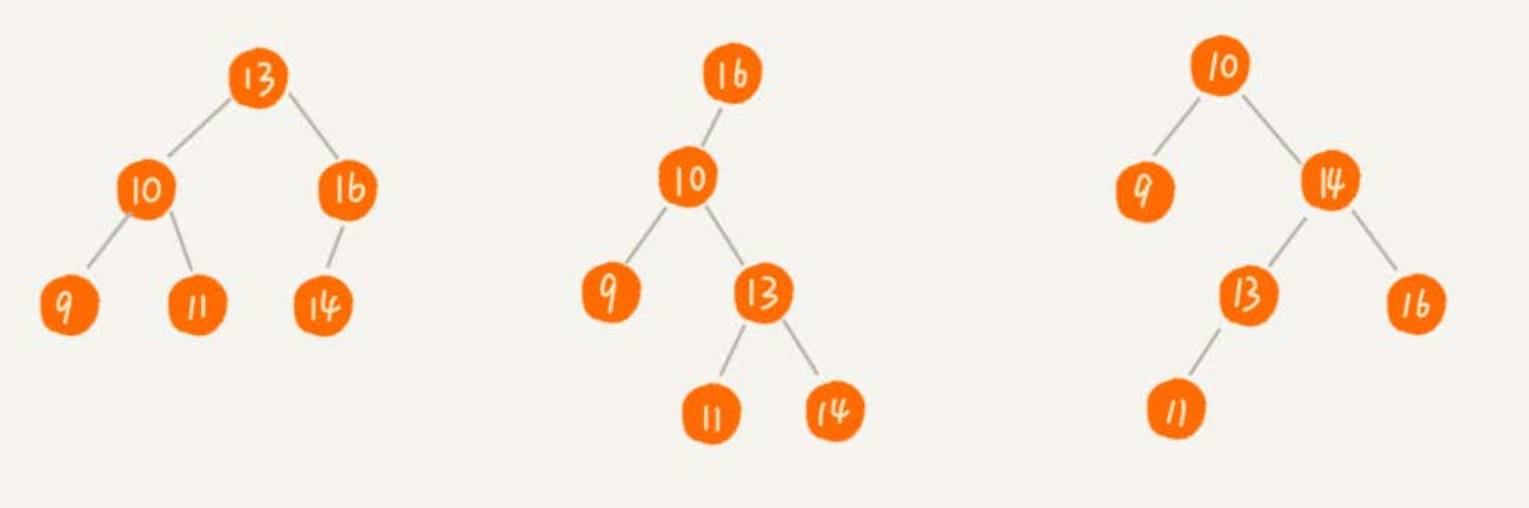
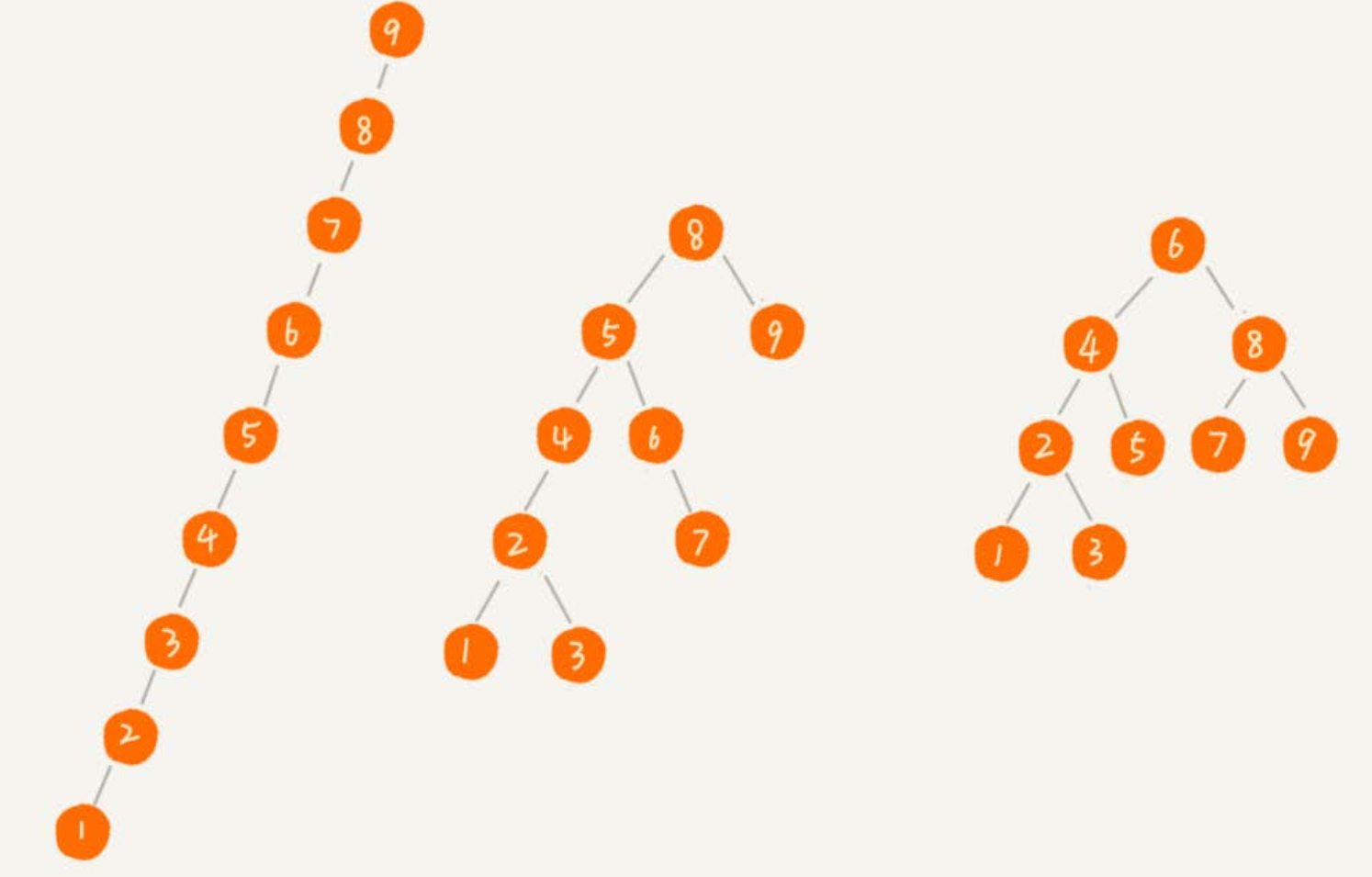
• 二叉查找树的形态各式各样。如下图所示，对于同一组数据，构造了三种二叉查找树。它们的查找、插入、删除操作的执行效率都是不一样的。

• 图中第一种二叉查找树，根节点的左右子树极度不平衡，已经退化成了链表，所以查找的时间复杂度就变成了 O(n)。

• 

• 从前面的例子、图，以及还有代码来看，不管操作是插入、删除还是查找， 时间复杂度其实都跟树的高度成正比，也就是 O(height)。

• 既然这样，现在问题就转变成另外一个了，也就是，如何求一棵包含 n 个节点的完全二叉树的高度？

• 树的高度就等于最大层数减一，为了方便计算，转换成层来表示。

• 从图中可以看出，包含 n 个节点的完全二叉树中，第一层包含1个节点，第二层包含2个节点，第三层包含4个节点，依次类推，下面一层节点个数是上一层的 2 倍，第 K 层包含的节点个数就是 2^(K-1)。

• 不过，对于完全二叉树来说，最后一层的节点个数有点儿不遵守上面的规律了。它包含的节点个数在 1 个到 2^(L-1) 个之间（假设最大层数是L）。

• 如果我们把每一层的节点个数加起来就是总的节点个数 n。也就是说，如果节点的个数是 n，那么 n 满足这样一个关系：

• n >= 1+2+4+8+...+2^(L-2)+1

• n <= 1+2+4+8+...+2^(L-2)+2(L-1)

• 借助等比数列的求和公式，我们可以计算出，L 的范围是 [log2(n+1), log2n +1]。完全二叉树的层数小于等于 log2n +1，也就是说，完全二叉树的高度小于等于 log2n。

• 显然，极度不平衡的二叉查找树，它的查找性能肯定不能满足需求。

• 需要构建一种不管怎么删除、插入数据，在任何时候，都能保持任意节点左右子树都比较平衡的二叉查找树，这就是平衡二叉查找树。

• 平衡二叉查找树的高度接近 logn，所以插入、删除、查找操作的时间复杂度也比较稳定，是 O(logn)。

四、红黑树

• 二叉查找树是最常用的一种二叉树，它支持快速插入、删除、查找操作，各个操作的时间复杂度跟树的高度成正比，理想情况下，时间复杂度是 O(logn)。
• 不过，二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于 log2n 的情况，从而导致各个操作的效率下降。
• 极端情况下，二叉树会退化为链表，时间复杂度会退化到 O(n)。
• 要解决这个复杂度退化的问题，需要设计一种平衡二叉查找树，比如红黑树。

4.1、平衡二叉查找树

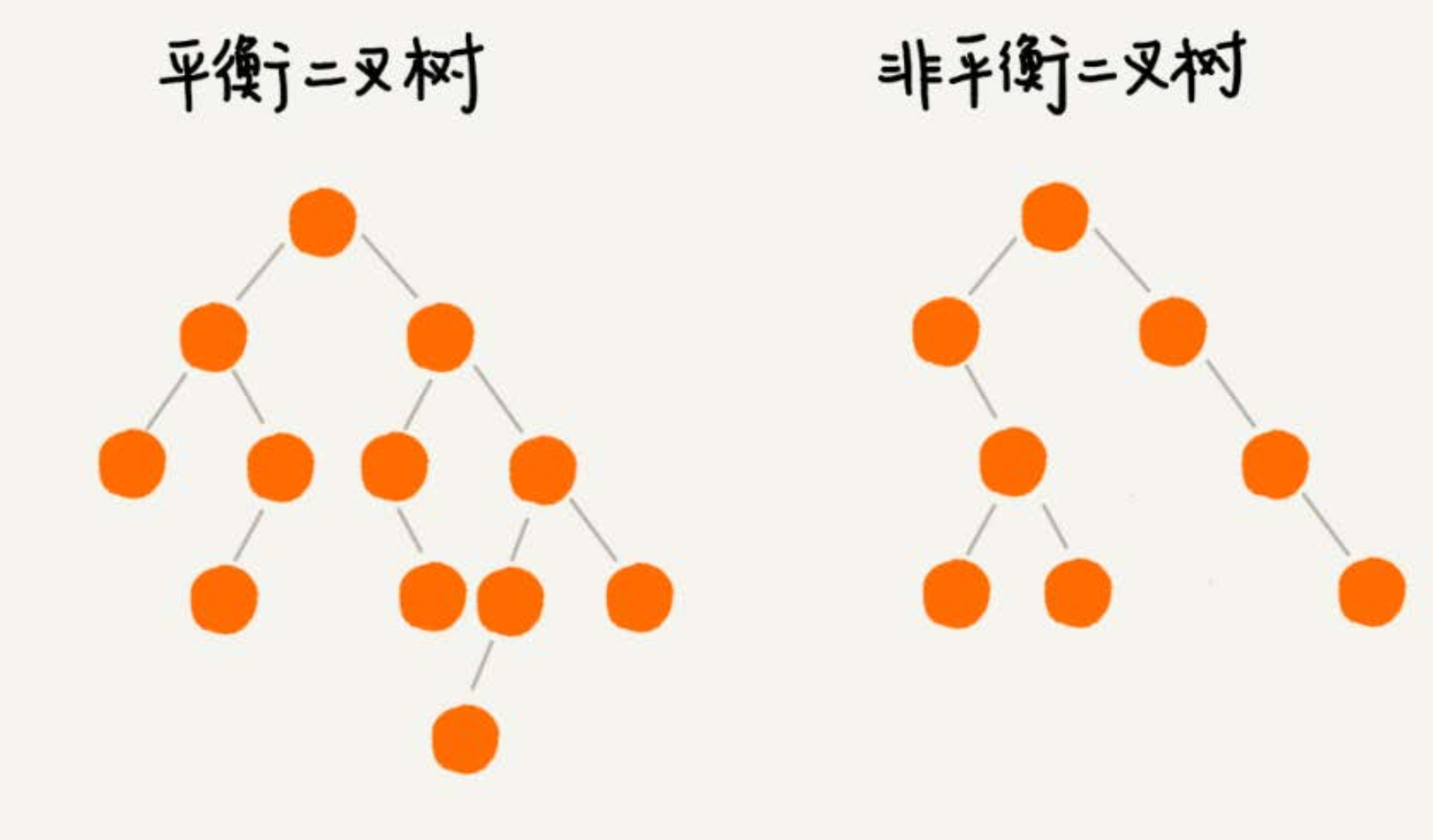
• 平衡二叉树的严格定义是这样的：二叉树中任意一个节点的左右子树的高度相差不能大于 1。

• 从这个定义来看，完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。

• 

• 平衡二叉查找树不仅满足上面平衡二叉树的定义，还满足二叉查找树的特点。

• 最先被发明的平衡二叉查找树是 AVL 树，它严格符合刚讲到的平衡二叉查找树的定义，即任何节点的左右子树高度相差不超过 1，是一种高度平衡的二叉查找树。

• 但是很多平衡二叉查找树其实并没有严格符合上面的定义（树中任意一个节点的左右子树的高度相差不能大于1），比如红黑树，它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。

• 发明平衡二叉查找树这类数据结构的初衷是，解决普通二叉查找树在频繁的插入、删除等动态更新的情况下，出现时间复杂度退化的问题。

• 所以， 平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。

• 这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

• 所以，如果现在设计一个新的平衡二叉查找树，只要树的高度不比 log2n 大很多（比如树的高度仍然是对数量级的），尽管它不符合严格的平衡二叉查找树的定义，但仍然可以说，这是一个合格的平衡二叉查找树。

4.2、红黑树

• 平衡二叉查找树其实有很多，比如， Splay Tree（伸展树）、 Treap（树堆）等，但是提到平衡二叉查找树，听到的基本都是红黑树。
• 他的出镜率甚至要高于“平衡二叉查找树”这几个字，有时候，甚至默认平衡二叉查找树就是红黑树。
• 红黑树的英文是“Red-Black Tree”，简称R-B Tree。它是一种不严格的平衡二叉查找树，它的定义是不严格符合平衡二叉查找树的定义的。
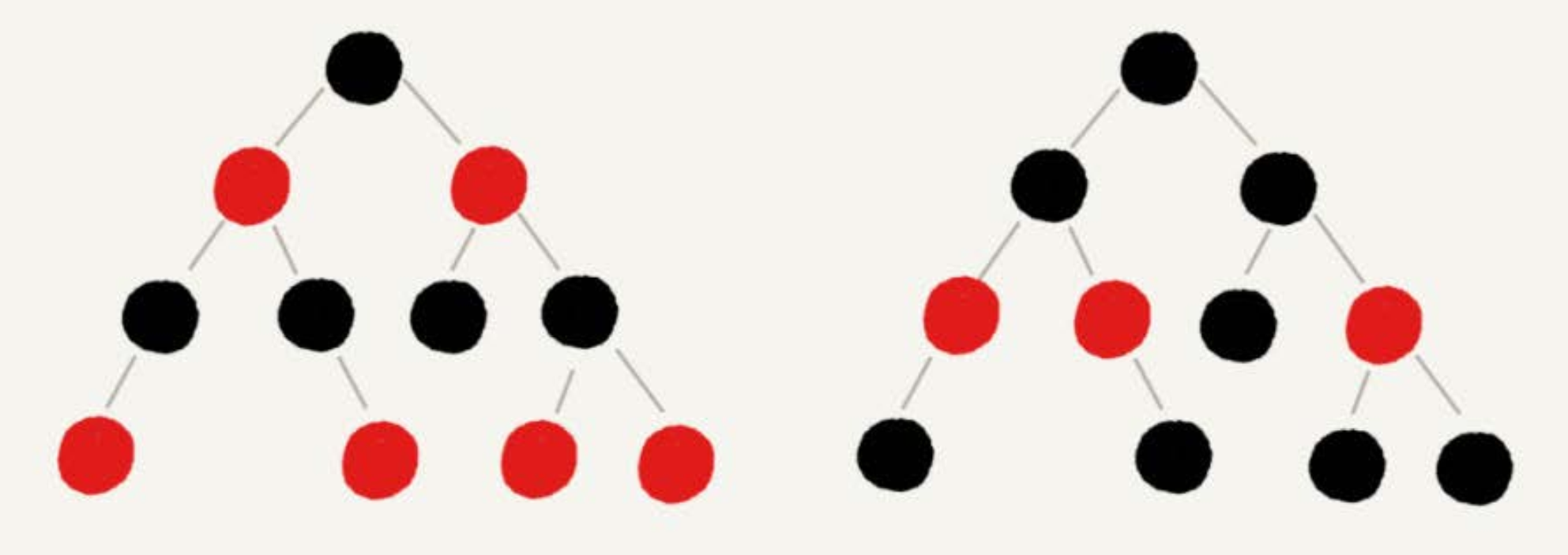
• 顾名思义，红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：
  • 根节点是黑色的；
  • 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
  • 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
  • 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；
  • 这里的第二点要求“叶子节点都是黑色的空节点”，它主要是为了简化红黑树的代码实现而设置的。
  • 下图中将黑色的、空的叶子节点都省略掉了。
  • 

1.为什么说红黑树是“近似平衡”的？

• 平衡二叉查找树的初衷，是为了解决二叉查找树因为动态更新导致的性能退化问题。所以，“平衡”的意思可以等价为性能不退化。

• “近似平衡”就等价为性能不会退化的太严重。

• 二叉查找树很多操作的性能都跟树的高度成正比。

• 一棵极其平衡的二叉树（满二叉树或完全二叉树）的高度大约是 log2n，所以如果要证明红黑树是近似平衡的，只需要分析，红黑树的高度是否比较稳定地趋近 log2n 就好了。

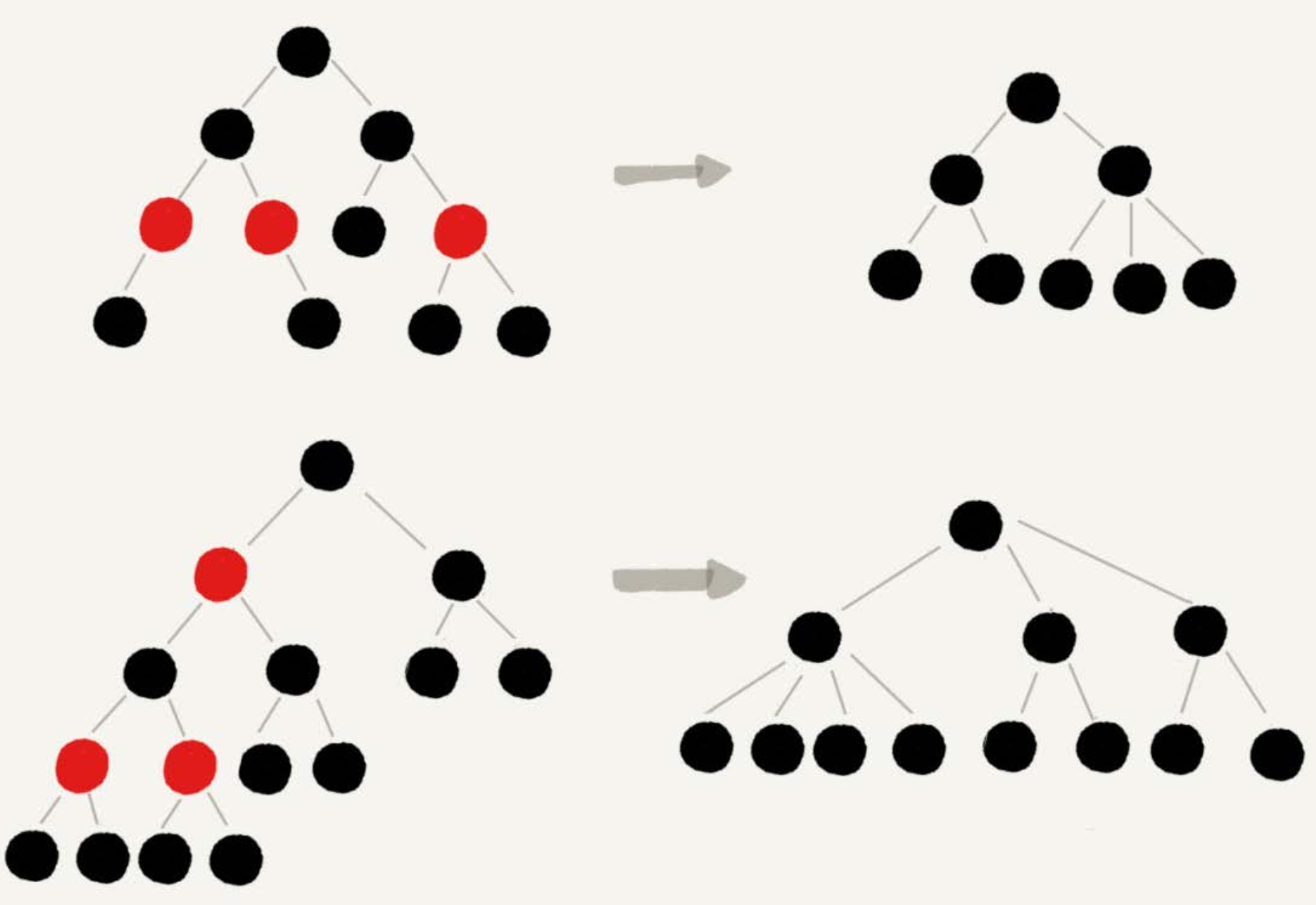
• 如果将红色节点从红黑树中去掉，那单纯包含黑色节点的红黑树的高度是多少呢？

• 红色节点删除之后，有些节点就没有父节点了，它们会直接拿这些节点的祖父节点（父节点的父节点）作为父节点。所以，之前的二叉树就变成了四叉树。

• 

• 前面红黑树的定义里有这么一条：从任意节点到可达的叶子节点的每个路径包含相同数目的黑色节点。

• 从四叉树中取出某些节点，放到叶节点位置，四叉树就变成了完全二叉树。所以，仅包含黑色节点的四叉树的高度，比包含相同节点个数的完全二叉树的高度还要小。

• 完全二叉树的高度近似 log2n，这里的四叉“黑树”的高度要低于完全二叉树，所以去掉红色节点的“黑树”的高度也不会超过 log2n。

• 现在知道只包含黑色节点的“黑树”的高度，那我们现在把红色节点加回去，高度会变成多少呢？

• 从上面画的红黑树的例子和定义看，在红黑树中，红色节点不能相邻，也就是说，有一个红色节点就要至少有一个黑色节点，将它跟其他红色节点隔开。

• 红黑树中包含最多黑色节点的路径不会超过l og2n，所以加入红色节点之后，最长路径不会超过 2log2n，也就是说，红黑树的高度近似 2log2n。

• 所以，红黑树的高度只比高度平衡的AVL树的高度（log2n）仅仅大了一倍，在性能上，下降得并不多。

• 这样推导出来的结果不够精确，实际上红黑树的性能更好。