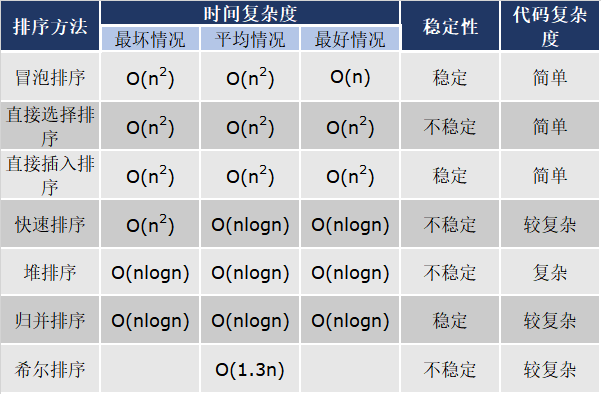
基本排序
什么是递归
简但来说递归的特点就是,能够自己调用自己,就像两块镜子相对而放,一个合格的递归应当拥有:一个入口,一个出口,即限制自己在自己的程序体中调用自己。
评价算法好坏的标准
两个概念:时间复杂度和空间复杂度(代码是否容易实现)
时间复杂度:用于体现算法执行时间的快慢,用O表示。一般常用的有:几次循环就为O(n几次方) 循环减半的O(logn)
空间复杂度:用来评估算法内存占用大小的一个式子,通常情况下会选择使用空间换时间
查找算法
列表查找:从列表中查找指定元素
输入:列表、待查找元素
输出:元素下标或未查找到元素
顺序查找:从列表中的第一个元素开始,顺序进行搜索,直到找到为止,复杂度为O(n)
二分查找:从有序列表中,通过待查值与中间值比较,以减半的方式进行查找,复杂度为O(logn)
代码如下:
list = [1,2,3,4,5,6,7,8,9] element = 7 def ord_sear(list,element): for i in range(0,len(list)): if list[i] == element: print('list[{0}]={1}'.format(i,element)) return i else: print('not found') def bin_sear(list,element): low = 0 high = len(list)-1 while low<=high: mid = (low+high)//2 if element == list[mid]: print('list[{0}]={1}'.format(mid,element)) return mid elif element > list[mid]: low =mid +1 else: high =mid -1 return None i = bin_sear(list,element) j = ord_sear(list,element)
二分查找虽然在时间复杂度上优于顺序查找,但是有比较苛刻的条件,即列表必须为有序的。
在二分查找的基础上进一步扩展的插值查找法其实是一样的思想:
插值算法的总体时间复杂度仍然属于O(log(n))级别的。其优点是,对于表内数据量较大,且关键字分布比较均匀的查找表,使用插值算法的平均性能比二分查找要好得多。反之,对于分布极端不均匀的数据,则不适合使用插值算法。

1 # 插值查找算法 2 # 时间复杂度O(log(n)) 3 4 def binary_search(lis, key): 5 low = 0 6 high = len(lis) - 1 7 time = 0 8 while low < high: 9 time += 1 10 # 计算mid值是插值算法的核心代码 11 mid = low + int((high - low) * (key - lis[low])/(lis[high] - lis[low])) 12 print("mid=%s, low=%s, high=%s" % (mid, low, high)) 13 if key < lis[mid]: 14 high = mid - 1 15 elif key > lis[mid]: 16 low = mid + 1 17 else: 18 # 打印查找的次数 19 print("times: %s" % time) 20 return mid 21 print("times: %s" % time) 22 return False
斐波那契查找
由插值算法带来的启发,发明了斐波那契算法。其核心也是如何优化那个缩减速率,使得查找次数尽量降低。
使用这种算法,前提是已经有一个包含斐波那契数据的列表
F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…]

1 # 斐波那契查找算法 2 # 时间复杂度O(log(n)) 3 4 def fibonacci_search(lis, key): 5 # 需要一个现成的斐波那契列表。其最大元素的值必须超过查找表中元素个数的数值。 6 F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 7 233, 377, 610, 987, 1597, 2584, 4181, 6765, 8 10946, 17711, 28657, 46368] 9 low = 0 10 high = len(lis) - 1 11 12 # 为了使得查找表满足斐波那契特性,在表的最后添加几个同样的值 13 # 这个值是原查找表的最后那个元素的值 14 # 添加的个数由F[k]-1-high决定 15 k = 0 16 while high > F[k]-1: 17 k += 1 18 print(k) 19 i = high 20 while F[k]-1 > i: 21 lis.append(lis[high]) 22 i += 1 23 print(lis) 24 25 # 算法主逻辑。time用于展示循环的次数。 26 time = 0 27 while low <= high: 28 time += 1 29 # 为了防止F列表下标溢出,设置if和else 30 if k < 2: 31 mid = low 32 else: 33 mid = low + F[k-1]-1 34 35 print("low=%s, mid=%s, high=%s" % (low, mid, high)) 36 if key < lis[mid]: 37 high = mid - 1 38 k -= 1 39 elif key > lis[mid]: 40 low = mid + 1 41 k -= 2 42 else: 43 if mid <= high: 44 # 打印查找的次数 45 print("times: %s" % time) 46 return mid 47 else: 48 print("times: %s" % time) 49 return high 50 print("times: %s" % time) 51 return False 52 53 if __name__ == '__main__': 54 LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444] 55 result = fibonacci_search(LIST, 444) 56 print(result)
算法分析:斐波那契查找的整体时间复杂度也为O(log(n))。但就平均性能,要优于二分查找。但是在最坏情况下,比如这里如果key为1,则始终处于左侧半区查找,此时其效率要低于二分查找。
总结:二分查找的mid运算是加法与除法,插值查找则是复杂的四则运算,而斐波那契查找只是最简单的加减运算。在海量数据的查找中,这种细微的差别可能会影响最终的查找效率。因此,三种有序表的查找方法本质上是分割点的选择不同,各有优劣,应根据实际情况进行选择。
排序算法
列表排序是编程中一个最基本的方法,应用场景非常广泛,比如各大音乐、阅读、电影、应用榜单等,虽然python为我们提供了许多排序的函数,但我们那排序来作为算法的练习再好不过。
首先介绍的是最简单的三种排序方式:1 冒泡排序 2 选择排序 3 插入排序
冒泡排序:列表中每相邻两个如果顺序不是我们预期的大小排列,则交换。时间复杂度O(n^2)
def bubble(list): high = len(list)-1 #指定一个最高位 while high>0: for i in range(0,high): if list[i]>list[i+1]: #如果比下一位大 list[i],list[i+1] = list[i+1],list[i] #交换位置 high -=1 #最高位减1 return list #返回列表 print(bubble(list))
优化一下:
list = [3,1,5,7,8,6,2,0,4,9] def bubble(list): high = len(list)-1 #定一个最高位 for j in range(high,0,-1): exchange = False #交换的标志,如果提前排好序可在完整遍历前结束 for i in range(0,j): if list[i]>list[i+1]: #如果比下一位大 list[i],list[i+1] = list[i+1],list[i] #交换位置 exchange = True #设置交换标志 if exchange == False: return list # return list #返回列表 print(bubble(list))
选择排序:一趟遍历选择最小的数放在第一位,再进行下一次遍历直到最后一个元素。复杂度依然为O(n^2)
list = [3, 1, 5, 7, 8, 6, 2, 0, 4, 9] def choice(list): for i in range(0,len(list)-1): min_loc = i for j in range(i+1,len(list)-1): if list[min_loc]>list[j]: #最小值遍历比较 min_loc = j list[i],list[min_loc] = list[min_loc],list[i] return list print(choice(list))
插入排序:将列表分为有序区和无序区,最开始的有序区只有一个元素,每次从无序区选择一个元素按大小插到有序区中
list = [3,1,5,7,8,6,2,0,4,9] def cut(list): for i in range(1,len(list)-1): temp = list[i] for j in range(i-1,-1,-1): #从有序区最大值开始遍历 if list[j]>temp: #如果待插入值小于有序区的值 list[j+1] = list[j] #向后挪一位 list[j] = temp #将temp放进去 return list print(cut(list))
这三种排序方式时间复杂度都是O(n^2),不太高效,所以下面介绍几种更高效的排序方式
1 快速排序:好写的排序里最快的,快的排序里最好写的。步骤为1 提取 2 左右分开 3 递归调用
list = [3,1,5,7,8,6,2,0,4,9] def partition(left=0,right=len(list)-1,list): temp = list[left] while left < right: while left<right and list[right]>temp: #当右边值较大时,值不动 right -=1 list[left]=list[right] #否则移动到左边 while left<right and list[left]<temp: left +=1 list[right]=list[left] list[left]=temp return left #返回leftright都可以,值是一样的 def quick_sort(left,right,list): while left<right: #迭代中断 mid = partition(left,right,list) #获取中间位置 quick_sort(left,mid-1,list) #小序列进一步迭代 quick_sort(mid+1,right,list) #大序列进一步迭代 return list #返回列表 print(quick_sort(left,right,list))

1 ''' 2 快速排序,取一个元素将它左边放比他小,右边比它大 3 递归 4 http://idea.ibdyr.com 5 6 ''' 7 import random 8 9 10 def partition(li, left, right): 11 ###########解决办法########### 12 si = random.randint(left, right) 13 li[left], li[si] = li[si], li[left] #随机交换最左位置的元素,以免出现极端情况 14 ############################ 15 tmp = li[left] #记录下最左位置的元素 16 while left < right: #必须左边有元素才成立 17 while li[right] >= tmp and left < right: 18 # 从右边寻找一个小于tmp的值 19 right -= 1 20 li[left] = li[right]#将右边那个值赋予左边这个位置上 21 while li[left] <= tmp and left < right: 22 left += 1#从左边找一个大于tmp的值 23 li[right] = li[left]#将左边那个值放在右边的位置上 24 li[left] = tmp#将最开始左边位置的值放在左边位置上 25 return left 26 27 28 def quick_sort(li, left, right): 29 if left < right: # z至少两个元素 30 mid = partition(li, left, right) 31 quick_sort(li, left, mid - 1) 32 quick_sort(li, mid + 1, right) 33 34 35 li = list(range(10)) 36 random.shuffle(li) 37 quick_sort(li,0,len(li)-1) 38 39 ''' 40 # 快拍是最快的时间复杂度大概是O(nlogn) 41 问题: 42 递归效率低,递归深度问题 43 最坏情况 44 9 8 7 6 5 4 3 2 1 45 每层递归都只有一遍有数据 46 时间复杂度是n**2 47 这种情况在根本上无法避免 48 解决方法:随机找一个元素将它与第一个元素进行交换,无法完全避免 49 '''
快排的时间复杂度最佳情况是O(nlogn),最差情况是O(n^2)
下面要介绍堆排序了。在介绍堆排序之前先简单提一下树的概念:
树是一种数据结构(比如目录),树是一种可以递归的数据结构,相关的概念有根节点、叶子节点,树的深度(高度),树的度(最多的节点),孩子节点/父节点,子树等。
在树中最特殊的就是二叉树(度不超过2的树),二叉树又分为满二叉树和完全二叉树,见下图:

二叉树的储存方式有:1 链式储存 2 顺序储存(列表)
父节点和左孩子节点的编号下表的关系为 i --> 2i+1,右孩子则是i --> 2i+2 最后一个父节点为(len(list)//2-1) 由此可以通过父亲找到孩子或相反。
知道了树就可以说说堆了,堆分为大根堆和小根堆,分别的定义为:一棵完全二叉树,满足任一节点都比其孩子节点大或者小。
堆排序的过程:
- 建立堆
- 得到堆顶元素,为最值
- 去掉堆顶,将最后一个元素放到堆顶,进行再一次堆排序(迭代)
- 第二次的堆顶为第二最值
- 重复3,4直到堆为空
代码为:
list = [3, 1, 5, 7, 8, 6, 2, 0, 4, 9] def sift(low, high, list):#low为父节点,high为最后的节点编号 i = low j = 2 * i + 1 #子节点位置 temp = list[i] #存放临时变量 while j <= high: #遍历子节点到最后一个 if j < high and list[j] < list[j + 1]:#如果第二子节点大于第一子节点 j += 1 if temp < list[j]: #如果父节点小于子节点的值 list[i] = list[j] #父子交换位置 i = j #进行下一次编号 j = 2 * i + 1 else: break #遍历完毕退出 list[i] = temp #归还临时变量 def heap_sort(list): n = len(list) for i in range(n // 2 - 1, -1, -1): #从最后一个父节点开始 sift(i, n-1, list)#完成堆排序 for i in range(n - 1, -1, -1):#开始排出数据 list[0], list[i] = list[i], list[0]#首尾交换 sift(0, i - 1, list) #进行新一轮堆排序 return list print(heap_sort(list))
归并排序:假设列表中可以被分成两个有序的子列表,如何将这两个子列表合成为一个有序的列表成为归并。
原理如下图:
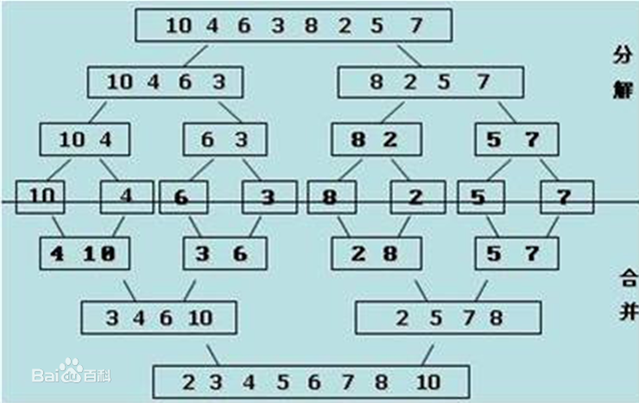
代码如下:
def merg(low,high,mid,list): i = low j = mid +1 list_temp = [] #定义临时列表 while i <=mid and j <=high: if list[i]<=list[j]: #分别比较有序子列表元素的大小 list_temp.append(list[i]) #添加进临时列表中 i +=1 else: list_temp.append(list[j]) j +=1 while i <= mid: list_temp.append(list[i]) i +=1 while j <= high: list_temp.append(list[j]) j +=1 list[low:high+1]=list_temp #将已完成排序的列表赋值给原列表相应位置 def merge_sort(low,high,list): if low < high: mid = (low+high)//2 #二分法 merge_sort(low,mid,list) merge_sort(mid+1,high,list)#递归调用, merg(low,high,mid,list) return list list = [3,1,5,7,8,6,2,0,4,9] print(merge_sort(0,len(list)-1,list))
version2 代码量更少:
def MergeSort(lists): if len(lists) <= 1: return lists num = int(len(lists) / 2) left = MergeSort(lists[:num]) right = MergeSort(lists[num:]) return Merge(left, right) def Merge(left, right): r, l = 0, 0 result = [] while l < len(left) and r < len(right): if left[l] < right[r]: result.append(left[l]) l += 1 else: result.append(right[r]) r += 1 result += right[r:] result += left[l:] return result print(MergeSort(list))
快排,堆排,归并的总结:
- 时间复杂度都是O(nlogn)
- 快排<归并<堆排(一般情况)
- 快排的缺点:极端情况效率较低,可到O(n^2),归并则是需要额外的开销,堆排则在排序算法中相对较慢