计算机组成与体系结构-浮点数表示

定点数:

是一种在计算机中表示和处理实数的方法，其中，小数点的位置是固定的，不会随着数值的大小而变化。

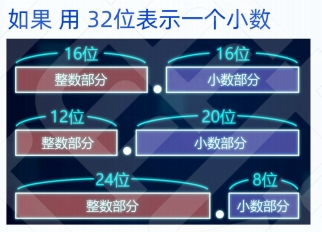
浮点数:

是计算机中用于表示实数的一种数据类型。小数点 位置浮动

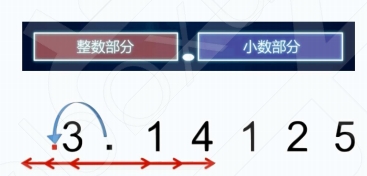
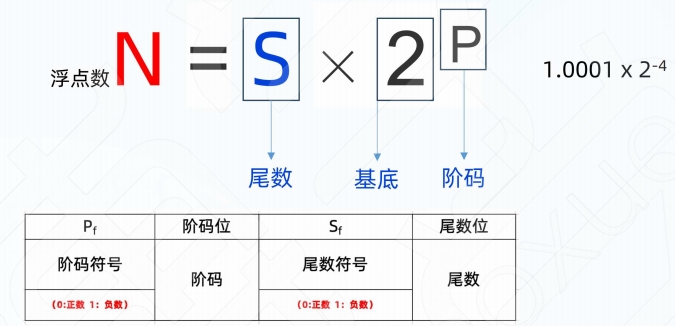
浮点数表示

浮点加减运算操作流程

首先，我们需要检查操作数，特别是是否存在零操作数。如果有一个或两个操作数为零，那么结果直接为零，无需进行后续计算。
接着，进行对阶操作。由于浮点数表示的精度有限两个不同大小的数相加或相减可能会导致溢出或下溢。对阶操作确保两个操作数的指数尽可能接近，以避免这些问题的发生。对阶的过程涉及调整阶码和尾数(有效数字或尾数部分)具体来说，当两个浮点数的阶码不相等时，需要将阶码较小的浮点数(即小阶)的尾数部分向右移动(相当于乘以2的负幕)，直到它的阶码与另一个浮点数的阶码相等。这是因为阶码较小的浮点数在数值上表示的是一个更小的数，因此它的尾数部分需要向右移动以增大其值，使其与另一个浮点数对齐，
然后，执行尾数的加法或减法运算。这一步是实际的数学运算，根据两个操作数的尾数执行加法或减法，
最后，进行规格化和舍入处理。这一步确保结果符合浮点数的表示规则:如果结果的小数部分为零，只保留指数部分;
如果结果超出了浮点数的表示范围，需要进行适当的舍入或截断操作。
所以，正确的浮点加(减)法操作流程是:零操作数检查 ->对阶操作 ->尾数加(减)运算 -规格化及舍入处理。

阶码(指数部分):

决定了浮点数可以表示的范围。阶码越长，可以表示的指数范围就越大

尾数(有效数字或分数部分):

决定了浮点数的精度。尾数越长，可以表示的有效数字位数就越多，精度也就越高

规格化:

阶码和尾数都是使用二进制表示

原码和补码

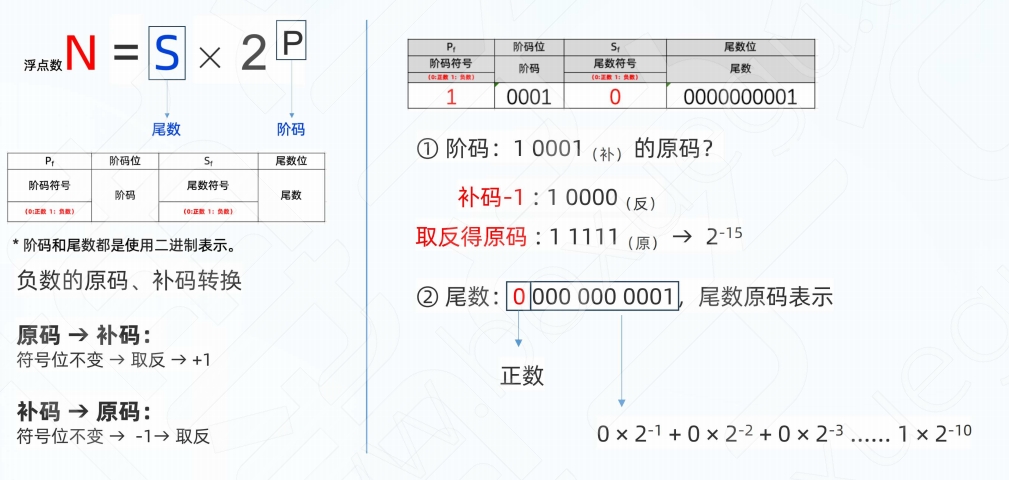
负数
原码符号位为 1
反码符号位不变，其他位按位取反
补码反码+1