Prufer 序列
Prufer 序列简介:
一个 Prufer 序列一一对应一个无根数,即:一个 Prufer 序列可以用于描述一颗无根树。
生成 Prufer 序列:
假定给出一颗 n 个节点的无根树,生成 Prufer 序列步骤如下:
- 寻找度为 1 且编号最小的节点,将其父节点加入 Prufer 序列,并在树中删除此节点;重复此步直到仅剩下两个节点。
- 最终生成的 Prufer 序列长度为 (n-2)。
下图中的树对应的 Prufer 序列为:3, 5, 1, 3
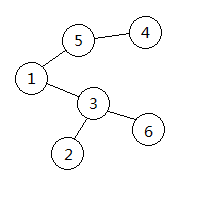
Prufer 序列生成树:
根据上述生成 Prufer 序列方法逆推即可。
Prufer 序列性质:
- 一个 Prufer 序列中节点出现的次数恰好为对应树中节点度数 -1 ;
- 对于一颗 n 节点的树,其 Prufer 序列长度恰好为 (n-2),且序列中的元素均为节点编号,据此可推出 n 个节点可生成 n^(n-2) 颗不同的树;
- 继续推广可得:n个节点的度依次为D1, D2, …, Dn的无根树共有 (n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ] 个;


