第六章实验报告(函数与宏定义)
实验项目:函数和宏定义实验
姓名:谢丽萍 试验地点:教学楼514教室 实验地点:2019 年4月30日
一、实验目的与要求
1、掌握函数的定义方法和调用规则
2、掌握在c语言程序中主调函数和背调函数之间进行数据传递的规则
3、了解函数的返回值及其类型,并用正确使用它
4、了解局部变量和全局变量的作用域及他们与存储分类的关系,理解变量的存在性和可见性的概念
5、练习递归函数的使用
6、理解宏的概念,掌握定义无参宏和代参宏的方法了解文件包含的概念,掌握其方法
7、理解内部函数和外部函数,了解外部函数的编译和链接的方法
二、实验内容
1、实验练习:函数的定义和调用
问题描述:编写程序,从键盘输入三角形的3条边,调用三角形面积函数求出其面积,名输出其结果。
流程图: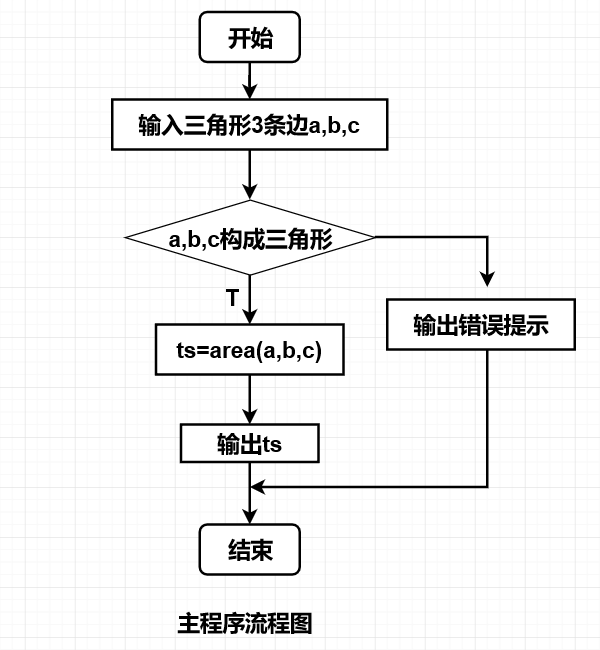
实验代码:
#include<stdio.h> #include<math.h> float area(float a,float b,float c) { float s,p,area; s=(a+b+c)/2; p=s*(s-a)*(s-b)*(s-c); area=sqrt(p); return (area); } main() { float x,y,z,ts; printf("please input the value of x and y and z:\n"); scanf("%f%f%f",&x,&y,&z); ts=area(x,y,z); if(x+y>=z&&x+z>=y&&y+z>=x) printf("area=%f\n",ts); else printf("data error!"); }
运行结果: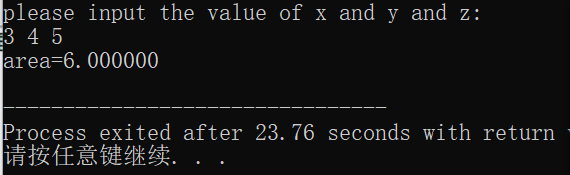
问题分析:这道题的思路还挺清晰的,难度不是很大,加上流程图的帮助,就没遇到什么问题。
2、实验练习:
问题描述:编写函数,求出从主调函数传来的数值i的阶乘值,然后将其传回主调函数并输出。
流程图: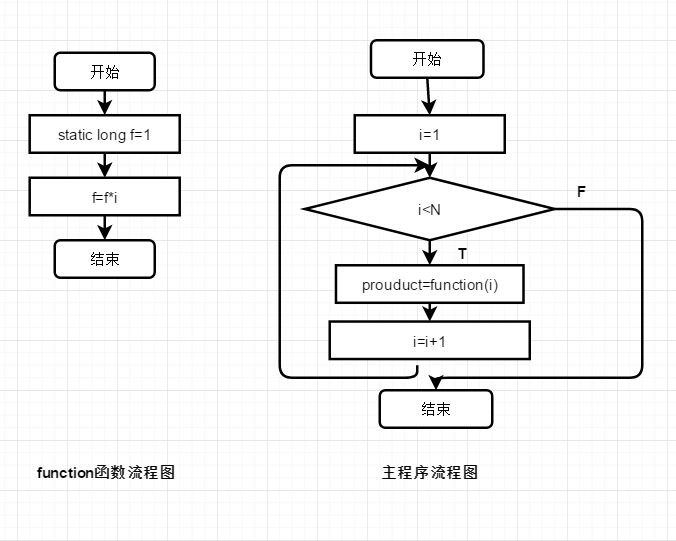
实验代码:
#include<stdio.h> int N=5; long function(int i) { static long f=1; f=f*i; return f; } main() { long product; int i; for(i=1;i<=N;i++) { product=function(i); printf("%d!=%ld\n",i,product); } }
运行结果: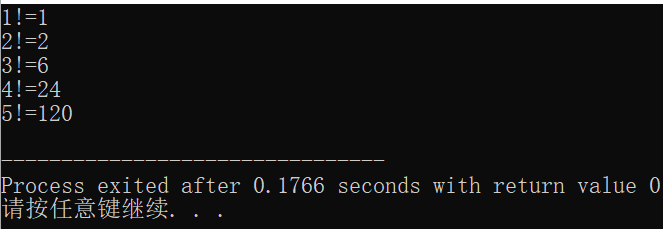
问题分析:这道题与上次讲的一道书上的例题相似,只是用的方法不同,这次是调用函数的调用来实现的,所以对比之前的方法,感觉这种方法更简单,代码更简洁,也更好理解。
3、实验练习:
问题描述编写程序,从键盘输入两个整数,调用gcd()函数求它们的最大公约数,并输出结果。
流程图: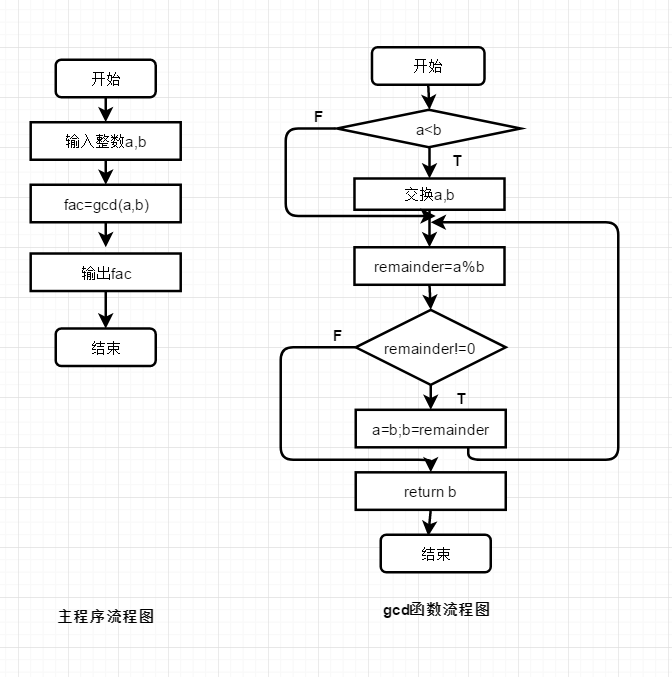
实验代码:
#include<stdio.h> int gcd(int a,int b) { int temp; int remainder; if(a<b) { temp=a; a=b; b=remainder; } remainder=a%b; while(remainder!=0) { gcd(a,b); } return b; } main() { int x,y; int fac; printf("please input two integers:\n"); scanf("%d%d",&x,&y); fac=gcd(x,y); printf("Thr great common divisor is:%d",fac); }
运行结果:
问题分析:这道题我不知道为什么回来后在自己的电脑上运行结果与在实验室的不同,这道题刚开始的时候有点卡住了,后来老师见同学上去讲了之后加上老师的分析,就理解了。但对于现在遇到的问题我很不解。
4、实验练习:
问题描述:输入整数n,输出高度为n的等边三角形。当n=5时的等边三角形。
流程图: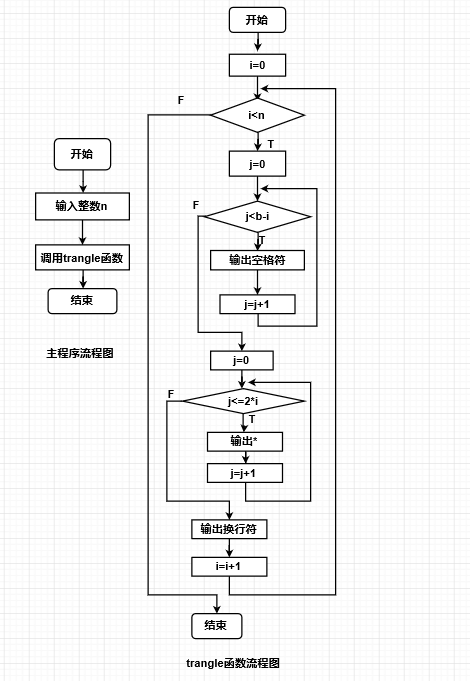
实验代码:
#include<stdio.h> trangle(int n) { int i,j; for(i=0;i<n;i++) { for(j=0;j<n-i;j++) printf(" "); for(j=0;j<=2*i;j++) printf("*"); putchar('\n'); } } main() { int n; printf("please input the value n:\n"); scanf("%d",&n); printf("\n"); trangle(n); }
运行结果:
问题分析:这道题之前有做过,所以做起来比较轻松。
5、实验练习:
问题描述:若正整数A的所有因子之和为B,而B的因子之和为A,则称A和B为一对亲密数。例如,6的因子之和为1+2+3=6,因此6与6为一对亲密数;又如,220的因子之和为1+2+4+5+10+11+20+22+44+55+110=284,而284的因子之和为1+2+4+71+142=220,因此220与284为一对亲密数。求500以内的所有亲密数对。
流程图: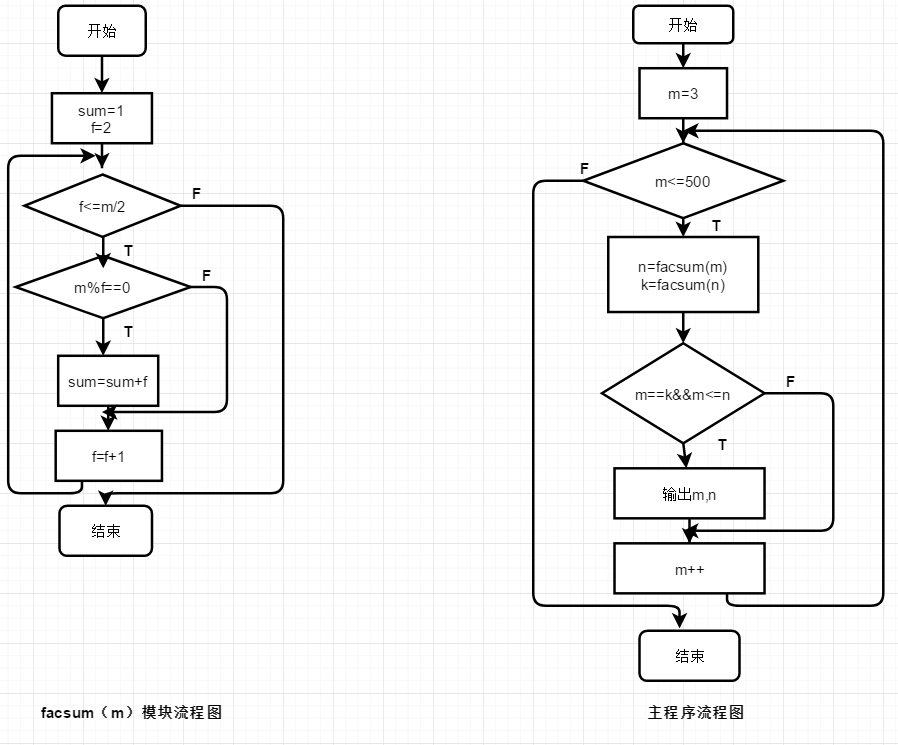
实验代码:
#include<stdio.h> int facsum(int m) { int sum=1,f=2; while(f<=m/2) { if(m%f==0) sum=sum+f; f++; } return sum; } main() { int m=3,n,k; while(m<=500) { n=facsum(m); k=facsum(n); if(m==k&&m<=n) printf("%d,%d\n",m,n); m++; } }
运行结果: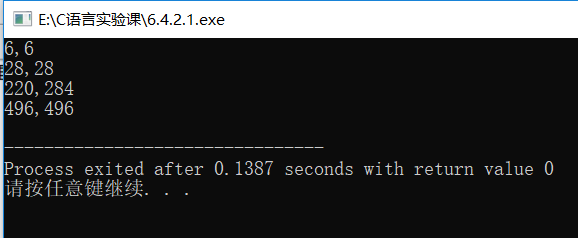
问题分析:这道题比较新颖,因为之前没接触过,再做的过程中虽说没遇上很大的困难,因为有流程图,但对于这道题还是值得去深刻的理解的。
三、实验小结
对于这次实验我还是觉得要多练习多想吧,因为只有不断的去想问题才有可能使自己的思路更开阔。不管怎样还是要多看书,要善于类比学习,这样才能更好的理解其中的精髓。



