二叉搜索树的前驱节点和后继节点

前驱结点：节点val值小于该节点val值并且值最大的节点 

后继节点：节点val值大于该节点val值并且值最小的节点

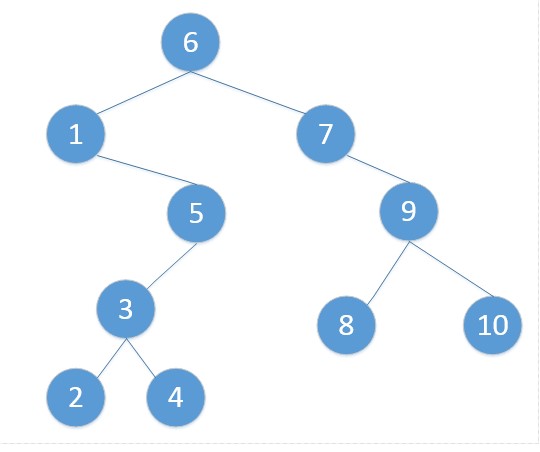
 二叉树的节点val值是按照二叉树中序遍历顺序连续设定。

前驱结点

• 如图4的前驱结点是3
• 2的前驱结点是1
• 6的前驱结点是5

后继节点

• 7的后继结点是8
• 5的后继节点是6
• 2的后继节点是3

前驱节点

1. 若一个节点有左子树，那么该节点的前驱节点是其左子树中val值最大的节点（也就是左子树中所谓的rightMostNode）
2. 若一个节点没有左子树，那么判断该节点和其父节点的关系 
   2.1 若该节点是其父节点的右边孩子，那么该节点的前驱结点即为其父节点。 
   2.2 若该节点是其父节点的左边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的右边孩子（可参考例子2的前驱结点是1），那么Q就是该节点的后继节点
   
   
   

后继节点

1. 若一个节点有右子树，那么该节点的后继节点是其右子树中val值最小的节点（也就是右子树中所谓的leftMostNode）
2. 若一个节点没有右子树，那么判断该节点和其父节点的关系 
   2.1 若该节点是其父节点的左边孩子，那么该节点的后继结点即为其父节点 
   2.2 若该节点是其父节点的右边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的左边孩子（可参考例子2的前驱结点是1），那么Q就是该节点的后继节点

实现

/**
* 前驱元素
* **/
public BSTreeNode<T> Pred(BSTreeNode<T> node) {
	if (node.left != null) {
		return Max(node.left);
	}
	BSTreeNode<T> parent = node.parent;
	while (parent != null && node != parent.right) {
		node = parent;
		parent = node.parent;
	}
	return parent;
}

/**
* 后继元素
* **/
public BSTreeNode<T> Succ(BSTreeNode<T> node) {
	if (node.right != null) {
		return Min(node.right);
	}
	BSTreeNode<T> parent = node.parent;
	while (parent != null && node != parent.left) {
		node = parent;
		parent = node.parent;
	}
	return parent;
}

null