立体视觉图像校正
最近在学习李博的一系列博客，在这里想做个记录（对原文简洁化了一下并加了代码实现），如果有朋友想看原文的话末尾有链接
研究对极约束的目的
对两幅图像的二维匹配搜索变成一维，节省计算量，排除虚假匹配点，让匹配的搜索空间变小，略去完全不可能是解的像素。
对极约束，是将搜索空间约束到像平面内的一条直线上。
极平面和极线
图1 对极约束
两个相机的光心O1, O2(对应上图中的C1和C2)和空间点P形成一个三角关系，它们确定了一个空间平面，这个平面和两个像平面都相交，交线分别是l1, l2，在l1上的所有点，其匹配点一定在l2上，这就是对极约束，它将匹配的搜索空间限制到了一条直线上，大大减少了搜索的空间大小，提高匹配效率。而两条直线l1, l2就叫做极线，称它们为极线对。
极线校正
极线校正是通过两个相机进行旋转，并重新定义新的平面，让极线对共线且平行于像平面的某条坐标轴（通常是水平轴），该操作同时建立了新的立体像对。纠正完成后，同一匹配点对，位于两个视图的同一行内，这意味着它们只有水平坐标（列坐标）的差异，这个差异称为视差（d）,数学定义上，视差d = col(p1) - col(p2)(col指水平方向坐标，或者说列坐标)
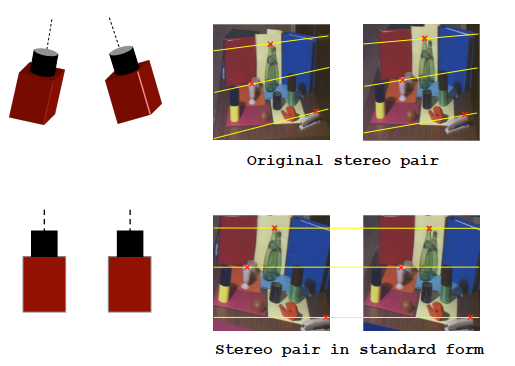
图2 极线校正
极线校正的方法
（1）Fusiello校正法
目标：
1.极线对平行于某条坐标轴。
2.极线对共线，匹配点对位于像平面的同一行。
为达到这两个目标，极线校正需要通过旋转相机和重新定义像平面来做，实际上，两个操作的本质在于重新定义投影矩阵M= K[R| - RC]。通过旋转相机重定义旋转矩阵R -> Rn让新的像平面共面且平行于相机基线，则可以满足目标1，而重定义像平面的内参K -> Kn使双相机有同样的内参数，可以满足目标2。
如下图所示，纠正后的像平面，水平u轴和基线C1C2平行，焦距f和主点坐标相等。
图3 Fusiello校正法
具体地，第一步是旋转相机让像平面共面且平行于相机基线，实际上是重新定义一个相机坐标系，首先新相机坐标系设计如下：
1.首先是X轴，显然要和相机基线平行，才能让像平面平行于相机基线，所以X轴基向量为rx = (C1-C2) / || C2 - C1||。
2.其次是Y轴，它是和X轴正交的，可以设置一个任意的向量k, 让Y轴和X轴以及向量k正交，所以Y轴的基向量为ry = K X rx。关于这个k，理论上任意都可以，但是我们希望新坐标系下的图像和原图的范围尽量一致，所以尽量选择和旧的Y轴近似的朝向，在Fusiello法中，k为旧的Z轴所表示的单位向量。
3.最后是Z轴，X和Y轴确定后，Z轴的基向量就可以通过两者的叉乘基于右手法则得到：rz = rx X ry
确定了新坐标的3个基向量，就可以确定新的旋转矩阵
第二步，是重新设计新的内参矩阵Kn，理论上，K是可以任意设置的，但是为了和旧相机尽量保持一致，Fusiello法选择的是Kn = (Kleft + Kright) / 2。且把倾斜因子设置为0。
确定K和R后，我们得到新的投影矩阵Mn = Kn[Rn| - RnC]。
接下来就是校正过程，具体的过程是对于新图像像素pn，通过变换矩阵T计算旧图像上的像素p：p = T pn，再通过双线性内插获取像素值赋给新图像。所以关键就在于如何得到变换矩阵T。
目前来说，我们旋转了相机以及重定义内参，这样变换了旋转矩阵R -> Rn和内参矩阵K -> Kn，而没有改变的是相机中心C。所以现在有新旧两组投影矩阵
其中， Q = K R，Qn = Kn Rn。
经过推导可得：
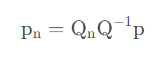
这就是新旧图像的转换公式，而Ｔ＝Qn Q-1即是转换矩阵。
对于两个相机，根据公式可以计算各自的转换矩阵T1，T2。
（2） Bouguet校正法
将左右相机之间的旋转矩阵R拆分，从而两相机平面处于同一平面上，此时并没有行对齐。
然后求解对齐校正矩阵。定义左右相机光心之间的单位平移向量e1为
定义与e1正交的向量为e2，归一化后表示为
将单位向量e1和e2作叉积，得到向量e3，表示为
因此，得到行对齐矩阵Rrect，表示为
综合左右相机旋转矩阵和行对齐校正矩阵，得到左右相机的立体校正矩阵为
根据立体校正矩阵变换左右相机图像，使得左右相机图像共面且完全行对齐，完成立体校正。
Bouguet校正实现代码
#include <iostream> #include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/imgproc/imgproc.hpp> #include <opencv2/calib3d.hpp> // #include "Matrix.h" using namespace cv; using namespace std; //cv::Mat imageSize(1024, 1280, CV_8UC3, cv::Scalar(100)); cv::Size imagesize(1024, 1280); cv::Mat cameraMatrix1; //左相机矩阵 cv::Mat distCoeffs1; //左相机畸变系数矩阵 cv::Mat cameraMatrix2; //右相机内参矩阵 cv::Mat distCoeffs2;//右相机畸变系数矩阵 cv::Mat R, T, E, F; //R 旋转矢量 T平移矢量 E本征矩阵 F基础矩阵 cv::Mat R1, R2, P1, P2, Q; //校正旋转矩阵R，投影矩阵P 重投影矩阵Q cv::Mat mapx1, mapy1, mapx2, mapy2; //映射表 Rect validROI1, validROI2; //图像校正之后，会对图像进行裁剪，这里的validROI就是指裁剪之后的区域 bool isopen = true;//用于判断相机获取图像对时是否打开 cv::Mat imgLeft;//校正后的左图像 cv::Mat imgRight;//校正后的右图像 cv::Mat disparity8U;//将视差值范围投影到0-255的视差图 cv::Mat disparity_real;//真实视差值的视差图 cv::Mat disparity;//调用函数得到的原始视差图 int numDisparities = 7;//匹配搜索的视差范围，规定必须能被16整除 int blockSize = 7;//匹配窗口大小 int UniquenessRatio = 5; cv::Mat _3dImage;//三维坐标图 bool readFile(string filename) { FileStorage fs(filename, FileStorage::READ); if (fs.isOpened()) { fs["cameraMatrix1"] >> cameraMatrix1; fs["distCoeffs1"] >> distCoeffs1; fs["cameraMatrix2"] >> cameraMatrix2; fs["distCoeffs2"] >> distCoeffs2; fs["R"] >> R; fs["T"] >> T; fs.release(); /* cout<<"Succeed to read the Calibration result!!!"<<endl; cout<<"左相机内参矩阵："<<endl<<cameraMatrix1<<endl; cout<<"右相机内参矩阵："<<endl<<cameraMatrix2<<endl; cout<<"distCoeffs1:"<<endl<< distCoeffs1 <<endl; cout<<"distCoeffs2:"<<endl<< distCoeffs2 <<endl; cout<<"R:"<<endl<<R<<endl; cout<<"T:"<<endl<<T<<endl;*/ return true; } else { cerr << "Error: can not open the Calibration result file!!!!!" << endl; return false; } } int main(int argc, char** argv) { if (argc < 3) { std::cout << "参数过少，请至少指定左右影像路径！" << std::endl; return -1; } //···············································································// // 读取影像 std::string path_left = argv[1]; std::string path_right = argv[2]; cv::Mat img_left_c = cv::imread(path_left, cv::IMREAD_COLOR); cv::Mat img_left = cv::imread(path_left, cv::IMREAD_GRAYSCALE); cv::Mat img_right = cv::imread(path_right, cv::IMREAD_GRAYSCALE); if (img_left.data == nullptr || img_right.data == nullptr) { std::cout << "读取影像失败！" << std::endl; return -1; } if (img_left.rows != img_right.rows || img_left.cols != img_right.cols) { std::cout << "左右影像尺寸不一致！" << std::endl; return -1; } //************从标定文件中读取标定结果 const string filename = "D:\\Postgraduate\\VS_Vision_Code\\stereoRectify\\cameraParameter.yaml"; bool readOK = readFile(filename); if (!readOK) { cerr << "failed to readfile!" << endl; return -1; } /**************************************************************************************/ /* 要实现立体校正，使左右图像共平面且行对准，需要用到以下参数： cameraMatrix1, distCoeffs1, R1, P1 cameraMatrix2, distCoeffs2, R2, P2 其中内参矩阵和畸变系数通过标定程序获得，但R1、P1、R2、P2的值，opencv提供了两种方法： 1. Hartley方法； 这种方法称为“非标定立体校正方法”，也就是说不用通过标定获得的内参矩阵和畸变系数获取 R1、P1、R2、P2的值，直接根据匹配点计算基础矩阵F，再进一步计算R1、P1、R2、P2。 这种方法主要用到两个函数：findFundamentalMat()和stereoRectifyUncalibrated() 具体的原理说明参考《Learning opencv》中文版498页。 2. Bouguet方法 这种方法称为“标定立体校正方法”，它是根据立体标定获得的内参矩阵、畸变系数、R和T作为 输入，利用stereoRectify()函数得到R1、P1、R2、P2的值。 两种方法的选用根据bool类型的useCalibrated变量决定， 当useCalibrated=true时，调用Bouguet方法； 当useCalibrated=false时，调用Hartley方法； */ /**************************************************************************************/ cv::stereoRectify(cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imagesize, R, T, R1, R2, P1, P2, Q, CALIB_ZERO_DISPARITY, -1, imagesize, &validROI1, &validROI2); /* cout << "重投影矩阵Q:" << endl << Q << endl; cout << "打印左摄像机投影矩阵P1:" << endl << P1 << endl; cout << "打印右摄像机投影矩阵P2:" << endl << P2 << endl; cout << "打印新的左摄像机旋转矩阵R1：" << endl << R1 << endl; cout << "打印新的右摄像机旋转矩阵R2：" << endl << R2 << endl;*/ /*根据stereoRectify计算出来的R和P来计算图像的映射表mapx, mapy mapx, mapy这两个映射表接下来可以给remap()函数调用，来校正图像，使得两幅图像共面并且行对准 initUndistortRectifyMap()的参数newCameraMatrix就是校正后的摄像机矩阵。 在openCV里面，校正后的计算机矩阵Mrect是跟投影矩阵P一起返回的。 所以我们在这里传入投影矩阵P，此函数可以从投影矩阵P中读出校正后的摄像机矩阵 */ cv::initUndistortRectifyMap(cameraMatrix1, distCoeffs1, R, P1, imagesize, CV_32FC1, mapx1, mapy1); cv::initUndistortRectifyMap(cameraMatrix2, distCoeffs2, R, P2, imagesize, CV_32FC1, mapx2, mapy2); //校正 cv::remap(img_left, imgLeft, mapx1, mapy1, INTER_LINEAR); cv::remap(img_right, imgRight, mapx2, mapy2, INTER_LINEAR); /***************把左右图像的校正结果显示到同一画面上进行对比*********************/ cv::Mat canvas; double sf = 0.7; int w, h; w = cvRound(imagesize.width * sf); h = cvRound(imagesize.height * sf); canvas.create(h, w * 2, CV_8UC1); //左图像画到画布上 //得到画布的左半部分 Mat canvasPart = canvas(Rect(w * 0, 0, w, h)); //把图像缩放到跟canvasPart一样大小并映射到画布canvas的ROI区域中 resize(imgLeft, canvasPart, canvasPart.size(), 0, 0, INTER_AREA); //右图像画到画布上 canvasPart = canvas(Rect(w, 0, w, h)); resize(imgRight, canvasPart, canvasPart.size(), 0, 0, INTER_AREA); //画上对应的线条 for (int i = 0; i < canvas.rows; i += 32) line(canvas, Point(0, i), Point(canvas.cols, i), Scalar(255, 255, 255), 1, 8); imshow("rectified", canvas); cv::waitKey(0); /*cv::imshow("原左图", img_left); cv::waitKey(0);*/ return 0; }
参考博客：https://blog.csdn.net/rs_lys/article/details/119837782
