坐标系和相机参数

针孔模型

                

       立体视觉的三个关键坐标系是影像坐标系、相机坐标系、世界坐标系。

影像坐标系

       影像坐标系是一个二维坐标系，是在影像内建立的坐标系，描述像素点在影像中的位置，分为以像素为单位的(u, v)坐标系以及以物理尺寸为单位的(x, y)坐标系。(这里讲的和图的对应关系不太理解，先搁置)。在计算机视觉中，(u, v)坐标系以左上角位置为原点，u轴和v轴分别平行于图像平面的两条垂直边（u轴朝右，v轴朝下），如图3左所示；（x, y）坐标系以像主点(u0，v0)为原点，x轴和y轴分别与u轴和v轴平行且方向一致，如图3右所示。

                                       

                                                                                                  图3 影像坐标系

       像主点：摄影中心到成像平面的垂点。

       已知像素到物理尺寸的转换关系，即一个像素的物理尺寸，也就是像元尺寸dx*dy，就可以在两类坐标系之间相互转换：

                                                                

为了便于矩阵运算，写成矩阵形式：

                                                    （2）

相机坐标系

       相机坐标系是一个三维空间坐标系，是非常关键的一个坐标系，建立了影像坐标系和世界坐标系之间的联系。所以建立相机坐标系时，有一个很关键的考量是如何能更好的把影像坐标系和世界坐标系之间联系起来。

       两个三维坐标系（相机和世界）之间的转换用旋转和平移就可以方便表达，重点是三维的相机坐标系和二维的影像坐标系之间如何更好转换。

      方案：相机坐标系的原点在相机中心，XY轴和影像xy坐标系的xy轴平行，Z轴垂直于像平面且朝向像平面，Z轴和像平面的交点正是影像xy坐标系的原点（像主点）。如图4所示。                                                 

                                                                   图4 相机坐标系

       在此方案下，像平面上的所有像素点在相机坐标系下的Z坐标等于焦距f，XY坐标和影像xy坐标系下的值相等，即若像素点p在影像xy坐标系下的坐标为(x, y)，则其在相机坐标系下的坐标为(x, y, f)。

根据中心投影的特征，假设像素点p是空间点P的投影点，像素p对应的空间点在相机坐标系下的坐标为(Xc, Yc, Zc)。

                                               

                                                                                        图5 相机坐标系2

若两点位于从坐标系原点发出的同一条直线上，则该两点坐标成等比例关系，即

                                               

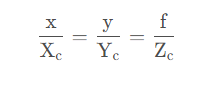
为便于矩阵运算，写成矩阵形式：

                                             （4）

结合式（2）和式（4），可以把相机坐标系转换成uv坐标系，即

                  

通常把Zc称作尺度因子，把中间的3X3矩阵叫做内参矩阵，简单的表达式如下：

                                            

 内参矩阵

       内参矩阵中的f/dx，f/dy实际是将以物理尺寸为单位的焦距f转换成像素为单位的焦距值，记fx = f/dx, fy = f/dy。最终得到内参表达：

                                                     

       由于制造工艺偏差，像素的纵向边界和y轴并不平行而是倾斜一定的角度，于是在K矩阵中引入一个倾斜因子s，此时K矩阵表示为：

                                                                  

 最后相机坐标到uv坐标的转换公式为：

                                                             

 世界坐标系

       世界坐标是一个固定的三维坐标系，它旨在将空间中的所有点都统一到同一个坐标系下表达，在不同的应用场景中，世界坐标系的定义并不一样，在相机标定中，将标定板的某个角点作为世界坐标系。

                                                                   

                                                                                  图6 世界坐标系

世界坐标系和相机坐标系都是三维坐标系，它们之间可以用旋转平移来做变换。

                                                      

                                                                                 图7 坐标系之间的旋转平移

        假设空间点P在世界坐标系中的坐标为(Xw, Yw, Zw)，则可以通过一个3X3的单位正交旋转矩阵R和3X1的平移矢量t来转换成相机坐标系(Xc, Yc, Zc):

                                                        

另一种形式：

                                                    

把旋转矩阵R和平移矢量t称为相机的外参矩阵

 外参矩阵

       外参矩阵描述的是世界坐标系到相机坐标系之间的转换关系。

世界坐标系到相机坐标系的简单表达式变换：

                                          

投影矩阵

       在实践过程中，最直接接触的是影像uv坐标系和世界坐标系，在影像三维重建中，通常前者是输入，后者是输出，所以将世界坐标系转换成uv坐标系是很关键的转换。

世界坐标系到uv坐标系的转换：

                        

       世界坐标系到影像坐标系的转换实际上表达的是透视投影中空间点到像点的投影关系，所以把该转换矩阵叫做投影矩阵M，通过矩阵运算可知投影矩阵是一个3X4的矩阵，它是内参矩阵和外参矩阵的乘积。

简单表达式变换：

                            

 

 

 

 

参考博客：https://ethanli.blog.csdn.net/article/details/113248118，李博

版权声明：本文为CSDN博主「李迎松~」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。