霍夫曼编码

　　最近还接触到了一些关于霍夫曼编码的题目，如下一题：

　　某段文本中各个字母出现的频率分别是{a:4，b:3，o:12，h:7，i:10}，使用哈夫曼编码，则哪种是可能的编码：（ ）

　　A  a(000)  b(001)  h(01)  i(10)  o(11)

　　B  a(0000)  b(0001)  h(001)  o(01)  i(1)

　　C  a(000)  b(001)  h(01)  i(10)  o(00)

　　D  a(0000)  b(0001)  h(001)  o(000)  i(1)

　　看完下文就知道上题的答案是什么了。

一个简明的例子

　　这个例子摘自酷壳的一篇博文Huffman 编码压缩算法。

　　如果我们需要来压缩下面的字符串： “beep boop beer!” 

　　首先，我们先计算出每个字符出现的次数，我们得到下面这样一张表 :

　　 

　　然后，我们把这些东西放到Priority Queue中（用出现的次数据当 priority），我们可以看到，Priority Queue 是以Prioirry排序一个数组，如果Priority一样，会使用出现的次序排序：下面是我们得到的Priority Queue：

　　

　　接下来就是我们的算法——把这个Priority Queue 转成二叉树。我们始终从queue的头取两个元素来构造一个二叉树（第一个元素是左结点，第二个是右结点），并把这两个元素的priority相加，并放回Priority中（再次注意，这里的Priority就是字符出现的次数），然后，我们得到下面的数据图表：

　　

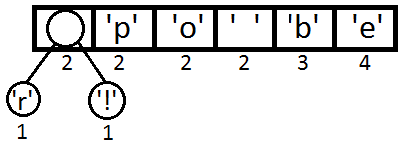
　　同样，我们再把前两个取出来，形成一个Priority为2+2=4的结点，然后再放回Priority Queue中 :

　　

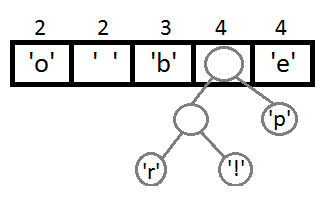
　　继续我们的算法（我们可以看到，这是一种自底向上的建树的过程）：

　　

　　

　　

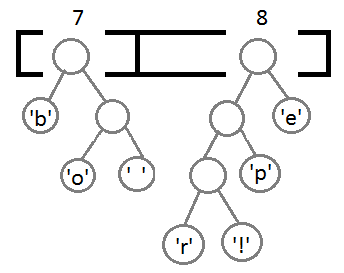
　　最终我们会得到下面这样一棵二叉树：

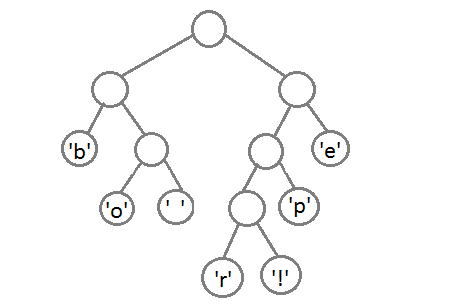
　　此时，我们把这个树的左支编码为0，右支编码为1，这样我们就可以遍历这棵树得到字符的编码，比如：‘b’的编码是 00，’p’的编码是101， ‘r’的编码是1000。我们可以看到出现频率越多的会越在上层，编码也越短，出现频率越少的就越在下层，编码也越长。

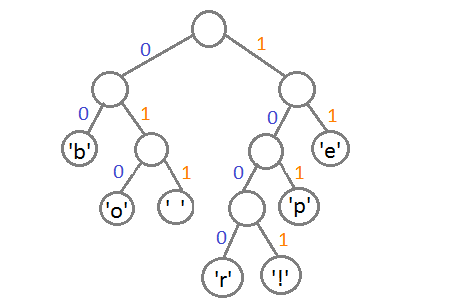
　　最终我们可以得到下面这张编码表：

　　

　　

　　看完这个例子，我们也就知道本文开头的题目的答案是A了。

简要证明

　　这里，我们只证明为什么出现频率低的节点要在霍夫曼树下层，而出现频率高的要在其上层呢？

　　参考博文知其所以然（三）：为什么算法这么难？：

　　假设这两个叶子节点的频率为f1和f2，深度为d1和d2，互换它们的时候，其他叶子节点的cost保持不变，令为常量C，那么互换前总cost为C+f1d1+f2d2，互换后为C+f1d2+f2d1，既然互换之后的树一定更”差“那么就是说f1d1+f2d2 < f1d2 + f2d1，简单变换一下就得到结论：f1(d1-d2)<f2(d1-d2)，也就是说如果d1<d2，那么f1必然>f2，如果d1>d2，那么f1必然<f2。换言之就是叶子节点的深度越高，频率必须越低，否则就不可能是最优霍夫曼树。那么，之前我们觉得不那么显然的结论便呼之欲出了：频率最低的叶子节点必然位于树的最底层，频率最高的叶子节点必然位于树的最高层。

　　注：cost of tree = Σ freq(i) * depth(i)