贝叶斯理解

【概率论与数理统计】全概率公式和贝叶斯公式

 

注：很久以前就知道这两个公式，但一直仅限于了解。直到最近学习edx上的课程，才对这两个公式有了新的理解，记录于此。

 

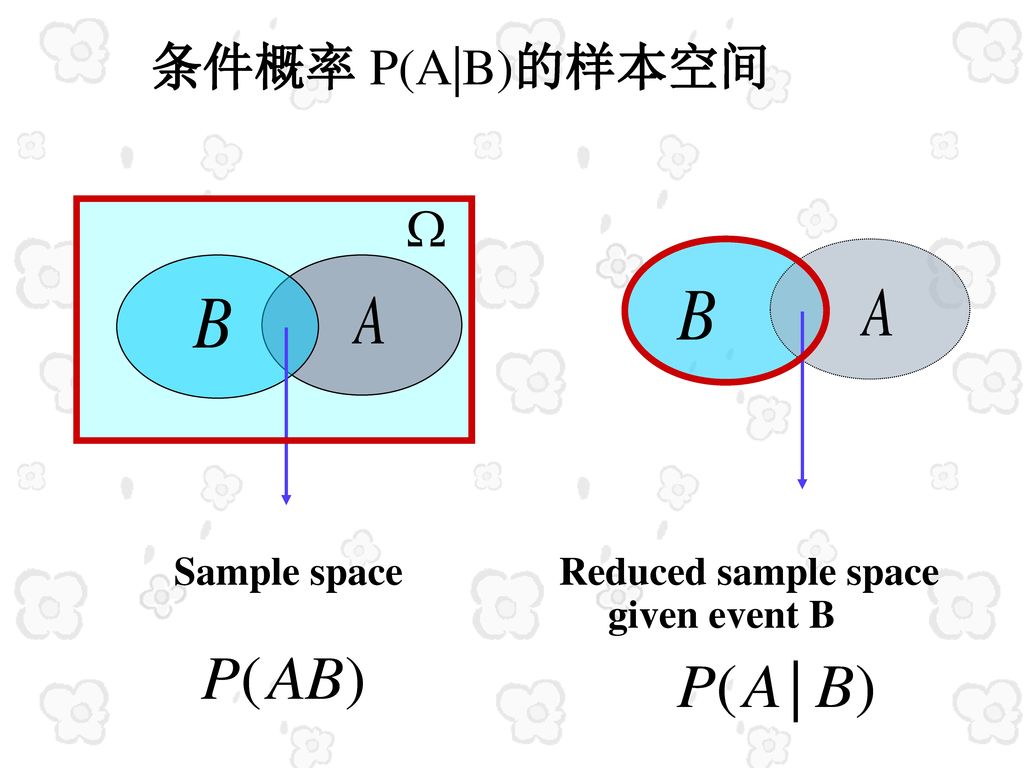
1. 条件概率公式

---

 设A, B是两个事件，且P(B)>0， 则在事件B发生的条件下，事件A发生的条件概率(conditional probability)为：

P(A|B)=P(AB)/P(B)

条件概率是理解全概率公式和贝叶斯公式的基础，可以这样来考虑，如果P(A|B)大于P(A)则表示B的发生使A发生的可能性增大了。

在条件概率中，最本质的变化是样本空间缩小了——由原来的整个样本空间缩小到了给定条件的样本空间。

 

2. 乘法公式

---

 2.1 乘法公式

由条件概率公式得：

 P(AB) = P(B)·P(A|B) = P(A)·P(B|A)

上面的式子就是乘法公式。

 

2.2 乘法公式的推广

对于任何正整数n≥2，当P(A₁A₂...A_n-1) > 0 时，有：

P(A₁A₂...A_n-1A_n) = P(A₁)P(A₂|A₁)P(A₃|A₁A₂)...P(A_n|A₁A₂...A_n-1)

 

3. 全概率公式

---

 3.1 前提假设

设B₁，B₂，....为有限或无限个事件，它们两两互斥且在每次试验中至少发生一个，即：

• 不重，B_i ∩ B_j = ∅（不可能事件）i≠j ,
• 不漏，B₁∪B₂∪.... = Ω（必然事件）.

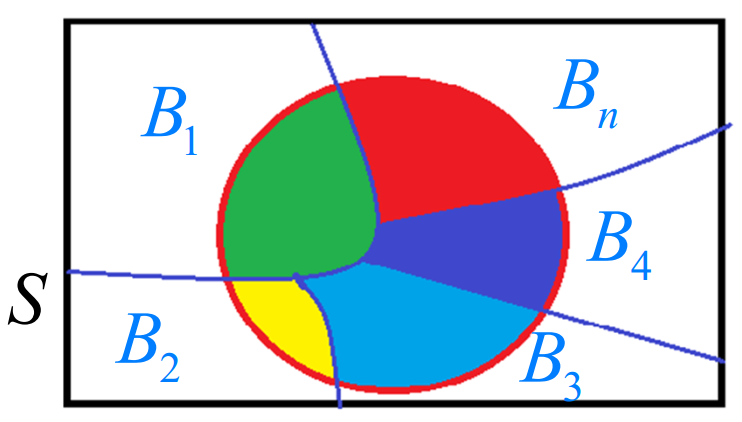  图1：B₁ - B_n是对S的一个划分

这时，称事件组 B₁, B₂,...是样本空间S的一个划分，把具有这些性质的一组事件称为一个“完备事件组”。

设 B₁, B₂,...是样本空间S的一个划分，A为任一事件（图1中红圈内部区域），则：

 

P(A)=∑i=1nP(Bi)P(A|Bi)(1)P(A)=∑i=1nP(Bi)P(A|Bi)(1)

 

 上式即为全概率公式（formula of total probability)

 也可以分为两步来看全概率公式：

 

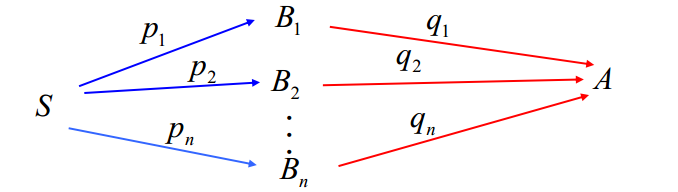
图2：分两步看全概率公式，S先被划分为n个子集B₁ - B_n，然后每个子集的发生会对A的发生产生不同程度的影响

 

设P(B_j) = p_j, P(A|B_j) = q_j, j = 1, 2, ..., n

则

P(A)=∑j=1npjqj(2)P(A)=∑j=1npjqj(2)

 

 

在运用全概率公式时的已知未知条件为：

• 划分后的每个小事件的概率，即P(B_i), i = 1, 2, ..., n；
• 每个小事件发生的条件下，A发生的概率，即P(A|B_i), i = 1, 2, ..., n；
• 求解目标是计算A发生的概率，即P(A)。

 

3.2 意义

全概率公式的意义在于，当直接计算P(A)较为困难，而P(B_i)，P(A|B_i)  (i=1,2,...)的计算较为简单时，可以利用全概率公式计算P(A)。思想就是，将事件A分解成若干个小事件，通过求每个小事件的概率，然后相加从而求得事件A的概率。

而将事件A进行分割的时候，不是直接对A进行分割，而是先找到样本空间S的一个划分B₁,B₂,...B_n,这样事件A就被事件AB₁,AB₂,...AB_n分解成了n部分，即A = AB₁ + AB₂ + ... + AB_n, 每一B_i发生都可能导致A发生相应的概率是P(A|B_i)，由加法公式得

    P(A) = P(AB₁) + P(AB₂) + .... + P(AB_n)

= P(B₁)P(A|B₁) + P(B₂)P(A|B₂) + ... +P(B_n) P(A|B_n)

 

4. 贝叶斯公式

---

与全概率公式解决的问题相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因（即大事件A已经发生的条件下，分割中的小事件B_i在A发生的条件下的概率），设B₁,B₂,...是样本空间S的一个划分，则对任一事件A（P(A)>0），有

 

P(Bi|A)=P(Bi)P(A|Bi)∑j=1nP(Bj)P(A|Bj)(3)P(Bi|A)=P(Bi)P(A|Bi)∑j=1nP(Bj)P(A|Bj)(3)

 

上式即为贝叶斯公式(Bayes formula)，B_i 常被视为导致试验结果A发生的“原因”，P(B_i)(i=1,2,...)表示各种原因发生的可能性大小，故称先验概率（权重）；P(B_i|A)(i=1,2...)则反映当试验产生了结果A之后，再对各种原因概率的新认识，故称后验概率。

如果参考图2，分成两步来看，B发生在A之前，且B有多种情况（B₁ - B_n）。在运用贝叶斯公式时，一般已知和未知条件为：

• B的多种情况中到底哪种情况发生了是未知的，但是每种情况发生的概率已知，即P(B_j)；
• 事件A是已经发生的确定事实，且每种B发生条件下A发生的概率已知，即P(A|B_j)；
• P(A)未知，需要使用全概率公式计算得到；
• 求解的目标是用B的某种情况B_i的无条件概率求其在A发生的条件下的有条件概率P(B_i|A)

 

5. 小结

---

如果我们把事件A看成“结果”，把诸事件B₁，B₂，…看成是导致这个结果的可能的“原因”，则可以形象地把全概率公式看做“由原因推结果”；而贝叶斯公式则恰好相反，其作用在于“由结果推原因”：现在有一个“结果”A已经发生了，在众多可能的“原因”中，到底是哪一个导致了这个结果？这是一个在日常生活和科学技术中常要问到的问题。贝叶斯公式说，各原因可能性的大小与P(B_i|A)成比例。

贝叶斯公式最神奇之处在于将条件概率中的因和果调换了位置，可以用下面的式子表示：

P(B|A) = P(因|果) = P(因)P(果|因)/P(果)

 

6. 例题

---

问题1：

设某公路经过的货车与客车的数量之比为1:2，货车中途停车修车的概率为0.02，客车为0.01，今有一辆汽车中途停车修理，则该车是货车的概率是多少？

解答：

 原本汽车中途停车维修的概率应该与车的数量成正比，即在只考虑车的数量时，停下来的车为货车的概率为P(A₁)，即1/3；

但是当我们进一步观察，加入更多的信息（每种类型的车的停车维修的概率）后，判断停下来的车为货车的概率增加到了1/2，也就是说B的发生使得A₁（观察到货车停下来维修）发生的概率变大了。（货车的数量虽然少，但是经过长期观察，货车出故障的概率是客车的2倍<获得了新的信息>，因此货车停在路边维修的概率就增加了）

 

问题2：

 装有10件某产品（乒乓球）（其中一等品5件，二等品3件，三等品2件）的箱子中丢失一件产品，但不知是几等品，今从箱中任取2件产品，结果都是一等品，则丢失的也是一等品的概率为？

 

解答：

由于我们不知道丢失了哪种球，最直接的猜测就是丢每种球的概率与球的数量成正比。即，丢的球是一等品的概率为1/2 = P(A₁)。

但是为了更加准确的推测到底丢了什么球，只能通过一些可行的方法，获得更多的信息。这里采用了"任取两个球出来"这种试验方法，然后根据试验结果得到了更加准确的结果3/8，也就是说，这一结果降低了我们前面直接根据球的数量预测出的概率。（因为任取两个都是一等品，说明剩下的球中，取到一等品的概率很大，因此丢的可能性就变小了）

 

问题3：

爱丽丝的口袋里有5枚硬币：两枚是正常的硬币（都有正反两面，normal），两枚硬币的两面都是正面（double-head），最后一枚硬币的两面都是背面（double-tail）。她随机取出一枚硬币，也没看是哪种硬币，然后投掷：

a). 硬币落地后，朝下的一面为正面的概率？

b). 硬币落地后，正面朝上，那么朝下的一面也是正面的概率？

c). 如果爱丽丝将b)中取到的硬币丢掉，重新从口袋中取出一枚硬币，还是没看是哪种硬币，然后投掷，则当硬币落地后正面朝上的概率？

 

解答：

首先，整个事情分成了两个大的步骤：

1. 第一步取出一个硬币（相当于图2中的B，有多种类型的硬币可以取）；
2. 抛出硬币，得到硬币落地后的结果（相当于图2中的A）。

设，取出的硬币为normal硬币为事件B_n;

取出的硬币为double-head硬币为事件B_h；

取出的硬币为double-tail硬币为事件B_t；

硬币落地后正面朝上为事件A_hu；

硬币落地后正面朝下为事件A_hd；

硬币落地后背面朝上为事件A_tu；

硬币落地后背面朝下为事件A_td；

 

a). 需要求P(A_hd)（正面朝下的概率）。取到不同的硬币B_n/B_h/B_t，得到的P(A_hd)也不同，A_hd被分成了三种情况。

由特意可得：

• P(B_n) = 2/5，即从5枚硬币中取到正常硬币的概率；
• P(B_h) = 2/5，即从5枚硬币中取到double-head的概率；
• P(B_t) = 1/5，即从5枚硬币中取到double-tail的概率；
• P(A_hd|B_n) = 1/2，即取到正常硬币时，可以得到正面朝下的概率；
• P(A_hd|B_h) = 1，即取到double-head时，可以得到正面朝下的概率（硬币本身两面都是正面，所以概率为1）；
• P(A_hd|B_t) = 0，即取到double-tail时，可以得到正面朝下的概率（硬币本身两面都是反面，不可能得到正面朝下的情况，所以概率为0）；

由全概率公式，得：

P(A_hd) = P(B_n)*P(A_hd|B_n) + P(B_h)*P(A_hd|B_h) + P(B_t)*P(A_hd|B_t)

           = 2/5*1/2 + 2/5*1 + 1/5*0

           = 3/5

 

b). 根据问题和假设，这里要求解的是条件概率P(A_hd|A_hu)，说明两面都是正面，因此等价于求P(B_h|A_hu)。

参考图2，事件B发生在事件A之前，B有两种情况可能导致A_hu，具体发生了哪种是未知的。（有点像由结果推原因）

由题意可得：

• 可能导致A_hu发生的两种B为：B_n或B_h；
• P(B_n) = P(B_h) = 2/5；
• 参考问题a，可以根据全概率公式计算出A_hu = A_hd = 3/5；
• P(A_hu|B_h) = 1，取到double-head时，可以得到正面朝上的概率（硬币本身两面都是正面，所以概率为1）；

由贝叶斯公式，得：

P(B_h|A_hu) = P(B_h*A_hu)/P(A_hu)

          = P(B_h)*P(A_hu|B_h)/P(A_hu)

          = 2/5 * 1 / (3/5)= 2/3

 

c). 这个问题稍微有点复杂，但也可以分情况讨论：

设该问题——第二次取出的硬币落地后正面朝上，为事件C.

# 第一次分情况

由b)可以知道，b)中取到的硬币只有两种情况(B_n或B_h)，B_n与B_h是一组对立事件。

根据已知的条件，可得：

• 第一次取出的硬币为double-head硬币的概率为P(B_h) = P(B_h|A_hu) = 2/3；
• 第一次取出的硬币为正常硬币的概率为P(B_n) = 1 - P(B_h|A_hu) = 1 - 2/3 = 1/3；
• P(B_n2) =  P(B_h)*P(B_n) + P(B_n)*P(B_n) = 2/3 * 2/4 + 1/3 * 1/4 = 5/12，即第二次取到B_n的概率；
• P(B_h2) =  P(B_h)*P(B_h) + P(B_n)*P(B_h) = 2/3 * 1/4 + 1/3 * 2/4 = 4/12，即第二次取到B_h的概率；
• P(A_hu|B_n2) = 1/2，即第二次取到正常硬币时，可以得到正面朝上的概率；
• P(A_hu|B_h2) = 1，即第二次取到double-head硬币时，可以得到正面朝上的概率；
• 此时的B_h和B_n本质上是在A_hu发生的条件下的条件概率（根据已知的事实计算出来的后验概率），而不再是之前的2/5（先验概率）；

# 第二次分情况

此时的C仍然可以分为两种情况，第二次取到正常硬币或取到double-head硬币。

由全概率公式，得：

P(C) = P(B_n2)*P(A_hu|B_n2) + P(B_h2)*P(A_hu|B_h2) 

        = 5/12 * 1/2 + 4/12 * 1

        = 13/24

 

 

欢迎阅读“概率论与数理统计及Python实现”系列文章

 

 

参考：

---

http://www.cnblogs.com/ohshit/p/5629581.html

edx上的公开课：MITx: 6.008.1x Computational Probability and Inference

《概率论与数理统计》，陈希孺，中国科学技术大学出版社

 

 重大修订版：

• 2017-7-15，添加示意图，补充定义，重新解释了例题的解答过程，补充了例题；