【BZOJ1502】【NOI2005】月下柠檬树 simpson 积分
特别提醒:eps至少要5e-6
首先我们来研究下平行光对投影的影响。
一个二维的图形,若它与光屏平行,那么不论平行光与光屏的夹角为多少,所得图形与原图形全等的(只是位置会有影响)
通过这么一分析,我们将原图形无限切片,并且投影到光屏上去,会发现阴影可以用很多很多个圆的面积并来表示。
这样做显然是T的,我们进行冷静分析(雾)。通过分析得出,阴影为n个圆,n个直角梯形,和一个三角形的并。(如图所示)
在处理的时候,我们可以把三角形当梯形处理。
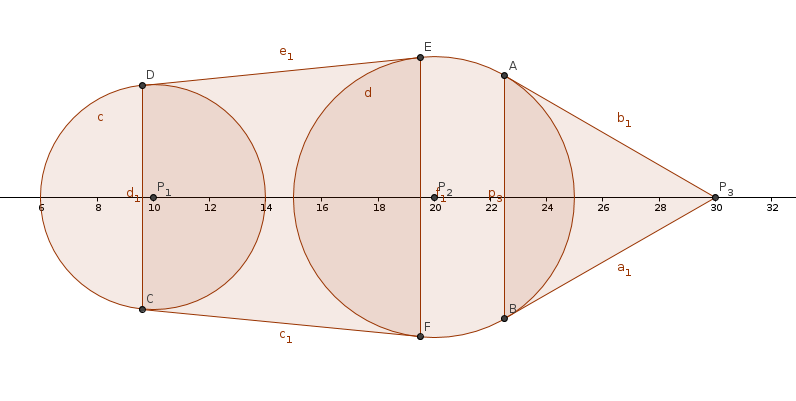
然后就是愉快地Simpson啦~~~~
1 #include<bits/stdc++.h> 2 #define eps 5e-6 3 #define INF 19260817 4 #define M 505 5 using namespace std; 6 double cx[M]={0},cr[M]={0}; 7 double lx[M]={0},rx[M]={0},ly[M]={0},ry[M]={0}; 8 int n; 9 10 double f(double x){ 11 double maxn=0; 12 for(int i=1;i<=n;i++){ 13 double deltax=abs(x-cx[i]); 14 if(deltax>cr[i]) continue; 15 double y=sqrt(cr[i]*cr[i]-deltax*deltax); 16 maxn=max(maxn,y); 17 } 18 for(int i=1;i<n;i++) 19 if(lx[i]<=x&&x<=rx[i]){ 20 double k=(x-lx[i])/(rx[i]-lx[i]); 21 double y=ly[i]+k*(ry[i]-ly[i]); 22 maxn=max(maxn,y); 23 } 24 return maxn; 25 } 26 27 double get(double l,double r){ 28 double mid=(l+r)/2; 29 return (r-l)*(f(l)+4*f(mid)+f(r))/6; 30 } 31 32 double simpson(double l,double r){ 33 double mid=(l+r)/2; 34 double ans1=get(l,r); 35 double ans2=get(l,mid)+get(mid,r); 36 if(fabs(ans2-ans1)<eps) return ans2; 37 return simpson(l,mid)+simpson(mid,r); 38 } 39 40 int main(){ 41 double l=INF,r=-INF,alpha; 42 cin>>n>>alpha; n++; 43 double tana=tan(alpha); 44 for(int i=1;i<=n;i++){ 45 double hh; scanf("%lf",&hh); 46 hh=hh/tana; 47 cx[i]=cx[i-1]+hh; 48 } 49 for(int i=1;i<=n;i++){ 50 if(i!=n)scanf("%lf",cr+i); 51 l=min(l,cx[i]-cr[i]); 52 r=max(r,cx[i]+cr[i]); 53 } 54 for(int i=1;i<n;i++){ 55 double a=cx[i+1]-cx[i]; 56 double b=cr[i+1]-cr[i]; 57 double sita=acos(-b/a); 58 lx[i]=cx[i]+cos(sita)*cr[i]; 59 ly[i]= sin(sita)*cr[i]; 60 rx[i]=cx[i+1]+cos(sita)*cr[i+1]; 61 ry[i]= sin(sita)*cr[i+1]; 62 } 63 double hh=simpson(l,r); 64 printf("%.2lf\n",hh*2); 65 }


