SVM和logistic regression的一些对比

一、SVM的常用目标函数形式

soft margin svm可表示为：

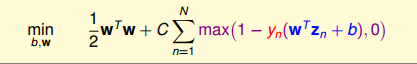
其中，C表示惩罚系数；C越大，表示对margin越严格，即对不满足约束的样本数要更少；

反之，C越小，表示对margin越宽松，即可接受不满足约束的样本数越多。

例如下图所示：

 

二、SVM和logistic regression的对比

1、对于SVM目标函数的解读

SVM的目标函数与带了L2正则的Model的目标函数很相似，并且具有相同的一些性质。

  

 

2、三种常用替代损失函数对比

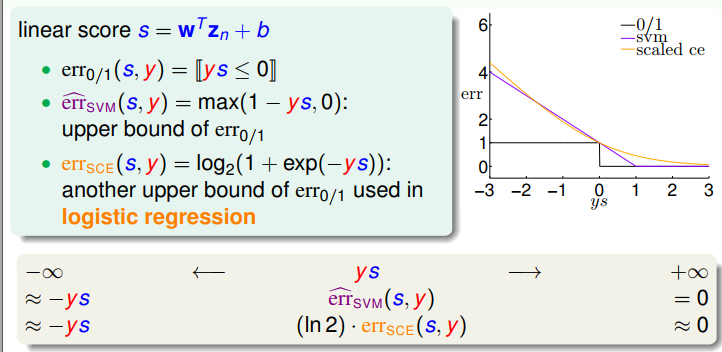
因此，SVM目标函数中的max(1-ys,0)函数与Logistic regression的目标函数很像；如果给LR加入L2正则化，那么有：

 

三、Probabilistic SVM的实现思路

1、鉴于SVM和加L2正则的LR model很相似出发：

（1）idea1

将soft margin的SVM进行求解，将得到的w,b参数当作LR model的w',b'的近似解，然后使用sigmoid函数进行概率求解。

优点：直接使用了svm和LR的相似性，实际使用上，较为简单，通常表现还不错。

缺点：实际上几乎丧失了LR model推导中的maximum likelyhood等性质。

 

 

 

 

 

 

 

 

 

 

（2）idea2

 将soft margin的SVM进行求解，将得到的w,b参数当作LR model解的起始点，再进行LR模型的求解。

缺点：效果和单独使用LR model求解差不多，并且对于kernel svm，则无法使用LR model进行近似。

 

 

2、采用融合SVM和LR各自优势的思路

（1） 做法

      将SVM求解出来的结果（即求解出w和b）后计算(wx+b)的值value，然后在value上加上两个自由度的操作，即放缩操作A，平移操作B；在A和B两个参数上使用logistic regression进行训练（实际上是把A和B分别当作LR model里的w和b参数来求解），这样可以比较吻合在logistic regression中的maximum likelyhood的需求。

优点：保留了svm原有的性质，包括kernel svm的性质；可以使用LR model获得概率值表示。

几何解释：用SVM 找出分类超平面的法向量，然后不改变法向量，但是在法向量之上再加上一些放缩和平移操作，使其更吻合在logistic regression中的maximum likelyhood的需求。

 

（2） Probabilistic SVM的目标函数：

 

 

（3）Probabilistic SVM一般化的求解步骤