强连通分量,割点与桥,Tarjan,双连通分量

强连通分量

强连通指图 \(G\) 中任意两点 \(u,v\) 可以互相到达
强连通分量则是指极大强连通子图

强连通分量的 \(tarjan\) 算法

通过 \(dfs\) 建出原图的生成树(森林)
每个点打上 \(dfs\) 序，并记录其能到达哪个点
\(dfn_u\) 表示 \(u\) 的 \(dfs\) 序/时间戳
\(low_u\) 表示 \(u\) 能到达的点 \(v\) 的最小 \(dfn_v\)

void tarjan(int u){
	stk[++top]=u;
	dfn[u]=low[u]=++DFN;
	for(int i=f[u];i;i=nxt[i]){
		int v=to[i];
		if(!dfn[v]){//--------------------------------未被遍历
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(!col[v]){//---------------------------在搜索栈中，此处用col数组兼用了vis的作用
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]){
		col[u]=++cntcol;
		while(stk[top]!=u)col[stk[top--]]=cntcol,++tot[cntcol];
        top--;
	}
}

割点

割点是无向图中删掉后强连通分量数量增加的点
桥(割边)是同效的边
\(dfn,low\) 同上
\(low_u\) 即为 \(u\) 不经过父亲能到达的最小时间戳
所以 \(low_v \le low_u\) 的点即为割点 ( \(v\) 为 \(u\) 儿子)

割点的 \(tarjan\) 算法

void tarjan(int u,int rt){
	dfn[u]=low[u]=++DFN;
	int son=0;
	for(int i=f[u];i;i=nxt[i]){
		int v=to[i];
		if(!dfn[v]){
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
			if(rt!=u&&low[v]>=dfn[u])cutP[u]=1;
			++son;
		}
		low[u]=min(dfn[v],low[u]);
	}
	if(son>=2&&u==rt)cutP[u]=1;
}

边双连通分量与桥

图无向 \(G\) 中，若点 \(u,v\) 在删掉任意一条边后 \(u,v\) 仍联通，则 \(u,v\) 是边双连通分量
若删掉点则为点双连通分量
其中边双连通分量有传递性
而点双连通分量没有，如： \((x,y),(y,z)\) 为点双连通分量， \(y\) 为割点从而 \((x,z)\) 不一定为点双连通分量

边双连通分量的求法1.

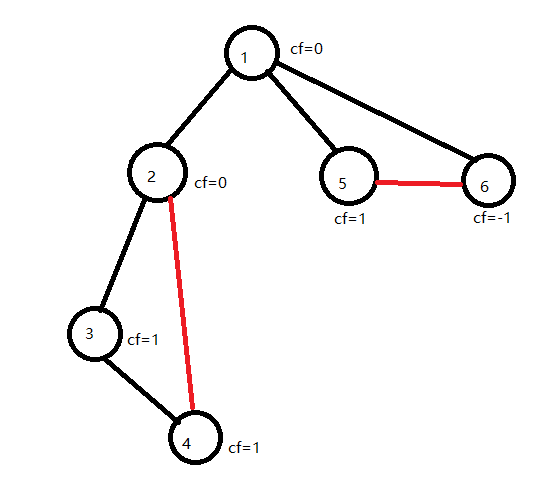
图1

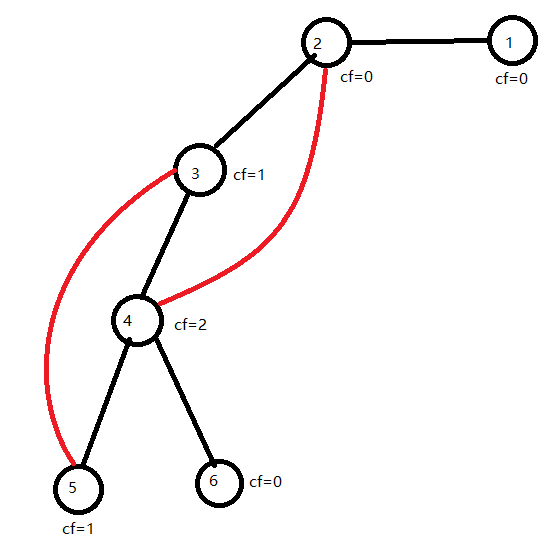
图2
黑色为树边，红色为非树边
通过 \(dfs\) 建立生成树，给非树边深度大的点打上差分+1，深度小的打上-1。
若一个点其子树差分之和为0，即没有非树边跨过此点，则其和其父亲的连边即为桥。
可以看出，上图1的 2 号点，\(cf_2=0\) 可以看出，没有非树边跨过此点，所以 \(Edge_{1,2}\) 为桥。
图2的 3 号点，\(cf_3=1\) ，所以有1条非树边跨过此点，所以 \(Edge_{2,3}\) 不为桥。
若 \(u,v\) 两点树上路径没有桥，则其为边双连通分量。
P8436
这个方法常数比较大，此题亦可通过 \(tarjan\) 处理

#include<iostream>
using namespace std;
const int N=5e5+50;
const int M=2e6+50;
const int lgN=22;
int n,m,q;
int f[N],fr[M<<1],to[M<<1],nxt[M<<1],cnt=1;//--------前向心，cnt=1方便管理双向边
bool mrk[M<<1],brg[M<<1],vis[N],vs[N];
int dep[N],cf[N];
int fl[N],cntfl;
void add(int u,int v){nxt[++cnt]=f[u];f[u]=cnt;to[cnt]=v;fr[cnt]=u;}
void dfs0(int u,int ft){//--------预处理dep，标记树边
	dep[u]=dep[ft]+1;
	vis[u]=1;
	for(int i=f[u];i;i=nxt[i]){
		int v=to[i];
		if(v==ft)continue;
		if(!vis[v]){
			mrk[i]=mrk[i^1]=1;
			dfs0(v,u);
		}
	}
}
void dfs1(int u,int ft){//--------计算差分，标记桥
	vis[u]=0;
	for(int i=f[u];i;i=nxt[i]){
		if(!mrk[i])continue;
		int v=to[i];
		if(v==ft)continue;
		dfs1(v,u);
		cf[u]+=cf[v];
		if(cf[v]==0)brg[i]=brg[i^1]=1;
	}
}
void dfs3(int u){//--------遍历双连通分量
	vs[u]=1;
	fl[++cntfl]=u;
	for(int i=f[u];i;i=nxt[i]){
		if(brg[i])continue;
		int v=to[i];
		if(!vs[v])dfs3(v);
	}
}
int main(){int x,y,ans=0,tmp=0;
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++){cin>>x>>y;if(x^y){add(x,y);add(y,x);}}
	for(int i=1;i<=n;i++)if(!vis[i])dfs0(i,0),++ans;//--------不同连通块属于不同双连通分量--->>>++ans
	for(int i=2;i<=cnt;i+=2)
        if(!mrk[i])
            cf[dep[fr[i]]<dep[to[i]]?fr[i]:to[i]]+=-1,
            cf[dep[fr[i]]<dep[to[i]]?to[i]:fr[i]]+=1;
	for(int i=1;i<=n;i++)if(vis[i])dfs1(i,0);
	for(int i=2;i<=cnt;i+=2)if(brg[i])++ans;//--------桥把一个连通块分开成不同双连通分量
	cout<<ans<<endl;//---------输出双连通分量数量
	for(int u=1;u<=n;u++)if(!vs[u]){
        cntfl=0;
        dfs3(u);
        cout<<cntfl<<' ';//输出双连通分量
        for(int i=1;i<=cntfl;i++)cout<<fl[i]<<' ';
        cout<<endl;
    }
	return 0;
}

桥与边双连通分量的 \(tarjan\) 算法

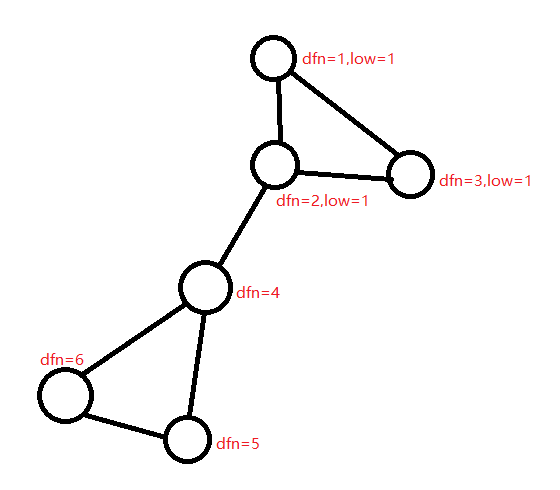
搜索完 \(dfn=4\) 的子树，发现其 \(low=4\) 即不能不通过其父亲下来的边到达 \(dfn\) 更小的点，即其与其父亲只有一条路径，即其与其父亲的边为桥
而桥又把图分为不同的边双连通分量

void tarjan(int u,int ft){//------------几乎与强连通分量的tarjan算法一模一样
	dfn[u]=low[u]=++DFN;
	stk[++top]=u;
	for(int i=f[u];i;i=nxt[i]){
		int v=to[i];
		if(v==ft)continue;//------------不能通过父亲到达的时间戳最小的点
		if(!dfn[v]){
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u])brg[i]=brg[i^1]=1;//------------brg储存桥
		}
		else if(!col[v])low[u]=min(low[u],dfn[v]);//------------col兼用vis的功能
	}
	if(dfn[u]==low[u]){
		++pn[col[u]=++cntcol];
		while(stk[top]!=u)++pn[col[stk[top--]]=cntcol];
		top--;
	}
}

若有重边，则可传入从父亲下来的边的编号

void tarjan(int u,int ec){
	low[u]=dfn[u]=++DFN;
	stk[++top]=u;
	for(int i=f[u];i;i=nxt[i]){
		int v=to[i];
		if(i==(ec^1))continue;
		if(!dfn[v]){
			tarjan(v,i);
			low[u]=min(low[u],low[v]);
			if(low[v]>dfn[u])brg[i]=brg[i^1]=1;
		}
		else if(!col[v])low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u]){
		col[u]=++cntc;
		while(stk[top]!=u)col[stk[top--]]=cntc;
		--top;
	}
}

废案

int a[N<<1],Eun,fir[N],lg[N<<1],RMQ[N<<1][lgN],cntbrg[N];
void initRMQ(){
	for(int i=1;i<=Eun;i++)RMQ[i][0]=a[i];
	for(int j=1;j<=lg[Eun];j++)for(int i=1;i<=Eun-(1<<j)+1;i++){
		int x=RMQ[i][j-1],y=RMQ[i+(1<<(j-1))][j-1];
		RMQ[i][j]=dep[x]<dep[y]?x:y;
	}
}
void dfs2(int u,int ft){
	for(int i=f[u];i;i=nxt[i]){
		if(!mrk[i])continue;
		int v=to[i];
		if(v==ft)continue;
		cntbrg[v]=cntbrg[u]+(brg[i]==1);
		dfs2(v,u);
	}
}
int lca(int u,int v){
	int l=fir[u],r=fir[v];if(l>r)swap(l,r);
	int x=lg[r-l+1],y1=RMQ[l][x],y2=RMQ[r-(1<<x)+1][x];
	return dep[y1]<dep[y2]?y1:y2;
}
int chk(int u,int v){return cntbrg[u]+cntbrg[v]-2*cntbrg[lca(u,v)];}
int main(){
    int x,y;
	ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
	cin>>n>>m>>q;
	for(int i=1;i<=m;i++){
        cin>>x>>y;
        add(x,y);add(y,x);
    }//--------前向心建图
	dfs0(1,0);//--------处理dep,记录树边
	lg[0]=-1;for(int i=1;i<=Eun;i++)lg[i]=lg[i>>1]+1;initRMQ();//--------St表预处理lca
	for(int i=2;i<=cnt;i+=2)
        if(!mrk[i])
            cf[dep[fr[i]]<dep[to[i]]?fr[i]:to[i]]=-1,//--------深度小的点打上-1的差分
            cf[dep[fr[i]]<dep[to[i]]?to[i]:fr[i]]=1;//--------深度大的点打上+1的差分

	dfs1(1,0);//--------处理出桥
	dfs2(1,0);//--------预处理路径上桥的个数
	for(int i=2;i<=cnt;i+=2)if(brg[i])cout<<fr[i]<<"<->"<<to[i]<<endl;//--------输出桥
	while(q--){
		cin>>x>>y;
		cout<<chk(x,y)<<endl;
	}
	return 0;
}

posted @ 2024-07-19 11:52 Xie2Yue 阅读(29) 评论(0) 收藏举报

刷新页面返回顶部

Xie2Yue

Xie2Yue

强连通分量,割点与桥,Tarjan,双连通分量