哈夫曼树和哈夫曼编码
当树中的节点被赋予一个表示某种意义的数值，我们称之为该节点的权。从树的根节点到任意节点的路径长度(经过的边数)与该节点上权值的乘积称为该节点的带权路径长度。树中所有叶节点的带权路径长度之和称为该树的带权路径长度(WPL)。当带权路径长度最小的二叉树被称为哈夫曼树，也成为最优二叉树。
如下图所示，有三课二叉树，每个树都有四个叶子节点a，b，c，d，分别取带权7，5，2，4。他们的带权路径长度分别为
(a) WPL = 7x2+5x2+2x2+4x2=36
(b) WPL = 2X1+4X2+7X3+5X3 = 46
(c) WPL = 7x1+5x2+2x3+4x3 = 35
节点如果像c中的方式分布的话，WPL能取最小值(可证明)，我们称为哈夫曼树。
哈夫曼树构造
哈夫曼树在构造时每次从备选节点中挑出两个权值最小的节点进行构造，每次构造完成后会生成新的节点，将构造的节点从备选节点中删除并将新产生的节点加入到备选节点中。新产生的节点权值为参与构造的两个节点权值之和。举例如下：
- 备选节点为a,b,c,d，权值分别为7,5,2,4
- 选出c和d进行构造(权值最小),生成新节点为e(权值为6)，备选节点变为7,5,6
- 选出b和e进行构造，生成新节点f(权值为11),备选节点为7,11
- 将最后的7和11节点进行构造，最后生成如图所示的哈夫曼树
哈夫曼树应用
在处理字符串序列时，如果对每个字符串采用相同的二进制位来表示，则称这种编码方式为定长编码。若允许对不同的字符采用不等长的二进制位进行表示，那么这种方式称为可变长编码。可变长编码其特点是对使用频率高的字符采用短编码，而对使用频率低的字符则采用长编码的方式。这样我们就可以减少数据的存储空间，从而起到压缩数据的效果。而通过哈夫曼树形成的哈夫曼编码是一种的有效的数据压缩编码。
如果没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码。如0,101和100是前缀编码。由前缀码形成的序列可以被唯一的组成一个字符串序列。如00101100可以被唯一的分析为0，0，101和100。
示例:
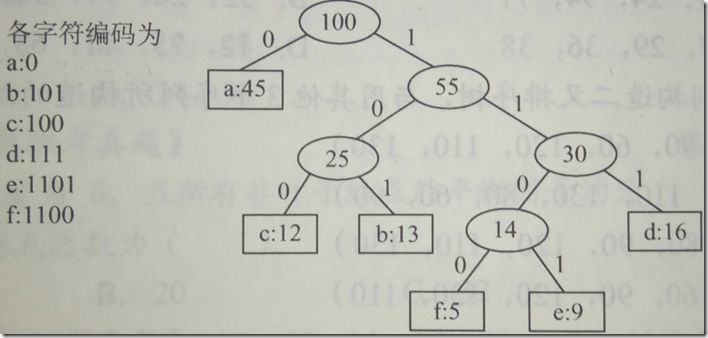
我们对一个字符串进行统计发现a-f出现的频率分别为a:45，b:13，c:12，d:16，e:9，f:5，我们对该字符串进行采用哈夫曼编码进行存储。
WPL = 1x45+3x(13+12+16)+4x(5+9)=224
这样算下来使用224二进制位就可以将该字符串存储起来，因为哈夫曼码是前缀码，所以可以唯一的还原出原来的字符序列。如果我们每个字符使用3位进行存储(至少3位),那么需要300bit才能将该字符串存储下。
