一、MySQL Index 的插入
有如下B+树,其高度为2,每页可存放4条记录,扇出为5。所有记录都在叶子节点上,
并且是顺序存放,如果用户从最左边的叶子节点开始顺序遍历,可以得到所有简直的顺序
排序:5、10、15、20、25、30、50、55、60、65、75、80、85、90。

B+树的插入操作,分为三种情况

1、Leaf Page和Index Page都没满
用户插入28这个值,Leaf Page和Index Page都没满,直接插入即可
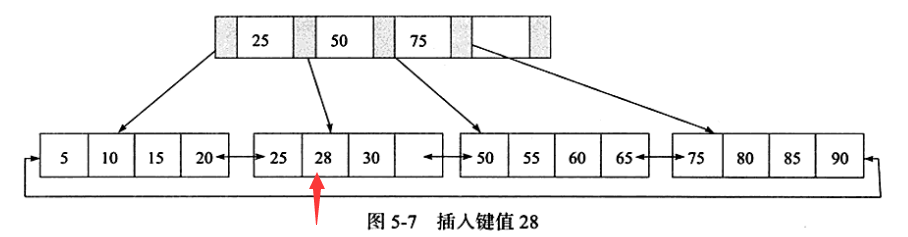
2、Leaf Page已经满了,Index Page没有满
用户插入70这个值,Leaf Page已经满了,Index Page没有满。
这是插入Leaf Page后情况为50、55、60、65、70,并根据中间值60来拆分叶节点。
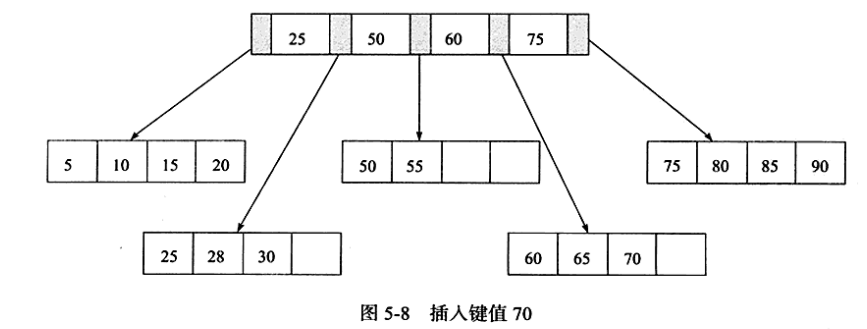
3、Leaf Page和Index Page都满了
插入95这个值,Leaf Page和Index Page都满了,这是需要两次拆分
1)首先插入Leaf Page后情况为75、80、85、90、95,由于Leaf Page已经满了,需要根据中间值85拆分叶节点,小于85的放左边即75、80;
大于等于85的放右边即85、90、95。
2)将中间节点85放入Index Page后,Index Page的值为25、50、60、75、85,由于Index Page也满了,需要拆分Index Page,取中间值60,
放入上层Index Page中,小于60的25、50放在左边;大于60的值75、85放在右边。
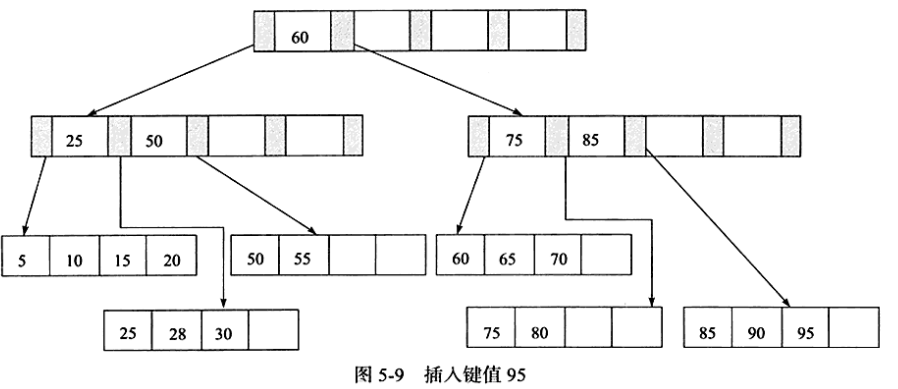
4、B+树的旋转(继承平衡二叉树的旋转功能)
不管怎么变化B+树总是保持平衡。但是为了保持平衡杜宇先插入的键值可能需要做大量的拆分操作。因为B+树结构主要用于磁盘,页的拆分意味着磁盘操作,所以应该在可能的情况下尽量减少页的拆分操作。因此,B+树同样提供了类似平衡二叉树的旋转(Rotation)功能。
旋转发生在Leaf Page已满,其左右兄弟没满的情况下。B+树不急于做拆分,通常情况下左兄弟会被首先检查用来做旋转操作。

插入键值70,其实B+树并不会急于去拆分叶子节点,而是去做旋转操作,得到如图
采用旋转操作使得B+树减少了一次页的拆分操作,同时B+树的高度依然是2。
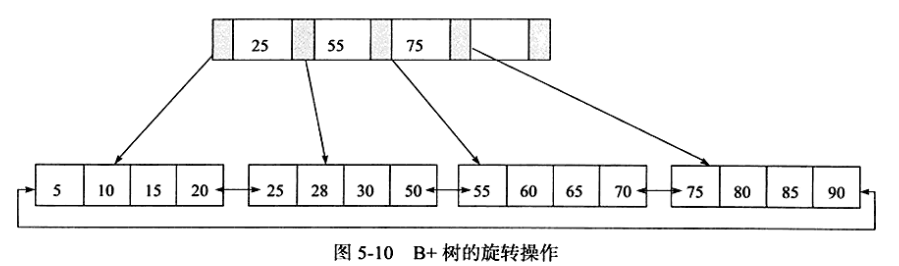
二、MySQL Index 的删除
B+树使用填充因子(fill factor)来控制树的删除变化,50%是填充因子可以设置的最小值。B+树的删除操作同样必须保证删除后叶子节点中的记录依然排序,同插入一样,B+树的删除操作同样有三种情况,与插入不同的是,删除时根据填充因子的变化衡量。
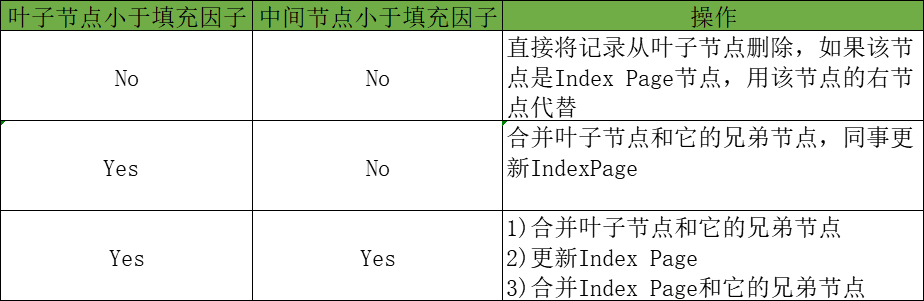

1、叶子节点大于填充因子、中间节点大于填充因子
1)删除键值为70的这条记录,该记录符合第一种情况,删除后可得下图

2)接着5-11,再删除键值为25的记录,这也是讨论的第一种情况,但是该值是Index Page中的值,因此在删除Leaf Page中的25后,还应该将25的兄弟节点的28更新到Page Index中。
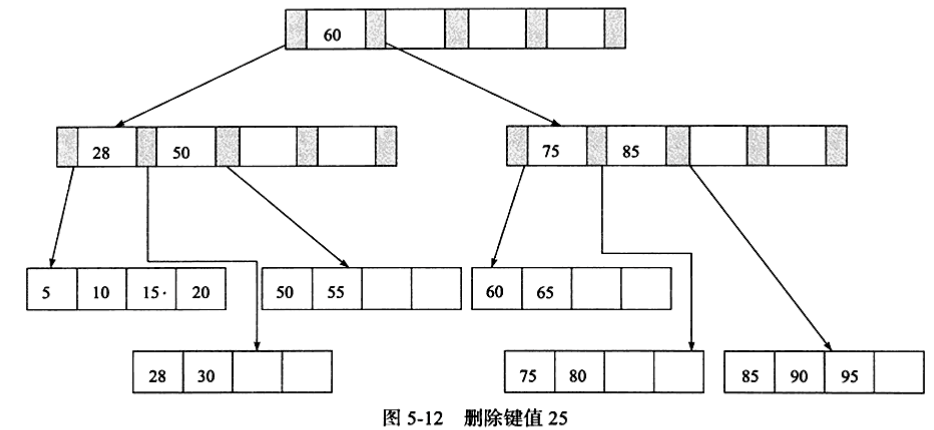
2、叶子节点小于填充因子、中间节点大于填充因子
3、叶子节点小于填充因子、中间节点小于填充因子
最后删除键值60的情况。删除Leaf Page中键值为60的记录后,Fill Factor小于50%,这时需要做合并操作,同样,再删除Index Page中相关记录后,需要做Index Page的合并操作,最后如图
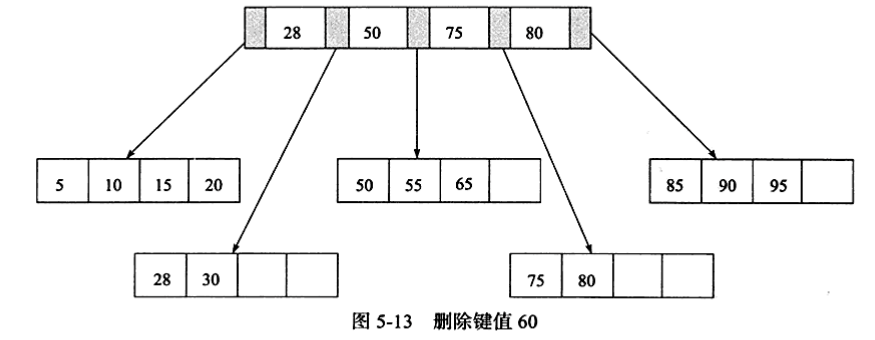
三、一些概念
1、索引扇出
扇出:是指该模块直接调用的下级模块的个数。扇出大表示模块的复杂度高,需要控制和协调过多的下级模块;但扇出过小(例如总是1)也不好。
扇出过大一般是因为缺乏中间层次,应该适当增加中间层次的模块。扇出太小时可以把下级模块进一步分解成若干个子功能模块,或者合并到它的上级模块中去。
2、索引填充因子
和索引重建最相关的是填充因子。当创建一个新索引,或重建一个存在的索引时,你可以指定一个填充因子,它是在索引创建时索引里的数据页被填充的数量。填充因子设置为100意味着每个索引页100%填满,50%意味着每个索引页50%填满。
如果你创建一个填充因子为100的聚集索引(在一个非单调递增的列上),那意味着每当一个记录被插入(或修改)时,页拆分都会发生,因为在现存的页上没有这些数据的空间。



 posted on
posted on

