PCA-主成分分析的原理及解释
主成分分析(principal component analysis,PCA)
PCA利用正交变换将线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据。
线性无关的变量称为主成分,其个数通常小于原始变量的个数,所以属于无监督学习中的降维方法。
一、PCA的解释—最大方差理论

由上图可以看到,$x_{1}$和$x_{2}$两个变量之间具有线性相关性。已知其中一个变量$x_{1}$的取值时,对另一个变量$x_{2}$的预测不是完全随机的,反之亦然。
为了减少这种相关性,我们对坐标系进行旋转变换(正交变换),将数据投影到新坐标系的坐标轴上,那如何选择坐标系呢?
我们将数据在每一轴上的坐标值的平方表示相应变量的方差,并且这个坐标轴上的方差是最大的(在所有可能的新坐标系中)。找到第一坐标轴后,然后选择与第一坐标轴正交,且方差次之的方向作为第二坐标轴,如上图(b)。
主成分分析旨在选取正交变换中方差最大的变量,那为什么方差最大,变量之间的相关性越小?
答:数据在某个方向上的轴的方差越大,那么说明数据分布得更为分散,相关性越小。在信号处理领域,信号具有较大的方差,噪声具有较小的方差,信号与噪声之比称为信噪比。而信噪比越大,意味着数据的质量越好。
回忆一下,线性代数的相关内容?
- 正交矩阵:满足条件$\boldsymbol{A}^{T}\boldsymbol{A}=\mathbf{E}$或者$\boldsymbol{A}\boldsymbol{A}^{T}=\mathbf{E}$的n阶方阵称为正交矩阵。
- 判定正交矩阵的充分必要条件为:A的列(行)向量都是单位向量,且两两正交。
- 设A为正交矩阵,则线性变换$\mathbf{y} =\boldsymbol{\mathbf{} Ax}$称为正交变换。正交变换保证向量的内积和长度不变,具有保形性。
回忆一下,协方差和相关系数的知识?
- 协方差和相关系数都可以用来描述两个分量之间相互关系的数字特征。
- 协方差$Cov\left ( X,Y \right )=E[\left ( X-EX \right )\left ( Y-EY \right )]$。
- 相关系数$\rho _{XY}=\frac{Cov\left ( X,Y \right )}{\sqrt{DX}\cdot \sqrt{DY}}$。
- 相关系数(协方差)变大,X与Y的线性相关程度就变大。
推导:





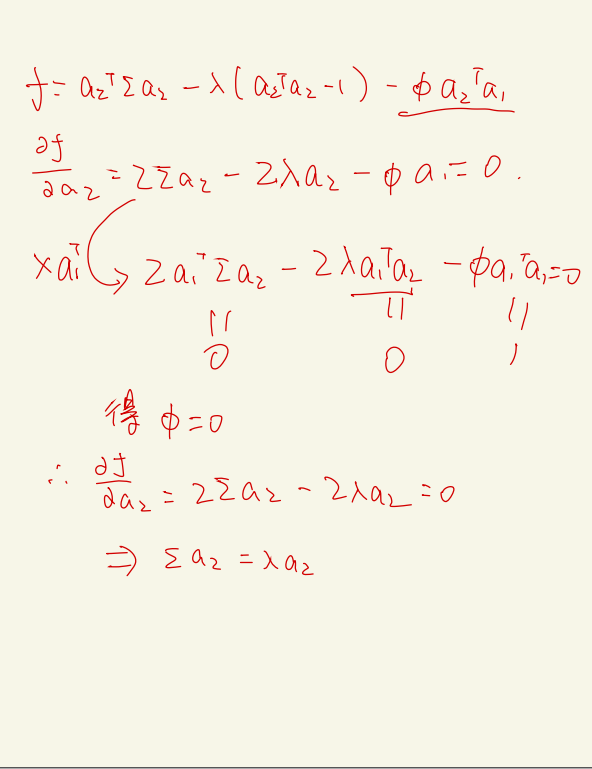

矩阵和向量求导的相关公式::


作者:Ryanjie
出处:http://www.cnblogs.com/ryanjan/
本文版权归作者和博客园所有,欢迎转载。转载请在留言板处留言给我,且在文章标明原文链接,谢谢!
如果您觉得本篇博文对您有所收获,觉得我还算用心,请点击右下角的 [推荐],谢谢!

