Swin Transformer
一、大体内容
PDF:https://arxiv.org/pdf/2103.14030
CODE:https://github.com/microsoft/Swin-Transformer
前面提出的ViT将Transformer引入到了视觉领域,但其重点解决了分类问题,其采用单一尺度提取特征对后续目标检测和分割等任务不太友好。Swin Transformer人为Transformer可以作为视觉的一个通用框架,而不仅仅是分类,但目标检测、分割等任务需要学习到至关重要的多尺度特征,比如目标检测通常采用特征金字塔,分割采用UNET这种跳跃连接的操作来获取多尺度特征,Swin Transformer提出采用层级结构,提出了多尺度的Transformer结构,但随着图片分辨率的增大,计算量增长较快,Swin Transformer采用Shifted和Windows的方法来提升计算效率(Swin= S + win),为视觉领域应用提供了一个全新的骨架网络。在COCO目标检测和ADE20K语义分割任务上取得了很好的效果。
整体结构和流程
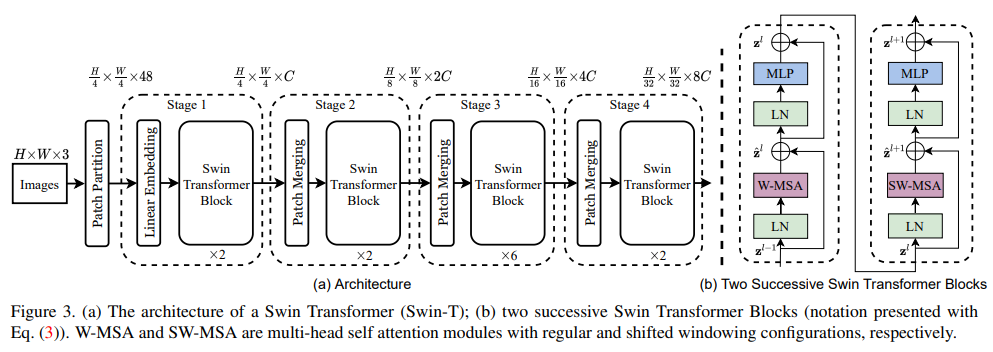
整体结构上类似于ResNet,图像分辨率减小的同时,通道数增加,只是内部块采用了Swin Transformer结构。输入图像先划分成大小为44的patch,特征维度由变为,48=443,然后经过一个线性层得到特征编码得到特征维度是,由于Swin Transformer结构不改变输入维度,所以输出仍然是;相邻patch进行merge,类似于池化操作,图像分辨率变为,相应的特征通道数变为,为了和ResNet结构一致,通过一个11的卷积将通道数变为,也就维持了图片分辨率减半的同时保证通道数翻倍,依此类推,最终特征维度变为。注意这里没有像ViT一样采用一个特殊编码把特征维度增加由196变为197,这里直接采用全局平均对其进行处理,可能两者对齐的不一样(ViT主要是和Transformer对比,而Swin Transformer主要是对齐ResNet)。
还提供了不同大小的模型,也就是各层的数量不一样。
Swin-T: C = 96, layer numbers={2, 2, 6, 2}
Swin-S: C = 96, layer numbers={2, 2, 18, 2}
Swin-B: C = 128, layer numbers={2, 2, 18, 2}
Swin-L: C = 192, layer numbers={2, 2, 18, 2}
二、贡献点
- 提出一种层级形式的Transformer结构,可以作为视觉任务的通用骨架网络
- 提出Shifted Windows操作,加速了计算效率的同时还允许跨窗口进行自注意力机制,进而提取全局特征
- 提出patch merge,改变特征尺度类似于CNN中的pooling操作
- 在ImageNet-1K,COCO,ADE20K等数据集上都取得了很好的效果
三、细节
3.1 层级结构
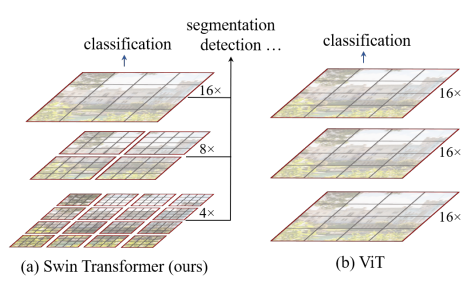
ViT始终采用同一个大小的patch进行,而Swin Transformer先采用较小的patch,然后patch之间进行合并操作,能提取到不同尺度的特征,这对目标检测和分割至关重要。
- Patch Merge
经过Patch Merging后,feature map的高和宽会减半,深度会加倍(原本是4倍,为了和ResNet对齐,经过一个1x1的卷积变换到2倍),图片来源于Patch Merging
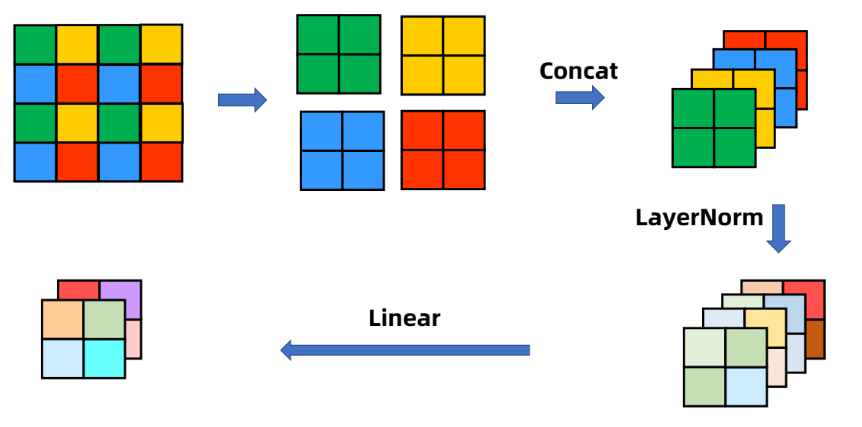
3.2 带窗口的自注意力模式
带窗口的自注意一方面是可以提取不同尺度大小patch的特征,另一个方面是计算量相对于原有的多头注意力(MSA)较小,有利于提高计算效率。
文中给出了计算量的大致估计:

一般的多头注意力计算量是(1)式,带窗口的是(2)式,虽然第一项相同,但是第二项M表示块的大小,相比于原图宽高要小很多。
- 计算量估计流程

以上图为参考,方框下方表示其维度信息,原始输入特征为f: ,最终输出特征f''也为 。
得到q, k, v,相当于要乘一个 的权重矩阵,即:,这里有三个,所以计算量大约为;
然后q和k相乘得到相关矩阵A,即,这一步计算量约:;
v和A进行计算得到f',即,这一步计算量约:;
最后在进行一个特征投射得到f'',即,计算量为:。
上面几步进行求和即可得到(1)式的计算量。
带窗口的计算量如下:
单个窗口大小为M*M,带入(1)式可以得到 ,窗口一共有个,两者相乘即可得到(2)式。
3.3 shifted方式

采用向右下角偏移的策略,这样可以使得原先不重叠的窗口之间可以进行交互,窗口之间可以进行交互,自注意力机制就有了全局建模能力。
这种方式虽然可以让窗口之间进行交互,但是会导致每个窗口的大小不一致且窗口数量增加,如果采取不足的位置补零,那么计算量就会增加,作者设计了一种shift mask策略(见3.4)来保证计算量不变的情况下可以得到相应的特征。
3.4 shift mask策略
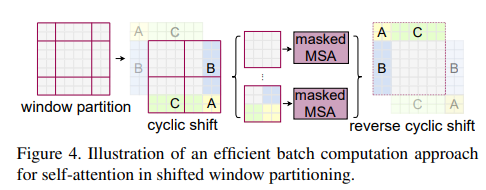
上图展示了shift mask策略,首先将窗口进行进行旋转偏移,即B,A,C分别补到对应位置,构成原有大小的patch。这样计算量就不会增加,但也带来了另外一个问题,就是随着位置改变,比如C区域原本在上方,但变到下方后,直接进行特征提取会存在问题(比如:脸部区域,眼睛本身在上方,但这样调整后会位于下方,那这种对学习的特征会有影响),因此作者针对不同情形提出了对应的掩码如下。然后把掩码和最终结果进行相加,不应该有的区域给一个非常小的权重,这样就实现了一次推理得到结果,并没有增加计算量。

参考:https://github.com/microsoft/Swin-Transformer/issues/38
3.4 Swin Transformer Block

左侧是经过带窗口的注意力,然后再进行Shift后进行自注意力,由于两个是一起的,因此可以看到网络结构中块的数量都是偶数。

3.4 相对位置编码
注意这里和NLP中不一样的地方在于NLP是把位置编码加载QKV之前,而这里是QKV之后加入位置编码
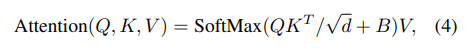
试验结果表明相对位置编码效果最好。

这一块更多内容可以参考:https://www.zhihu.com/tardis/zm/art/577855860?source_id=1005
四、效果
分类效果
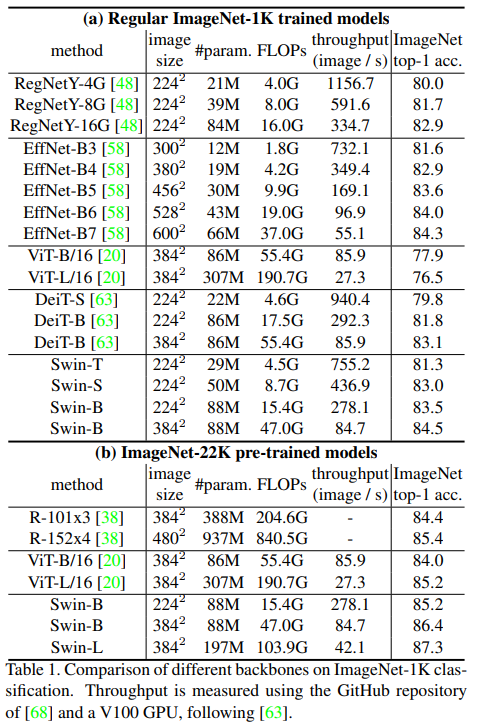
检测效果

分割效果






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!