最小二乘法拟合空间直线
一、空间直线方程
1.1 一般方程
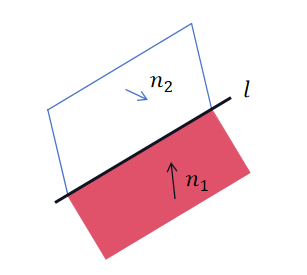
空间直线可以看成成两个平面的交线，设两个平面方程分别为\(A_1x + B_1y + C_1z + D_1 = 0\) 和 \(A_2x + B_2y + C_2z + D_2 = 0\)，则直线\(l\)的一般方程可以表示为：
\(\left\{\begin{matrix}
A_1x + B_1y +C_1 +D_1 = 0
\\
A_2x + B_2y +C_2 +D_2 = 0
\end{matrix}\right.\)
1.2 点向式
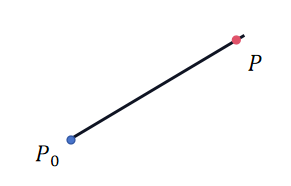
设直线方向向量为\(v = (m, n, t)\)，直线上一点\(P_0：（x_0, y_0, z_0）\)，则任意点\(P:(x, y, z)\)可以表示为 \(P = kP_0\)，所以直线也可以表示为：
\(\frac{x - x_0}{m} = \frac{y - y_0}{n} = \frac{z - z_0}{t} = k\)
1.3 参数式
点向式经过简单变形即可得到：
\(\left\{\begin{matrix}
x = x_0 + mk
\\
y = y_0 + nk
\\
z = z_0 + tk
\end{matrix}\right.\)
1.4 平面法线叉乘表示
设两平面法线分别为：\(n_1=(x_1, y_1, z_1)\) 和 \(n_2 = (x_2, y_2, z_2)\)，则直线的方向向量\(v(i,j,k)\)可以表示为：
\(v = n_1 \times n_2 = \begin{vmatrix}
i & j & k \\
x_1 & y_1 & z_1 \\
x_2 & y_2 & z_2
\end{vmatrix}\)
在到直线上取一点即可表示直线。
二、公式推导
这里参考链接1给出基于最小二乘法拟合直线的推导，设直线点向式方程为：\(\frac{x - x_0}{m} = \frac{y - y_0}{n} = \frac{z - z_0}{t}\)，则转换后可以得到
\(\left\{\begin{matrix} x = \frac{m}{t}(z - z_0) + x_0 = k_1z + b1 \\ y = \frac{n}{t}(z-z_0) + y_0 = k_2z + b_2 \end{matrix}\right.\)
其中\(K_1 = \frac{m}{t}, b_1 = x_0 - \frac{m}{t} z_0, k_2 = \frac{n}{t}, b_2 = y_0 - \frac{n}{t}z_0\)。
所以空间直线可以看作
\(\left\{\begin{matrix} x = k_1z + b1 \\ y = k_2z + b_2 \end{matrix}\right.\)
两个平面相交，因此对空间之间拟合就可以转换为对这两个平面的拟合，假设有\(n\)个点\((x_1, y_1, z_1), (x_2, y_2, z_2),...,(x_n, y_n,z_n)\)，则可以得到这些点和两个平面的残差的平方和为：
\(\left\{\begin{matrix} Q_1 = \sum_{i = 1}^{n}(x_i - k_1z_i -b_1)^2 \\ Q_2 = \sum_{i = 1}^{n}(y_i - k_2z_i -b_2 )^2 \end{matrix}\right.\)
依据最小二乘法有：\(Min Q_1\) 和 \(Min Q_2\)，因此分别对\(k_1, b_1, k_2, b_2\)求导，然后令导数为0可以得到：
\(\left\{\begin{matrix} \sum_{i = 1}^{n}2(x_i - k_1z_i -b_1)(-z_i) = 0 \\ \sum_{i = 1}^{n}2(x_i - k_1z_i -b_1)(-1) = 0 \\ \sum_{i = 1}^{n}2(y_i - k_2z_i -b_2)(-z_i) = 0 \\ \sum_{i = 1}^{n}2(y_i - k_2z_i -b_2)(-z_i) = 0 \end{matrix}\right.\)
依据第一个式子有：
\(\sum_{i=1}^{n}(-x_iz_i - k_1z_i^2+b_iz_i)=0\)
==>
\(k_1 = \frac{\sum_{i=1}^{n}x_iz_i - \sum_{i=1}^{n}b_iz_i}{\sum_{i=1}^{n}z_i^2}\)
依据第二个式子有：
\(b_1 = \frac{\sum_{i=1}^{n}x_i - k_1 \sum_{i=1}^{n}z_i}{n}\)
将\(b_1\)代入\(k_1\)中可以得到：
\(k_1 = \frac{n\sum_{i=1}^{n}x_iz_i - \sum_{i=1}^{n}x_i\sum_{i=1}^{n}z_i}{n\sum_{i=1}^{n}z_i^2 - \sum_{i=1}^{n}z_i\sum_{i=1}^{n}z_i}\)
同理可以得到：
\(k_2 = \frac{n\sum_{i=1}^{n}y_iz_i - \sum_{i=1}^{n}y_i\sum_{i=1}^{n}z_i}{n\sum_{i=1}^{n}z_i^2 - \sum_{i=1}^{n}z_i\sum_{i=1}^{n}z_i}\)
\(b_2 = \frac{\sum_{i=1}^{n}y_i - k_2 \sum_{i=1}^{n}z_i}{n}\)
求出\(k_1,k_2,b_1,b_2\)后就可以算出直线的方向向量\(v=(m, n, t)\)，令\(t = 1\)，则\(m = k_1, n = k_2\)，所以\(v(k_1, k_2, 1)\)，还可以求出直线上一个点\(p(x, y, z)\) ,令\(z = 1\)，则\(x = k_1 + b_1, y = k_2 + b_2\)，所以点坐标可以表示为：\(p(k_1 + b_1, k_2 + b_2, 1)\)。
三、代码实现
double FitLine(const std::vector<Vector3>& pointArray, Vector3& dir, Vector3& pt)
{
// ref: https://www.doc88.com/p-8189740853644.html
core::Vector3 center = core::Vector3(0.0, 0.0, 0.0);
int n = pointArray.size();
for (const core::Vector3& pt : pointArray) {
center += pt;
}
double sumXZ = 0.0, sumYZ = 0.0, sumZ2 = 0.0;
for (const core::Vector3& pt : pointArray) {
sumXZ += pt.x() * pt.z();
sumYZ += pt.y() * pt.z();
sumZ2 += pt.z() * pt.z();
}
double den = n * sumZ2 - center.z() * center.z();
double k1 = (n * sumXZ - center.x() * center.z()) / den;
double b1 = (center.x() - k1 * center.z()) / n;
double k2 = (n * sumYZ - center.y() * center.z()) / den;
double b2 = (center.y() - k2 * center.z()) / n;
dir = core::Vector3(k1, k2, 1.0);
dir.Normalize();
double z = 1.0;
double x = k1 + b1;
double y = k2 + b2;
pt = core::Vector3(x, y, 1.0);
return 0.0;
}
四、效果
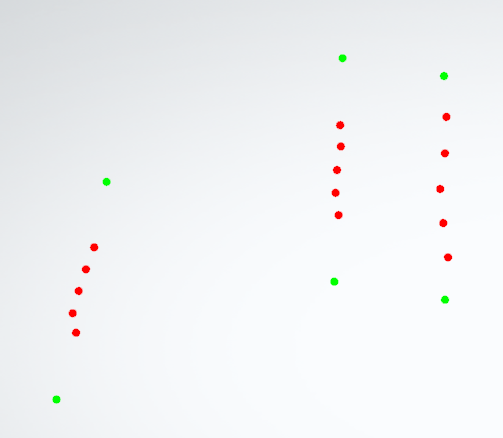
下面是拟合的效果，红色点是输入散点，绿色点表示直线上的两个点。
