Self Attention
先前的一些文章简单介绍了一些点云检测和分割的文献资料,可以看出近些年越来越多的方法结合了Transformer,因此有必要说明一下Transformer的结构,在介绍之前需要了解一些知识点:比如Self Attention、Layer Normalization等等,这一篇先简单了解下Self Attention,后续再介绍其他相关内容。本文先简单介绍Attention的发展,然后介绍self Attention的内容与具体例子,再介绍其和CNN、RNN的区别与后续改进工作。
一、大致发展
这里主要在注意力机制发展历程新增了Transformer。
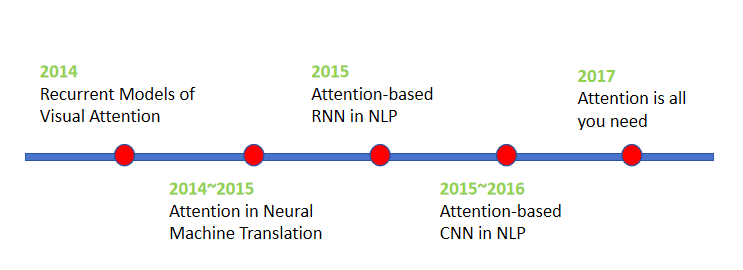
Attention机制最早是在视觉图像领域提出来的,应该是在九几年思想就提出来了,但是真正火起来应该算是google mind团队的这篇论文《Recurrent Models of Visual Attention》,他们在RNN模型上使用了attention机制来进行图像分类。随后,Bahdanau等人在论文《Neural Machine Translation by Jointly Learning to Align and Translate》中,使用类似attention的机制在机器翻译任务上将翻译和对齐同时进行,他们的工作算是是第一个提出attention机制应用到NLP领域中。接着类似的基于attention机制的RNN模型扩展开始应用到各种NLP任务中。如何在CNN中使用attention机制也成为了大家的研究热点,近些年随着Transformer的火热,最新的文献越来越多的利用到了attention机制,如同Transformer论文标题一样,Attention is all you need。下图表示了attention研究进展的大概趋势。
二、Self Attention
前面也介绍Attention机制的大致发展,那什么是Self Attention呢,现考虑一个词性分析的问题(每个词对应一个词性,如动词、名词等),如果单独对每个词给一个FC网络,那对于句子I saw a saw中第一个saw和第二个saw很难区分出不同的类型,一个改进方向是可以采用窗口去包括更多词汇(RNN),但滑动窗口的大小不太好定,所以引入自注意力,直接考虑所有词汇。所以Self Attention是考虑了所有输入向量的信息,其作用相当于权重的重新分配(输入向量越相关其对应的权重越大),输出向量数量和输入向量数量保持一致。
接下来参考台大李宏毅自注意力机制对Self Attention进行一个简单的梳理(建议去看看原视频,讲解是真滴详细)。
2.1 向量之间相关性如何确定
如下图所示,假设输入是,对应的输出是,那么就需要确定和其他输入向量之间的相关性系数,
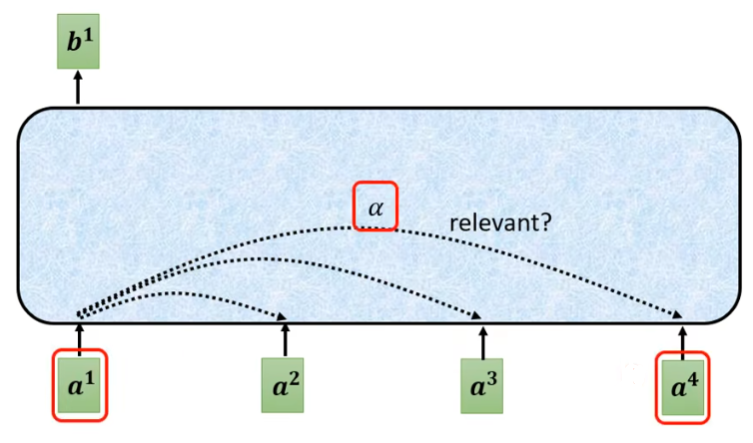
这个系数确定的方法有很多,常见的有Dot-Product和Additive两种方式,两者的基本组成如下图所示,后续都是采用Dot-product来进行。
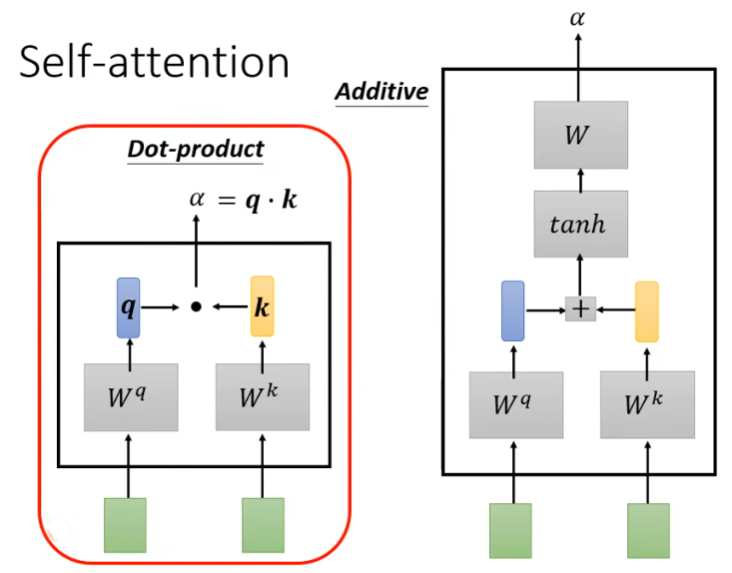
2.2 具体计算过程
这里演示如何通过Dot-Product计算系数,输入和矩阵相乘后得到作为query向量,然后分别与矩阵相乘后得到作为key向量,然后通过向量之间的点乘可以获得与得到作为输入向量和其他向量之间的相关系数,叫做:attention scores。
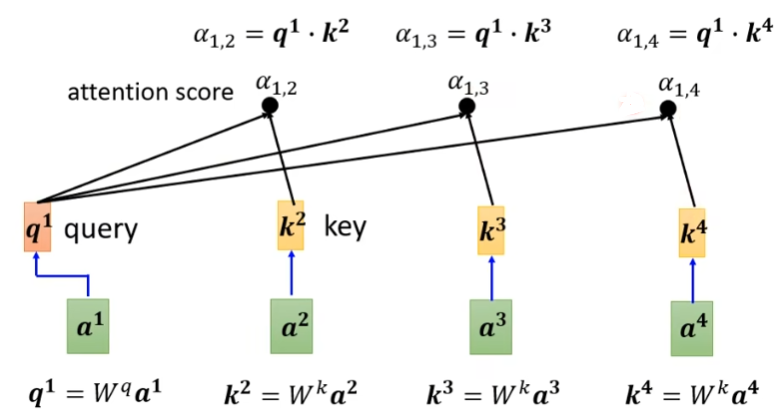
然后再采用Softmax函数对系数进行归一化处理,得到作为最终的系数。

输入分别与矩阵相乘后得到作为value向量,这些value向量与前面得到的系数相乘后求和即可得到对应的输出向量。
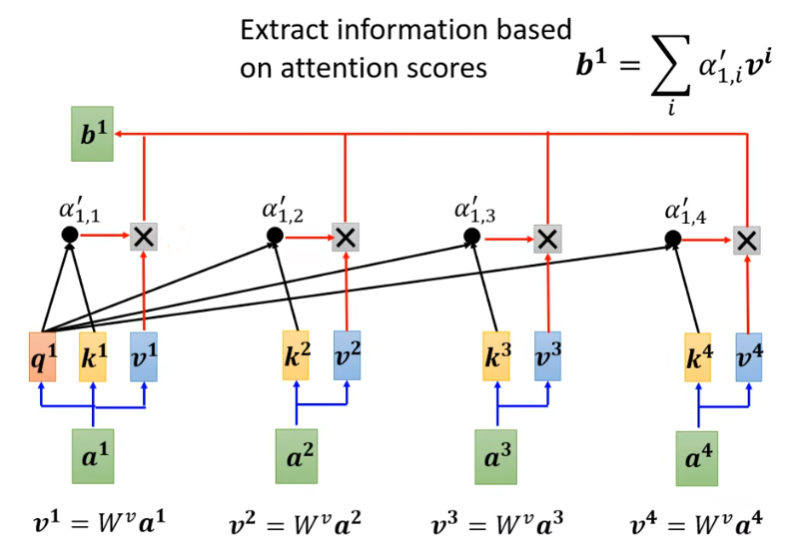
2.3 矩阵表示
以上过程通过矩阵表示如下图所示,输入通过矩阵相乘后分别得到,然后和Q相乘后得到所有的相关系数矩阵,最后和相乘得到输出。

整个过程里面对应的矩阵是需要学习的参数。
2.4 单头注意力与多头注意力
前面提到的就是单头注意力,对于多头注意力而言,类似于加多通道,可以经过矩阵生成,作为一组执行上述计算过程,然后又作为一组执行,依次类推,有多少个头就有多少组,下图演示两个头的例子,最后再把各个头的输出向量组合再一起作为最终的输出。如:加权组合后可以得到。
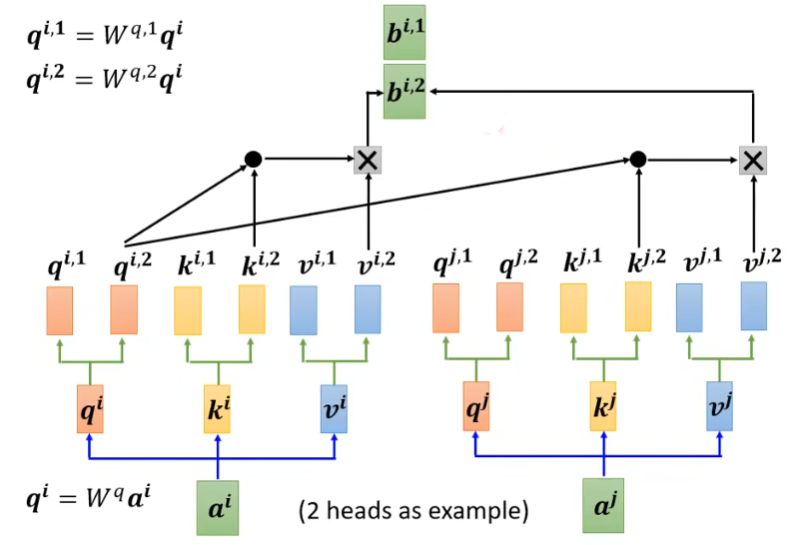
三、实现及动图展示
这个参考towardsdatascience,里面以动图的方式清晰的演示了整个过程,并且有对应的脚本实现。

Code
实现上总共分为以下7个步骤
# Step 1: Prepare inputs
import torch
x = [[1, 0, 1, 0], # Input 1
[0, 2, 0, 2], # Input 2
[1, 1, 1, 1], # Input 3
]
x = torch.tensor(x, dtype=torch.float32)
# Step 2: Initialise weights
w_key = [[0, 0, 1],
[1, 1, 0],
[0, 1, 0],
[1, 1, 0],
]
w_query = [[1, 0, 1],
[1, 0, 0],
[0, 0, 1],
[0, 1, 1],
]
w_value = [[0, 2, 0],
[0, 3, 0],
[1, 0, 3],
[1, 1, 0],
]
w_key = torch.tensor(w_key, dtype=torch.float32)
w_query = torch.tensor(w_query, dtype=torch.float32)
w_value = torch.tensor(w_value, dtype=torch.float32)
# Step 3: Derive key, query and value
keys = x @ w_key
querys = x @ w_query
values = x @ w_value
"""
>>> keys
tensor([[0., 1., 1.],
[4., 4., 0.],
[2., 3., 1.]])
>>> querys
tensor([[1., 0., 2.],
[2., 2., 2.],
[2., 1., 3.]])
>>> values
tensor([[1., 2., 3.],
[2., 8., 0.],
[2., 6., 3.]])
"""
# Step 4: Calculate attention scores
attn_scores = querys @ keys.T
"""
>>> attn_scores
tensor([[ 2., 4., 4.], # attention scores from Query 1
[ 4., 16., 12.], # attention scores from Query 2
[ 4., 12., 10.]]) # attention scores from Query 3
"""
# Step 5: Calculate softmax
from torch.nn.functional import softmax
attn_scores_softmax = softmax(attn_scores, dim=-1)
"""
>>> attn_scores_softmax
tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],
[6.0337e-06, 9.8201e-01, 1.7986e-02],
[2.9539e-04, 8.8054e-01, 1.1917e-01]])
"""
# For readability, approximate the above as follows
attn_scores_softmax = [[0.0, 0.5, 0.5],
[0.0, 1.0, 0.0],
[0.0, 0.9, 0.1]]
attn_scores_softmax = torch.tensor(attn_scores_softmax)
# Step 6: Multiply scores with values
weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None]
"""
>>> weighted_values
tensor([[[0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000]],
[[1.0000, 4.0000, 0.0000],
[2.0000, 8.0000, 0.0000],
[1.8000, 7.2000, 0.0000]],
[[1.0000, 3.0000, 1.5000],
[0.0000, 0.0000, 0.0000],
[0.2000, 0.6000, 0.3000]]])
"""
# Step 7: Sum weighted values
outputs = weighted_values.sum(dim=0)
"""
>>> outputs
tensor([[2.0000, 7.0000, 1.5000], # Output 1
[2.0000, 8.0000, 0.0000], # Output 2
[2.0000, 7.8000, 0.3000]]) # Output 3
"""
四、与CNN、RNN对比及其发展
Self attention v.s. CNN
参考论文《On the Relationship between Self-Attention and Convolutional Layers》
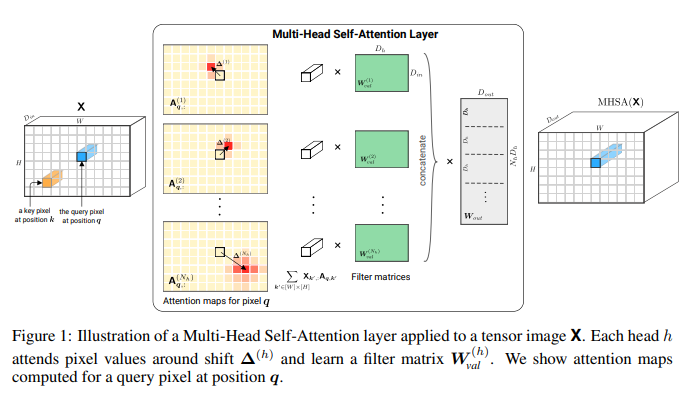
里面详细阐明了CNN是Self attention的一种特例,只要设定合适的参数Self attention就可以做到CNN一样的效果。
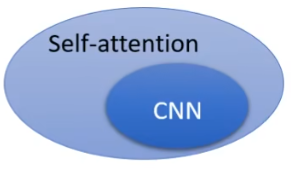
也可以从图片特征图上来看,self-attention关注整张特征图,而CNN是关注局部区域,所以CNN也可以理解成一个简化版的self-attention。
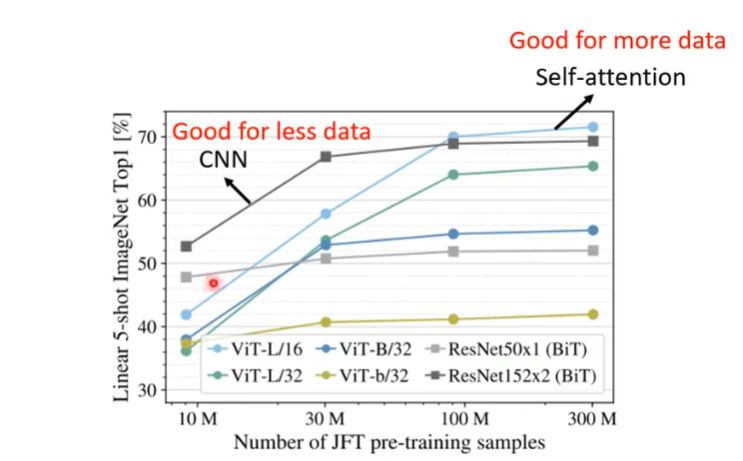
另外还可以参考一下论文VIT,通过将图片划分成16 * 16的小块,进而将Transformer从NLP领域转到CV领域,其通过实验发现CNN在数据量少的时候效果比较好,而Self-attention在数据量大的情况下效果更好。
Self Attention v.s. RNN
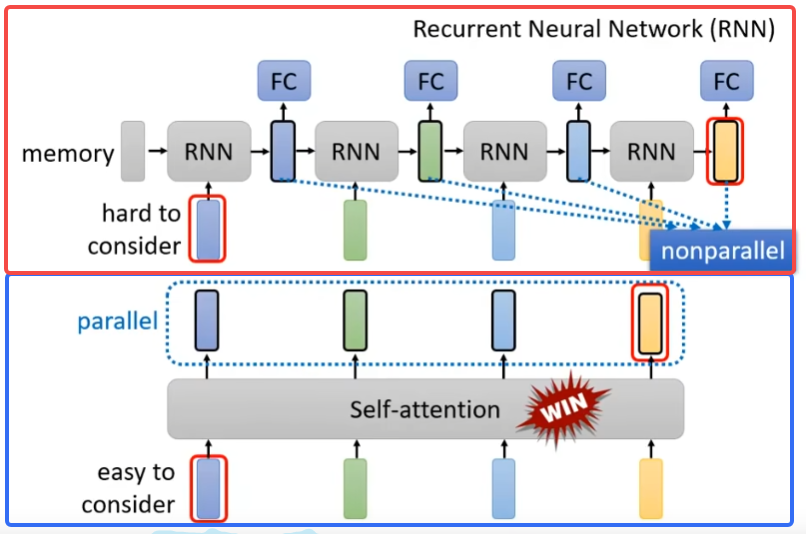
RNN最大的特点就是后续的预测依赖于前面的输出,这也就导致RNN无法并行,而且由于长度的限制,RNN很难关连到很久之前的信息,而Self attention则避开了这些缺陷。
如下图所示,红色框表示RNN,蓝色框表示Self-attention
另外感兴趣的还可以参考《Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention》,可以看到Self-Attention加上一些东西后就可以转变为RNN。
Self Attention v.s. 全连接网络
如果全连接网络前后节点数量一致,在形式上两者有点相似,但是全连接网络学习的是从一个特征空间到另一个特征空间,其关注的是当前节点的重要性,而自注意力学习的是当前特征空间不同节点之间的关系,和位置无关。也就是对于自注意力机制 ABC和CAB得到的特征相同,而全连接ABC和CAB由于位置变化其最终特征是不一样的。
参考:https://www.zhihu.com/question/320174043
Self Attention变形及发展
变形的主要目是减少运算量,追求速度和精度的平衡。重点可以查看以下两篇文献。
《Long Range Arena: A Benchmark for Efficient Transformers》
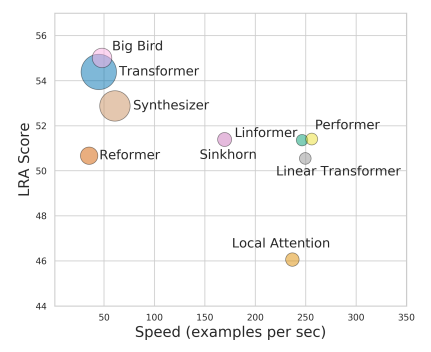
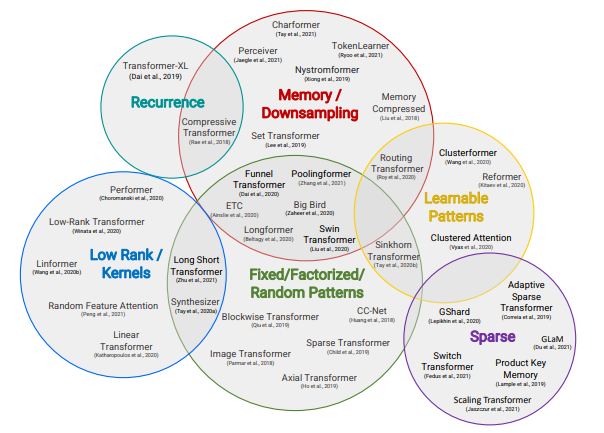
《Efficient Transformers: A Survey》





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署