判断射线和AABB（Axis-Aligned Bounding Box）是否相交

已知条件

$ori(x, y, z)$表示射线起点坐标

$dir(x, y, z)$表示射线方向(单位向量)

$Bound$表示AABB包围盒

$Bound.MinBound$表示包围盒在各轴向最小坐标

$Bound.MaxBound$表示包围盒在各轴向最大坐标

一般平面方程为$aX+bY+cZ+d=0$，因为AABB的六个面分别平行于$XY$、$XZ$、$YZ$平面，所以平面的方程为$X=d$，$Y=d$，$Z=d$

射线与平面的交点可表示为：$P = ori + t * dir$，$t$为射线起点到平面的斜向距离

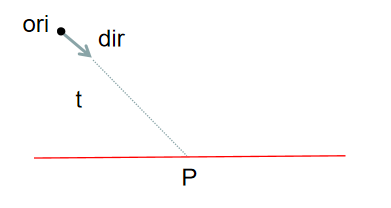
一、方法一： 依次判断和近面是否相交

如果射线和AABB相交，则射线必定先和三个近面中的一个相交，所以依次判断是否相交即可

步骤

• 判断起点是否在内部，如果在内部则必相交，否则
• 遍历每个轴向，求出和近面的交点
• 判断交点是否在包围盒内部

脚本

// dir为单位向量
bool IntersectRayAndAABB(const Bound& bound, const Point3& ori, const Point3& dir) 
{
    Point3 minBound = bound.GetMinBound(), maxBound = bound.GetMaxBound();
    // 首先判断是否在内部，内部一定相交
    if(ori.x > minBound.x && ori.x < maxBound.x &&
       ori.y > minBound.y && ori.y < maxBound.y &&
       ori.z > minBound.z && ori.z < maxBound.z)
    {
        return true;
    }
    // 分别判断射线和各轴近面的相交情况 
    for (int axis = 0; axis < 3; axis++) {
        double t = 0.0;
        if(std::abs(dir[axis]) > std::numeric_limits<double>::epsilon()){
            if(dir[axis] > 0){
                t = (minBound[axis] - origin[axis]) / dir[axis];
            }
            else{
                t = (maxBound[axis] - origin[axis]) / dir[axis];
            }
        }
        if(t > 0){   // 射线和平面相交
            // 判断交点是否在面内
            const Point3 pt = ori + t * dir;
            if(minBound[(axis + 1) % 3] < pt[(axis + 1) % 3] && pt[(axis + 1) % 3] < maxBound[(axis + 1) % 3] && 
               minBound[(axis + 2) % 3] < pt[(axis + 2) % 3] && pt[(axis + 2) % 3] < maxBound[(axis + 2) % 3])
            {
                return true
            }
        }
    }
	
    return false;
	
} 

二、方法二：slabs

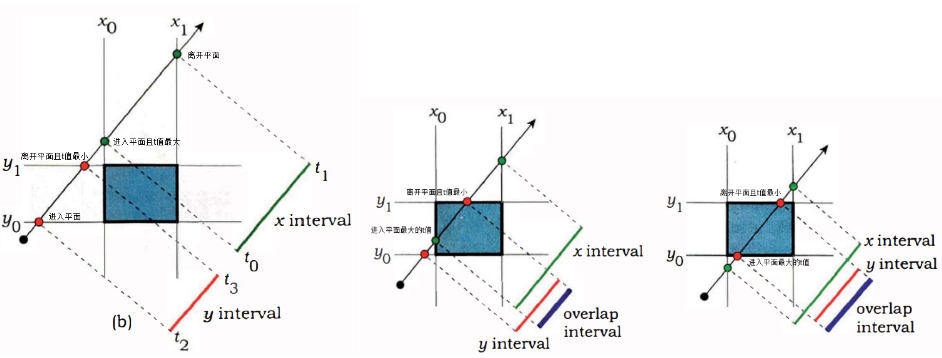
观察上图可知，光线与平面相交时$t$的区间会交叠，即当光线进入平面处的最大$t$值小于光线离开平面处的最小$t$值时射线和AABB会相交。

步骤

• 遍历每个轴向，记录$tMin$和$tMax$
• 对比$tMin$和$tMax$

脚本

bool IntersectRayAndAABB(const Bound& bound, const Point3& ori, const Point3& dir) 
{ 
     double tMin = 0;    // tMin设为0，可以有效过滤掉内部情况
     double tMax = std::numeric_limits<double>::max();
     Point3 minBound = bound.GetMinBound(), maxBound = bound.GetMaxBound();
     for (int axis = 0; axis < 3; axis++) {
	 if (std::abs(dir[axis]) < std::numeric_limits<double>::epsilon()) {  // 射线方向与某个轴向平行
             if (ori[axis] > maxBound[axis] || ori[axis] < minBound[axis]){  // 起点同时在Bound于该轴的两侧，则不相交
                 return false;  
             }
             continue;
         }
	 double invD = 1 / dir[axis];
	 double tNear = invD * (minBound[axis] - ori[axis]);  // 计算射线起点到平面的斜向距离
	 double tFar = invD * (maxBound[axis] - ori[axis]);
	 if (tNear > tFar) {
             std::swap(tNear, tFar);
         }
	 if (tNear > tMin) {
             tMin = tNear;
         }
	 if (tFar < tMax) {
             tMax = tFar;
         }
	 if (tMin > tMax) {
             return false;
         }
     }
     return true;
}

参考链接

https://blog.csdn.net/u012325397/article/details/50807880