射线和三角面求交

一、平面射线与线段是否相交

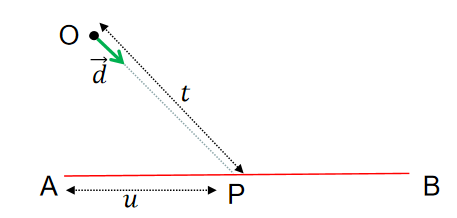
1.1 相交检测

步骤

1、判断射线方向\(\vec{d}\)（单位向量）是否与线段所在方向\(\vec{AB}\)是否平行，如果平行则不相交

2、假设射线与线段交点为\(P\)，则计算\(|\vec{AP}|\)与\(|\vec{AB}|\)的比例\(u\)

3、如果\(u < 0\)或者\(u > 1\)则不相交

4、计算出\(|\vec{OP}|\)的长度 \(t\)，由\(P = O + t * \vec{d}\)即可计算出交点坐标

关键过程

1、\(\vec{d}\)是否与\(\vec{AB}\)平行

判断\(\vec{d}\)是否和\(\vec{AB}\)平行可以采用向量叉乘，如果叉乘结果为零，则表示两向量平行

2、计算\(u\)和\(t\)

设交点为\(P\)，其坐标可以表示为：

\(P = O + t * \vec{d} = A + u * \vec{AB}\)

所以：

\(u * \vec{AB} - t * \vec{d} = \vec{AO}\)

即有：

\[\left\{\begin{matrix} ux_{AB} - tx_d = x_{AO} \\ uy_{AB} - ty_d = y_{AO} \end{matrix}\right.\]

依据克莱姆法则可知：

\[u = \frac{D_1}{D} \]

\[t = \frac{D_2}{D} \]

其中：

\[D = \begin{vmatrix} x_{AB} & -x_d\\ y_{AB} & -y_d\\ \end{vmatrix}\]

\[D_1 = \begin{vmatrix} x_{AO} & -x_d\\ y_{AO} & -y_d\\ \end{vmatrix}\]

\[D_2 = \begin{vmatrix} x_{AB} & x_{AO}\\ y_{AB} & y_{AO}\\ \end{vmatrix}\]

1.2 几何意义

如下图向量\(\vec{AB}\)与\(\vec{AO}\)构成成平行四边形\(ABB'O\)，向量\(\vec{OP}\)与\(\vec{A'B'}\)构成平行四边形\(OPP’B'\)（\(\vec{A'B'}\)为\(\vec{AB}\)平移到\(A\)与\(O\)重合），由于底边长都是\(|\vec{AB}|\)且高度相同，所以这两个平行四边形面积相等。

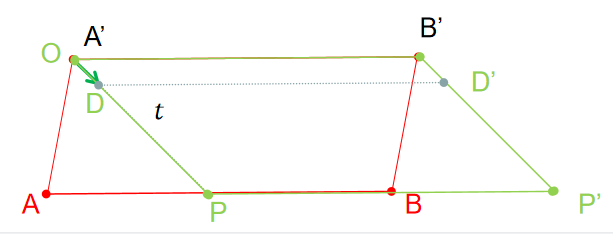
另外平面向量叉乘可以表示两向量组成平行四边形的有向面积，所以\(t\)可以表示为\(\vec{AB}\)与\(\vec{AO}\)的叉乘除以\(\vec{AB}\)与单位方向向量\(\vec{d}\)的叉乘，即上面的\(t = \frac{D_2}{D}\)中\(D\)在该例中表示\(S_{ODD'B'}\)，\(D_2\)表示\(S_{ABB'O}\)。

1.3 代码实现

bool RayIntersection(const Point2 & ori, const Vector2& dir, const Point2& A, const Point2& B, double& t)
{
    Vector2 AB = B - A;
    // 1. 判断是否平行
    if (std::abs(dir.Cross(AB)) < std::numeric_limits<double>::epsilon() ){
        return false;
    }
    dir.Normalize();  // 归一化向量
    
    Vector2 AO = ori - A;
    
    double D = AB.Cross(-dir);
    double D1 = AO.Cross(-dir);  
     
    if(D1 < 0 || D1 > D){         // 减少一次除法运算,即 0 <= u <= 1。超出线段AB范围
        return false;
    }
    
    double D2 = AB.Cross(AO);
    t = D2 / D;
    return true;
}

二、空间射线与三角面是否相交

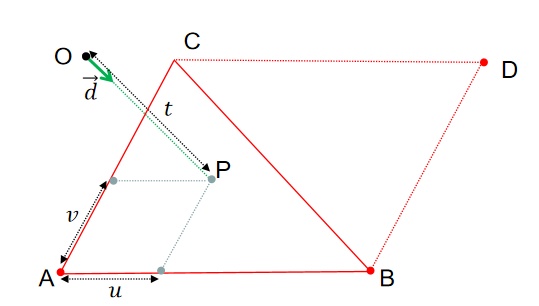
2.1 相交检测

步骤

1、判断射线方向\(\vec{d}\)（单位向量）与三角面所在平面是否共面，如果不共面则进行后续步骤，否则需要退回二维情况进行判断

2、假设射线与三角面\(ABC\)交点为\(P\)，则计算\(\vec{AP}\)在向量\(\vec{AB}\)方向的比例\(u\)和在向量\(\vec{AC}\)方向的比例\(v\)

3、如果\(u < 0\)或者\(u > 1\)则不相交

4、如果\(v < 0\)或者\(u + v > 1\)则不相交（如果\(u+v>1\)，则交点落在三角面\(BCD\)内）

4、计算出\(|\vec{OP}|\)的长度 \(t\)，由\(P = O + t * \vec{d}\)即可计算出交点坐标

关键过程

1、\(\vec{d}\)是否与面\(ABC\)共面

可以采用\(\vec{AB}\)和\(\vec{AC}\)的向量叉乘计算出法线\(\vec{n}\)，法线\(\vec{n}\)满足右手法则，其长度表示平行四边行\(ABDC\)的面积；

然后判断法线\(\vec{n}\)和方向向量\(\vec{d}\)的点乘是否为零，点乘为零则表示共面

2、计算\(u\)，\(v\)和\(t\)

设交点为\(P\)，其坐标可以表示为：

\(P = O + t * \vec{d} = A + u * \vec{AB} + v * \vec{AC}\)

所以：

\(u * \vec{AB} + v*\vec{AC}- t * \vec{d} = \vec{AO}\)

即有：

\[\left\{\begin{matrix} ux_{AB} + vx_{AC}- tx_d = x_{AO} \\ uy_{AB} + vy_{AC}- ty_d = y_{AO} \\ uz_{AB} + vz_{AC}- tz_d = z_{AO} \end{matrix}\right.\]

依据克莱姆法则可知：

\[u = \frac{D_1}{D} \]

\[v = \frac{D_2}{D} \]

\[t = \frac{D_3}{D} \]

其中：

\[D = \begin{vmatrix} x_{AB} & x_{AC} & -x_d\\ y_{AB} & y_{AC} & -y_d\\ z_{AB} & z_{AC} & -z_d\\ \end{vmatrix}\]

\[D_1 = \begin{vmatrix} x_{AO} & x_{AC} & -x_d\\ y_{AO} & y_{AC} & -y_d\\ z_{AO} & z_{AC} & -z_d \\ \end{vmatrix}\]

\[D_2 = \begin{vmatrix} x_{AB} & x_{AO} & -x_{d}\\ y_{AB} & y_{AO} & -y_{d}\\ z_{AB} & z_{AO} & -z_{d}\\ \end{vmatrix}\]

\[D_3 = \begin{vmatrix} x_{AB} & x_{AC} & x_{AO}\\ y_{AB} & y_{AC} & y_{AO}\\ z_{AB} & z_{AC} & z_{AO}\\ \end{vmatrix}\]

2.2 几何意义

如下图向量\(\vec{AB}\)与\(\vec{AC}\)以及\(\vec{AO}\)构成成平行六面体（红色），向量\(\vec{A'O}\)与\(\vec{A'B'}\)以及\(\vec{A'C'}\)构成平行六面体（绿色）（\(\vec{A'B'}\)为\(\vec{AB}\)平移到\(A\)与\(P\)重合，\(\vec{A'C'}\)为\(\vec{AC}\)平移到\(A\)与\(P\)重合），由于底面都是\(ABDC\)且高度相同，所以这两个平行六面体体积相等。

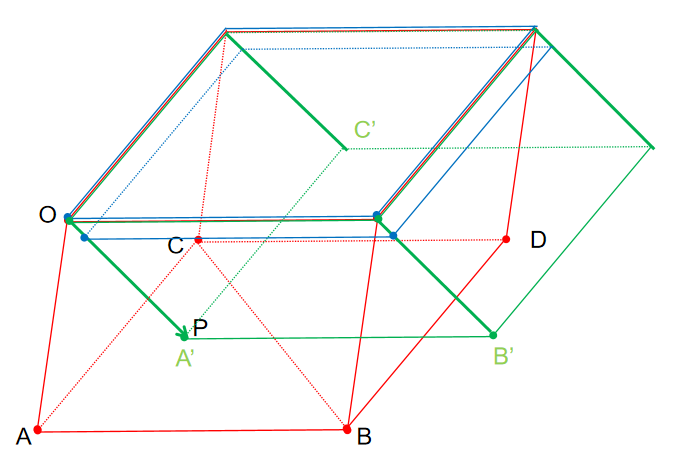
另外三维向量叉乘可以结果长度表示两向量组成平行四边形的面积，方向为两个组成平面的法线方向，三个三维向量的混合积（先叉乘（底面积）再点乘（高））表示其有向体积。所以\(t\)可以表示为\(\vec{AB}\)与\(\vec{AC}\)以及\(\vec{AO}\)的混合积除以单位方向\(\vec{AB}\)与\(\vec{AC}\)以及向量\(\vec{d}\)的混合积，即上面的\(t = \frac{D_3}{D}\)中\(D\)在该例中表示蓝色平行六面体的有向体积，\(D_3\)表示红色平行六面体有向体积。

2.3 代码实现

bool RayIntersection(const Point3 & ori, const Vector3& dir, const Point3& A, const Point3& B, double& t)
{
    Vector3 AB = B - A;
    Vector3 AC = C - A;
    
    Vector3 n = AB.Cross(AC);
    // 1. 判断是否共面
    if (std::abs(dir.Dot(n)) < std::numeric_limits<double>::epsilon() ){
        // 共面，需要转换到平面判断是否相交，这里直接认为不相交
        return false;
    }
    dir.Normalize();  // 归一化向量
    
    Vector3 AO = ori - A;
    
    double D = n.Dot(-dir);
    double D1 = AO.Cross(AC).Dot(-dir);  
     
    if(D1 < 0 || D1 > D){         // 减少一次除法运算,即 0 <= u <= 1。超出线段AB范围
        return false;
    }
    
    double D2 = AB.Cross(AO).Dot(-dir);
    // 减少一次除法运算，即0 <= v <= 1, 其他情况超出线段AC的范围， 这里u+v<1限制落在三角面ABC中，u+v>1可能会落在BCD或四边形ABDC外部
    if(D2 < 0 || D1 + D2 > D){   
        return false;
    }
    
    double D3 = n.Dot(AO)
    t = D3 / D;
    return true;
}