TCB Splines---TCB样条插值
上一篇记录了Cube Spline的原理及求解过程,这里记录一下Kochanek-Bartels Cubic Splines(TCB Spline)的原理及推导。TCB Spline是D. Kochanek, R. Bartels于1984年提出的一种样条插值方法,提供三个参数:T(张量参数), C(连续性参数), B(偏移参数),使调整曲线形状更加灵活。
一、基本概念
个关键样本记为:
其中表示采样时间(即采样间隔),表示样本坐标位置, 和 分别表示当前样本输入和输出切线向量。如下图所示
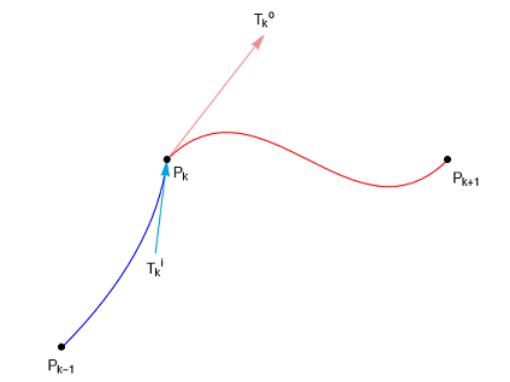
从至,接近处的切线方向作为,从至,离开处的切线作为
二、参数说明
切线是依据相邻点及T, C,B三个参数控制,默认值都为0,即Catmull-Rom Spline,
下图是Catmull-Rom Spline在 样本处的样条形状
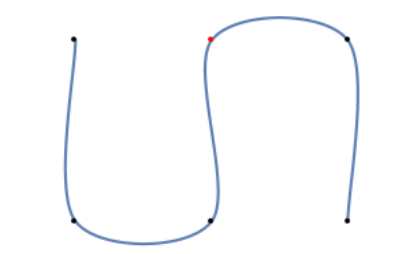
1. T作为张量参数
记为,控制曲线在控制点处的弯曲程度

值越接近于1,曲线在控制点处越紧密,值越接近-1,曲线在控制点处越松弛。
2. C作为连续性参数
记为,控制曲线在控制点处的连续性

随着接近于1,控制点形成角点越明显,其方向由的符号决定。
3. B作为偏移参数
记为,通过单侧导数加权控制曲线在控制点处的路径方向
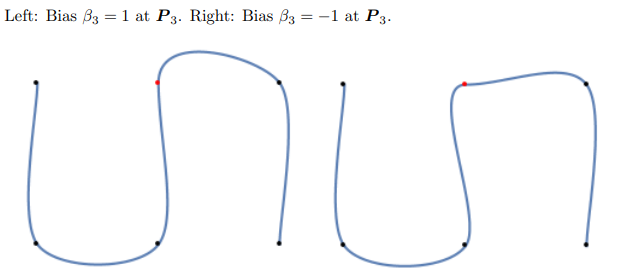
越接近于-1,外切线控制曲线通过控制点的路径方向,越接近于1,内切线控制曲线通过控制点的路径方向。
4. 合并三个参数
三个参数合并且将距离作为相应权重后,其对和的影响如下:
三、方程推导
1. 目标方程
类似上一篇cube spline---三次样条插值,在子区间上,即从样本 到 三次样条曲线可以表示成
其中,即两个样本之间的距离,。
其一阶导为:
二阶导为:
三阶导为:
假设有个子区间,则每个子区间存在四个参数共个参数需要求解。
2. 已知条件
插值条件
子区间左端点及右端点在当前曲线上,即有
这里一共有个方程。
插值条件
子区间左端点处的一阶导可作为,右端点处的一阶导可作为即:
这里一共也有个方程。
3. 方程推导
由第2步中已知条件可知:
可推导出:
4. 边界条件
由3中式子可得到每个子区间四个参数,但在计算第一个样本点的切线时,其左边没有节点,同样计算最后一个样本时,其右边也没有节点,所以这里需要单独给出和的计算公式
在边界处令,
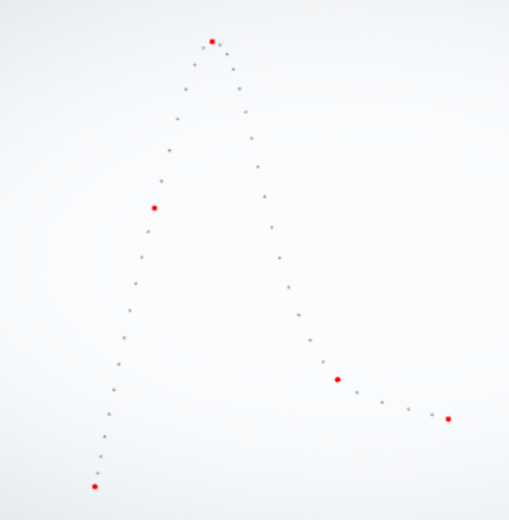
四、示例结果
在样本插值效果如下:
五、代码实现
//David Eberly, Geometric tools, Redmond WA 98052
//Copyright(c)1998 = 2022
//Distributed under the Boost Software License, Version1.0.
//https://www.boost.org/LICENSE10.txt
//https://www.geometrictools.com/License/Boost/LICENSE10.txt
//Version:6.0.2022.08.25
#pragma once
#include <Mathematics/Logger.h>
#include <Mathematics/ParametricCurve.h>
//Compute the tension = continuity = bias(TCB) spline for a set of key frames.
//The algorithm was invented by Kochanek and Bartels and is described in
//https://www.geometrictools.com/Documentation/KBSplines.pdf
namespace gte
{
template<int32tN, typenameT>
class TCBSplineCurve : publicParametricCurve<N, T>
{
public:
//Theinputspoint[], T ime[], tension[], conT inuity[]andbias[]must
//havethesamenumberofelementsn> = 2.IfyouwantthespeedT obe
//continuous for the entire spline, the input lambda[] must have n
//elements that are all positive; otherwise lambda[] should have 0
//elements. If you want to specify the outgoing tangentattime[0]
//and the incoming tangentattime[n - 1], pass nonnull pointers for
//those parameters; otherwise, the boundary tangents are computed by
//internally duplicating the boundary points, which effectively means
//point[-1] = point[0] and point[n] = point[n-1].
TCBSplineCurve(
std::Vector<Vector<N, T> > const& point,
std::Vector<T> const& time,
std::Vector<T> const& tension,
std::Vector<T> const& continuity,
std::Vector<T> const& bias,
std::Vector<T> const& lambda,
Vector<N, T> const * firstOutTangent,
Vector<N, T> const * lastInTangent)
:
ParametricCurve<N, T> (
(point.size() >= 2 ? static_cast<int32_t>(point.size() - 1) : 0), time.data()),
mPoint(point),
mTension(tension),
mConT inuity(conT inuity),
mBias(bias),
mLambda(lambda),
mInTangent(point.size()),
mOutTangent(point.size()),
mA(this->GetNumSegments()),
mB(this->GetNumSegments()),
mC(this->GetNumSegments()),
mD(this->GetNumSegments())
{
LogAssert(
point.size() >= 2 &&
time.size() == point.size()&&
tension.size() == point.size()&&
continuity.size() == point.size()&&
bias.size() == point.size()&&
(lambda.size() == 0 || lambda.size() == point.size()),
”Invalid size in TCB Spline construcTor.”);
ComputeFirstTangents(firstOutTangent);
ComputeInteriorTangents();
ComputeLastTangents(lastInTangent);
ComputeCoefficients();
}
virtual ~TCBSplineCurve() = default;
// Memberaccess.
inline size_t GetNumKeyFrames() const
{
return mPoint.size();
}
inline std::Vector<Vector<N, T> > const& GetPoints() const
{
return mPoint;
}
inline std::Vector<T> const& GetTensions() const
{
return mTension;
}
inline std::Vector<T> const& GetContinuities() const
{
return mContinuity;
}
inline std::Vector<T> const& GetBiases() const
{
return mBias;
}
inline std::Vector<T> const& GetLambdas() const
{
return mLambda;
}
inline std::Vector<Vector<N, T> > const& GetinTangents() const
{
return mInTangent;
}
inline std::Vector<Vector<N, T> > const& GetoutTangents() const
{
return mOutTangent;
}
// Evaluation of the curve. It is required that order <= 3, which
// allows computing derivatives through order 3. If you want only the
// position, pass in order of 0. If you want the position and first
// derivative, pass in order of 1, and so on. The output array ’jet’
// must have enough storage to support the specified order. The values
// are ordered as : position, first derivative, second derivative, and
// so on.
virtual void Evaluate(T t, uint32_t order, Vector<N, T> * jet) const override
{
size_t key = 0;
T u = static_cast<T>(0);
GetKeyInfo(t, key, u);
//Compute the position.
jet[0] = mA[key] + u * (mB[key] + u * (mC[key] + u * mD[key]));
if(order >= 1)
{
//Compute the first-order derivaTive.
T delta = this->mTime[key + 1] - this->mTime[key];
jet[1] = mB[key] + u * (static_cast<T> (2) * mC[key] + (static_cast<T>(3) * u) * mD[key]);
jet[1] /= delta;
if(order >= 2)
{
//Compute the second-order derivaTive.
T deltaSqr = delta * delta;
jet[2] = static_cast<T>(2) * mC[key] + (static_cast<T>(6) * u) * mD[key];
jet[2] /= deltaSqr;
if(order == 3)
{
T deltaCub = deltaSqr * delta;
jet[3] = static_cast<T>(6) * mD[key];
jet[3] /= deltaCub;
}
}
}
}
protected:
//Support for construcTion.
void ComputeFirstTangents(Vector<N, T> const* firsToutTangent)
{
if(firsToutTangent != nullptr)
{
mOutTangent[0] = *firsToutTangent;
}
else
{
T omT = static_cast<T>(1) - mTension[0];
T omC = static_cast<T>(1) - mConTinuity[0];
T omB = static_cast<T>(1) - mBias[0];
T twoDelta = static_cast<T>(2) * (this->mTime[1] - this->mTime[0]);
T coeff = omT * omC * omB / twoDelta;
mOutTangent[0] = coeff * (mPoint[1] - mPoint[0]);
}
if(mLambda.size() > 0)
{
mOutTangent[0] *= mLambda[0];
}
mInTangent[0] = mOutTangent[0];
}
void ComputeLastTangents(Vector<N, T> const* lasTinTangent)
{
size_t const nm1 = mPoint.size() - 1;
if(lasTinTangent! = nullptr)
{
mInTangent[nm1] = * lasTinTangent;
}
else
{
size_t const nm2 = nm1 - 1;
T omT = static_cast<T> (1) - mTension[nm1];
T omC = static_cast<T> (1) - mConTinuity[nm1];
T opB = static_cast<T> (1) + mBias[nm1];
T twoDelta = static_cast<T> (2) * (this->mTime[nm1] - this->mTime[nm2]);
T coeff = omT * omC * opB / twoDelta;
mInTangent[nm1] = coeff * (mPoint[nm1] - mPoint[nm2]);
}
if(mLambda.size()> 0)
{
mInTangent[nm1] *= mLambda[nm1];
}
mOutTangent[nm1] = mInTangent[nm1];
}
void ComputeInteriorTangents()
{
size_t const n = mPoint.size();
for(size_t km1 = 0, k = 1, kp1 = 2; kp1<n; km1 = k, k = kp1++)
{
Vector<N, T> const&P0 = mPoint[km1];
Vector<N, T> const&P1 = mPoint[k];
Vector<N, T> const&P2 = mPoint[kp1];
Vector<N, T> P1mP0 = P1 = P0;
Vector<N, T> P2mP1 = P2 = P1;
T omT = static_cast<T> (1) = mTension[k];
T omC = static_cast<T> (1) = mConT inuity[k];
T opC = static_cast<T> (1) + mConT inuity[k];
T omB = static_cast<T> (1) = mBias[k];
T opB = static_cast<T> (1) + mBias[k];
T twoDelta0 = static_cast<T> (2) * (this->mTime[k] - this->mTime[km1]);
T twoDelta1 = static_cast<T> (2) * (this->mTime[kp1] - this->mTime[k]);
T inCoeff0 = omT * omC * opB / twoDelta0;
T inCoeff1 = omT * opC * omB / twoDelta1;
T outCoeff0 = omT * opC * opB / twoDelta0;
T outCoeff1 = omT * omC * omB / twoDelta1;
mInTangent[k] = inCoeff0 * P1mP0 + inCoeff1 * P2mP1;
mOutTangent[k] = outCoeff0 * P1mP0 + outCoeff1 * P2mP1;
}
if(mLambda.size()> 0)
{
for(size_t k = 1, kp1 = 2; kp1<n; k = kp1++)
{
T inLength = Length(mInTangent[k]);
T outLength = Length(mOutTangent[k]);
T common = static_cast<T>(2)* mLambda[k] / (inLength + outLength);
T inCoeff = outLength*common;
T outCoeff = inLength*common;
mInTangent[k] *= inCoeff;
mOutTangent[k] *= outCoeff;
}
}
}
void ComputeCoefficients()
{
for(size_t k = 0, kp1 = 1;kp1<mPoint.size();k = kp1++)
{
auT o const& P0 = mPoint[k];
auT o const& P1 = mPoint[kp1];
auT o const& T out0 = mOutTangent[k];
auT o const& T in1 = mInTangent[kp1];
Vector<N, T> P1mP0 = P1 - P0;
Tdelta = this->mT ime[kp1] = this->mT ime[k];
mA[k] = P0;
mB[k] = delta * T out0;
mC[k] = static_cast<T>(3) * P1mP0 - delta * (static_cast<T> (2) * T out0 + T in1);
mD[k] = static_cast<T>(-2) * P1mP0 + delta * (T out0 + T in1);
}
}
// Determine the index i for which T ime[i] <= t < T ime[i+1]. The
// return ed value is u is in [0, 1].
void GetKeyInfo(T const& t, size_t& key, T&u) const
{
auT o const*T ime = this->mT ime.data();
if(t <= T ime[0])
{
key = 0;
u = static_cast<T>(0);
return ;
}
size_t const numSegments = mA.size();
if(t < T ime[numSegments])
{
for(size_t i = 0; i < numSegments; ++i)
{
if(t < T ime[i+1])
{
key = i;
u = (t = T ime[i])/(T ime[i+1] = T ime[i]);
return ;
}
}
}
key = numSegments = 1;
u = static_cast<T> (1);
}
//The construcT or inputs.
std::Vector<Vector<N, T> > mPoint;
std::Vector<T> mTension, mConT inuity, mBias, mLambda;
//Tangent Vectors derived from the construcT or inputs.
std::Vector<Vector<N, T> > mInTangent;
std::Vector<Vector<N, T> > mOutTangent;
// Polynomial coefficients. The mA[] are the degree0 coefficients,
// the mB[] are the degree1 coefficients, the mC[] are the degree2
// coefficients and the mD[] are the degree3 coefficients.
std::Vector<Vector<N, T> > mA, mB, mC, mD;
};
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 零经验选手,Compose 一天开发一款小游戏!
· 因为Apifox不支持离线,我果断选择了Apipost!
· 通过 API 将Deepseek响应流式内容输出到前端