线段相交
记两线段为与
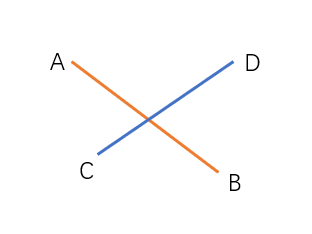
一、方法一
1. 先判断线段是否共线
依据共线向量叉乘为零来判断
与叉乘是否为0,如果为0则共线
2. 在不共线情况下判断是否相交
依据且来判断,其中和的推导过程如下:
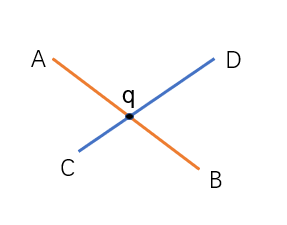
假设交点为,则有且
即
由于向量自身的叉乘为0,所以上式两边同时叉乘可得:
,
变形可得:
同理,两边同时叉乘可得:,所以:
3. 在相交的情况下计算交点
依据第2步计算的和,代入:且 即可求出交点的坐标
代码实现
struct Point {
float x, y;
Point(const float& px = 0, const float& py = 0) : x(px), y(py) {}
Point operator+(const Point& p) const {
return Point(x + p.x, y + p.y);
}
Point& operator+=(const Point& p) {
x += p.x;
y += p.y;
return *this;
}
Point operator-(const Point& p) const {
return Point(x - p.x, y - p.y);
}
Point operator*(const float coeff) const {
return Point(x * coeff, y * coeff);
}
};
float Dot2d(const Point & A, const Point & B) {
return A.x * B.x + A.y * B.y;
}
float Cross2d(const Point & A, const Point & B) {
return A.x * B.y - B.x * A.y;
}
bool IsInsert(const Point& A, const Point& B, const Point& C, const Point&D)
{
Point AB = B - A;
Point CD = D - C;
float det = Cross2d(CD , AB);
// This takes care of parallel lines
if (std::fabs(det) <= 1e-14) {
return false;
}
Point AC= C - A;
double t = Cross2d(CD, AC) / det;
double u = Cross2d(AB, AC) / det;
if (t > -EPS && t < 1.0f + EPS && u > -EPS && u < 1.0f + EPS) {
return true;
// intersections P = A + AB * t;
}
}
二、方法二
1. 先判断线段是否共线
同方法一
2. 在不共线情况下判断是否相交
依据线段相交则一条线段两端点位于另一线段两侧来判断
相交情况下有如下两种情形:
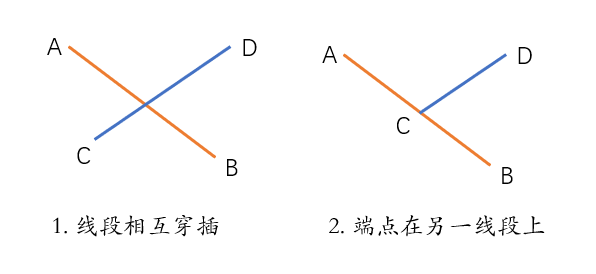
判断是否在两侧可以依据两个向量的叉乘(右手法则),如下:
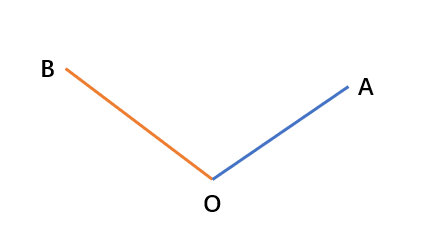
,则在的逆时针方向
,则在的顺时针方向
所以在相交的两种情况下有:
- 情况1
点和在两侧,则有:
点和在两侧,则有:
- 情况2
由于端点在线段上,所以有一个叉乘为0,因此:
且
代码实现
bool IsInsert(const Point& A, const Point& B, const Point& C, const Point&D)
{
Point AB = B - A;
Point CD = D - C;
Point AC = C - A;
Point AD = D - A;
Point CB = B - C;
Point CA = -AC;
float det = Cross2d(CD , AB);
// This takes care of parallel lines
if (std::fabs(det) <= 1e-14) {
return false;
}
if (Cross2D(AC, AB) * Cross2D(AD, AB) <= EPS && Cross2D(CA, CD) * Cross2D(CB, CD)< EPS) {
return true;
}
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 零经验选手,Compose 一天开发一款小游戏!
· 因为Apifox不支持离线,我果断选择了Apipost!
· 通过 API 将Deepseek响应流式内容输出到前端