矩方法应用

  最近用到了矩方法对目标检测的结果进行后处理，包括求中心点，偏角和长短轴。基本步骤如下：

• 第一步：将检测到物体的平行框位置作为ROI区域；
• 第二步：对ROI区域进行预处理（灰度化、二值化）；
• 第三步：利用矩方法求出物体的矩（OPENCV::moments）；
• 第四步：利用矩分别计算中心点，偏角和长短轴。

理论部分可以参考这篇博客。

一、求中心点

单通道图像的矩的面积为：
$$M_{00} = \sum_{i} \sum_{j}V(i, j)$$
其中$V(i, j)$表示单通道图像在点$(i, j)$上的灰度值，一阶矩定义为：
$$M_{10}=\sum_{i}\sum_ {j}i\cdot V(i,j)$$
$$M_{01}=\sum_{i}\sum_ {j}j\cdot V(i,j)$$
通过一阶矩求出物体重心位置：
$$x_c = \frac{M_{10}}{M_{00}}$$
$$y_c = \frac{M_{01}}{M_{00}}$$

二、求偏角

物体的二阶矩定义为：

$$M_{20} = \sum_{i} \sum_{j} i^2 \cdot V(i,j)$$

$$M_{02} = \sum_{i} \sum_{j} j^2 \cdot V(i,j)$$

$$M_{11} = \sum_{i} \sum_{j} i\cdot j \cdot V(i,j)$$

通过二阶矩计算偏转角度：

$$\theta = \frac{1}{2}atan2 \frac{2b}{a-c}$$

其中$a = \frac{M_{20}}{M_{00}}-{x_c}^2$,$b = \frac{M_{11}}{M_{00}}-x_c\cdot y_c$,$c = \frac{M_{11}}{M_{00}}-{y_c}^2$。
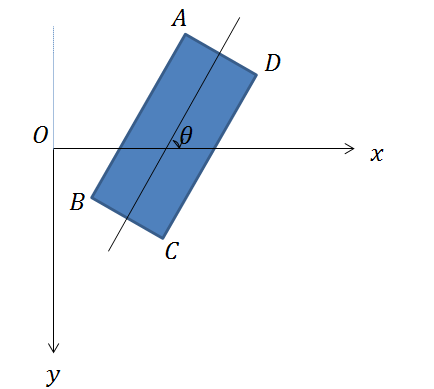
求出的角度为$x$轴正方向与物体长轴所形成的角度，其范围为$[-90^o, 90^o]$，$x$轴正向的逆时针方向为负，顺时针为正。

三、求长短轴

长半轴$r_1$和短半轴$r_2$定义为：

$$r_1 = \sqrt{2(M_{20}+M_{02}+\sqrt{(M_{20}-M_{02})^2 + 4{M_{11}}^2})}$$

$$r_2 = \sqrt{2(M_{20}+M_{02}-\sqrt{(M_{20}-M_{02})^2 + 4{M_{11}}^2})}$$

根据长短轴和中心点及偏角可以求出包含物体的斜框区域。

四、结果展示

红色点表示物体中心，黄色框是通过中心点、偏角和长短轴计算出四个顶点后画出来的。

五、代码

std::vector< std::vector< cv::Point> > contours;
std::vector<cv::Vec4i> hierarchy;
cv::findContours(cvImg, contours, hierarchy, cv::RETR_CCOMP, cv::CHAIN_APPROX_SIMPLE);
if (contours.size() > 0) {
	std::vector< cv::Point>cnt = contours[0];
	for (int i = 1; i < contours.size(); ++i) {
		if (contours[i].size() > cnt.size()) {
			cnt = contours[i];
		}
	}
        cv::Moments mu = cv::moments(cnt);
        cv::Point2f center = cv::Point2f(static_cast<float>(mu.m10 / mu.m00), static_cast<float>(mu.m01 / mu.m00));
}