主成分分析乱谈
首先要明白主成分并不是指原始的学习数据;其实所有的模型经过fit(X)之后获取的是模型;不要设想学习之后,可以通过模型来获得学习数据,这是没有意义的。
其次要明白成分(components)的概念,是指数据投影(projection)到低维的向量,其实在空间中一个数据模型是可以有多个投影的,但是每个投影的变化程度是不一样的,这个变化程度用下面的公式来计算,sigma是协方差矩阵的意思,数据变化的主方向就是协方差的主特征向量:
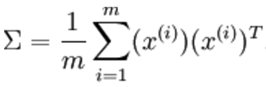
一个数乘以自己的转置矩阵;这个就是在demo中看到的:
C = pca.components_
R = C.T.dot(C)
这个R就是x的协方差;那么这个特征值越大他的成分排名就越靠前,指定的主成分数量之后,会按照特征值排序,按照从大到小取出。
在scikit中的PCA,在构造的时候你需要指定n_components,这个参数注意并不是主成分,而是因为一个模型将会有多个成分,取其中几个成分(这个就是component_的数据定义);主成分其实是只有通过求解R才能够获知,因为R的主特征值就是主成分;
最后,PCA是要降维的,所谓的降维就是将数据向各个主向量(主成分)投影;比如在demo中的z值:
z = (R[0, 2] * x1 + R[1, 2] * x2) /(1 - R[2,2])
z值就是将x1,X2的数据超平面的第三个维度。
看到上面的公式其实可以引申一下:对于一个X,shape:(m,p),m个样本,p个特征,那么p的协方差矩阵:
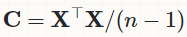
那看到了吗,这个和z值的公式是一致的;但是这个协方差矩阵成立的前提是X已经被中心化(centered);X.T.dot(X)是求方差,除以(n-1)是为了获取无偏估计。至于如何进行中心化,其实非常简单:
X -X.means()
参考
介绍PCA和SVD



