线性回归原理
首先要明白线性回归的基本公式:
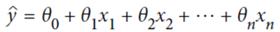
向量的表达公式就是:
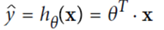
在机器学习里面,目标就是通过既有的X,y数据来推断出theta的值,来使得该公式最大化的接近点集区域;为了实现这个,采用的工具就是M均方差错误(Mean Square Error,MSE);就是让推断出来的theta和X的乘积于原始y数据之差尽量小;
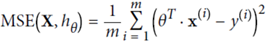
那么机器学习的过程就是求解theta,使得MSE的值最小,那么获取最小theta的公式就是:
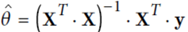
在代码实现层面上:
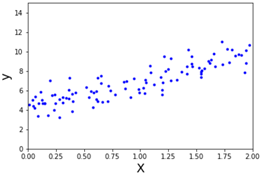
首先是构造一个随机点集:
import matplotlib.pyplot as plt import numpy as np import numpy.random as rnd X = 2* rnd.rand(100, 1) y = 4 + 3 * X + rnd.randn(100, 1) plt.plot(X, y, "b.") plt.xlabel("X", fontsize=18) plt.ylabel("y", fontsize=18) plt.axis([0, 2, 0, 15]) plt.show()
然后是计算最小theta:
1 import numpy.linalg as LA 2 X_b = np.c_[np.ones((100, 1)), X] 3 theta_best = LA.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) 4 print(theta_best)
output:
array([[4.20831857], [2.79226572]])
上面就是通过拉格朗日公式的inverse函数(inv)来进行逆矩阵的计算,转置矩阵通过T运算即可获得;这样就实现上面的获取最小theta的公式;获取的theta的值其实是theta0=4;theta1=3;
1 X_new = np.array([[0], [2]]) 2 X_new_b = np.c_[np.ones((2, 1)), X_new] 3 y_predict = X_new_b.dot(theta_best) 4 y_predict2 = X_new_b.dot(theta_best)
output:
array([[ 4.21509616],[ 9.75532293]])
X_new其实是X的值,上面这段代码的含义就是计算一下关于X取值0,2对应的y的取值;为什么会有X_new_b呢?其实从第一个公式可以看到,theta本质其实是X值得系数(model parameter),X0的值是固定1(所以公式第一位才会有theta0),X_new_b其实就是向X矩阵中增加一个1;这个输出的意义就是X=0, y=4.2; X=2, y=9。
不过有一点要注意,就是向量表达式其实是应该X乘以theta(图中给出的公式写法,在python实现中需要切换一下)。其实想一下,theta就是一列信息,其实他的形式和y的形式是一样(也是只有一列信息)。而结果的形式适合乘号的右侧是一致的。



