关于svm
svm的研究一下,越研究越发现深入。下面谈一些我个人一些拙见。
svm计算基础是逻辑回归(logistic regression),其实一切二元分类的鼻祖我觉得都是logistic regress。

公式如下:

那么当我们谋求一个超平面(在二维里面超"线")y = w.T * x + b来实现分类,其实就是g(w.T *x + b),注意这里有点反人类,在前者y是因变量,但是在g(z)中,y变成了自变量,是一个层级关系;后者意义就是我作为一个函数,函数的意义满足某个计算规则的点,扔到里面去,可以用于做分类;从下图可以看到,下面的三条线(超平面),都符合函数w.T + b的模式,但是扔到g(z)里面的结果预期是不一样,相当于将g(1)和g(-1),g(0)(注意这里的-1和1都是极值,为了保证最大间隔的极值,其实y是连续的,可以取任意实数);那么就是可以实现基于sigmoid函数的分类。当然g的取值也是二元的-1,和+1。

那么下面就是重点讨论w.T*x + b这个超平面。在讨论这个公式之前,我们首先确定一下概念,有了上图之后,可以简单的解释一下这个问题,所谓的支持向量机,就是实现查找到实现可分间隔最大化的边缘平面的算法;那么支持向量就是分布在变换平面上面的点,之所以称之为支持向量就是因为他么支撑了边缘平面,那么支持向量后面的那些点都不需要关心了,他们的位置对于分类没有任何帮助,所以就属于非支撑(骨干)的点。到此简单讲解了一下支持向量机的概念。
那么如何来搞掂这个最大化边缘平面呢?我在刚开始接触的时候其实并不是特别理解最大化间距,但是看到上图之后,其实你会发现如果不断的旋转移动这三条线,你会发现为了实现分类,三条线的相对位置其实是在不断变化的,svm的算法的目的就是实现让分类边缘线1)平行,2)间隔最大;那么为什么要最大呢?这样分类倾向性会更加明显一些,一些个似是而非的点可能性将会非常小;极端情况,在逻辑回归的场景下,就是一条线,如果点在这条线上面了,你说怎么分?所以svm通过"宽带"这种分割模式,在很大程度上加强的分类的倾向性。
关于最大化边缘平面距离就是最大化间隔问题,那么间隔,就要提到两种间隔,分别是函数间隔和几何间隔,函数间隔:

点x到超平面的间隔,或者说距离就是w.T *x + b,但是因为分类,所以距离有正负,为了获知分类正确性,前面乘以y,y就是分类,只有-1和1两个值,之所以这样处理,如果分类正确,说明y和f(x)的符号一致,距离必然正值,反之负值,所以通过符号就可以判断来准确性。我们让边缘平面的y值取-1和1,所以在边缘超平面的点一定是=1或者=-1,那么y的取值范围是大于1,小于-1的;通过函数间隔,其实我们目标是求出这些点到超平面的距离的最小值:

这样人为的定义的距离有一个问题,就是如果等比例放大w和b,将会导致距离也变化,但是我们知道等比例改变w和b将会导致距离变化(对应的y值也等比例增加),但是此时超平面并没有变化,但是距离却不再和之前相等;所以此时引入了几何距离:

下面的是推导过程,可以得出几何距离。

处于同样的理由,我们让y*r,这个就是最终的几何距离公式:

这样我们求解最大间隔问题,其实就是求:

约束条件(s.t)为

这样,我们其实设r^值为1,并不影响优化效果,来简化处理公式(为什么改成1可以?):

那么如何求解呢?
这里有一个非常美妙的变化,就是上面的公式可以变型为min函数:
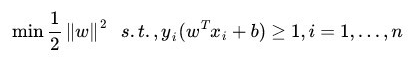
更加精妙的变形在于通过下式将约束和min函数包容起来了:
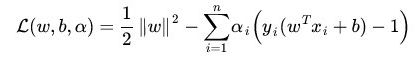
其实为什么可以把约束和主题函数放在一起?看下面的公式:

ai是大于0的,yi(w.T*xi+b)一定是>=1,因为为了实现L(w,b,a)的最大化,一定是||w||**2/2的后面部分一定是等于0,才能够实现最大化,所谓约束,拉格朗日对偶的公式里面已经成为了一种前置假设。这个是我之前的理解,但是这里其实牵涉到凸优化的问题,并不是简单的极值。比如下面的变形,其实使用的凸优化的知识:
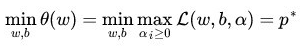
然后进行max和min位置交换:

这种等价交换是有条件的(正常情况下d*<=p*),这种转换使得计算变得简单,但是,为什么变得简单了,为什么先min后max就会简化运算?不懂。
数学最优化模型是下图所示,f(x)是要求最小化的函数,hj是等式约束,gk是不等式约束。

有了有了优化模型的描述,我们再来看看min-max等价交换的KKT条件:
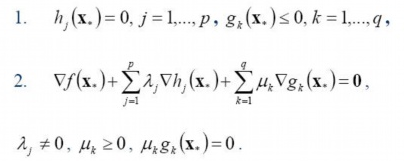
求对偶问题三个步骤:
1)对w和b求对偶:

带入到上面L(w,b,a)公式中,可得:

最后经过推到:
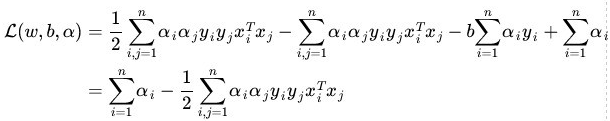
这里注意,早期全部都是i但是到了推倒的最后几步出现了i,j的分割:
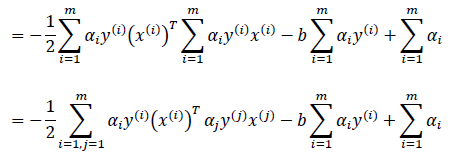
这里的其实是一个两层循环,外层循环是i,里层循环是j;这个两层循环的累加完成了矩阵间的乘法运算。
第二步,根据上一步推导出来的公式进行求a值;

有了a之后,根据偏导数求出的公式可以解出w,然后通过下面的公式可以求出b,从公式上面来看应该是f(x)的最大值和最小值的均值,但是为什么是这个求b值呢?
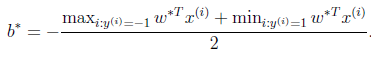
第三步,即最后一步,通过SMO算法求解a;但是到这里我懵逼了,在第二步的时候,不是已经把a值给求出来了吗,怎么又求了一遍?
核函数
其实数据大多数场景都是线性不可分的,就是无法采用一条直线进行分类,需要曲线,曲线就是多项式,计算比较复杂,这个时候,如果是升维,那么很多时候可以简化问题,这个时候,核函数就出现了。
在讲核函数之前,我们先看一个前置知识:向量内积。
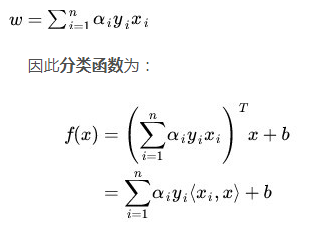
通过上面公式,可以很清晰的看到转置被处理成了内积,OK,核函数的本质其实就是把低维数据映射高维数据,怎么映射?
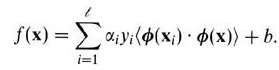
简单讲就是将原来x->φ(x),那么核函数的高明之处在于他的计算并不是在映射到高维之后,再计算,如果那样的话,求解可能会有"维度灾难"。比如:
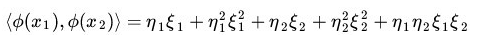
这是一个五维空间,计算量比较大了,但是核函数不是对于分解之后在计算,而是找到了一种等价的形式:

来对其进行计算,这样的话,你会发现计算简单很多。而且核函数的形式和咱么上面提到公式中内积的形式是一致的(注意,核函数可并不是为了svm的内积而生的,而是有气自己数学应用场景的)。所以,你可以指定一些核函数来进行提升维度处理,同时还避免了高维的海量特征的计算。
常用的核函数包括:
1. 多项式;上面举例(<x1,x2> + 1)**2就是一个多项式核函数的例子;
2. 高斯核函数,这个可能是应用最广泛的一种和函数了。
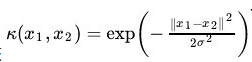
3. 线性核函数,这个主要就是用于兼容,当不需要提高维度,但是为了计算的统一性,采用这个核函数可以保证计算逻辑的一致性。
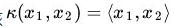
关于松弛变量
svm中对于离群点有专门的处理,所谓离群点是指下图中的蓝色部分。所谓离群点是指貌似对方,但是其实是自己人那些点,但是因为位置比较尴尬,所以svm设置了一个松弛变量,就是允许在一定范围内的离群点,这样可以这样讲,其实允许在"宽带"之间有一些点,这些点将会基于到宽带两边的距离来进行划分。避免宽带间点无法被处理。
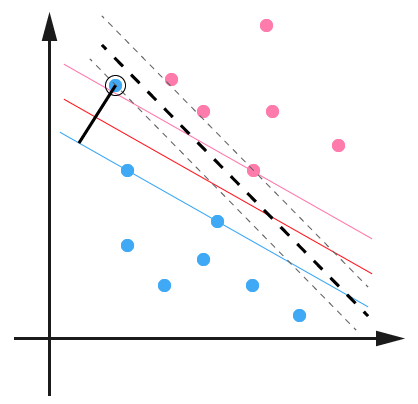
我们继续拿函数距离来做表达(为什么这里又采用了函数距离,而不是集合距离),此时距离赢不再是1,而是减去一个变量。

ξi不可以任意大的,于是添加了一个C作为限制

于是我们有了新的L(w,b,a):

后面处理的流程和上面很类似,首先是求导获取极值取值:
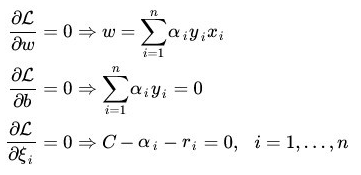
带入到拉格朗日的公式中,可以求得:
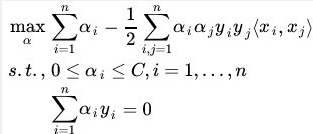
结果函数和之前是一样的,但是增加了一项约束:ai<=C(因为C-ai-ri=0,所以C必然大于等于ai)
最后是SMO算法,其实smo算法才是向量机的核心,他解决了如何求解a的关键,但是讲真,我看的资料并没有把smo算法讲明白。下一轮再研究吧。
参考
https://blog.csdn.net/v_JULY_v/article/details/7624837



