关于Adaboost算法
我花了将近一周的时间,才算搞懂了adaboost的原理。这根骨头终究还是被我啃下来了。
Adaboost是boosting系的解决方案,类似的是bagging系,bagging系是另外一个话题,还没有深入研究。Adaboost是boosting系非常流行的算法。但凡是介绍boosting的书籍无不介绍Adaboosting,也是因为其学习效果很好。
Adaboost首先要建立一个概念:
弱分类器,也成为基础分类器,就是分类能力不是特别强,正确概率略高于50%的那种,比如只有一层的决策树。boosting的原理就是整合弱分类器,使其联合起来变成一种"强分类器"。
在Adaboost中,就是通过训练出多个弱分类器,然后为他们赋权重;最后形成了一组弱分类器+权重的模型,
那么,关键来了怎么选择弱分类器,怎么来分配权重?据说弱分类器可以是svm,可以是逻辑回归;但是我看到资料和描述都是以决策树为蓝本的。
要想要搞懂adaboost,还要搞懂他的两个层级的权重,第一个权重是上面我们讲到的分类器的权重,成为alpha,是一个浮点型的值;
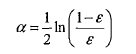
什么是ε?我们下面会讲到。
另外一个是样本权重,称之为D,是一个列向量,和每个样本对应。首先讲一下样本权重,在一个分类器训练出来之后,将会重新设置样本权重,首个分类器他的样本权重是一样的,都是1/sample_count,然后每每次训练完,都会调整这个这个样本权重,为什么?我们继续沿用决策树说事。调整的策略就是增大预测错误的样本的权重,为什么?样本权重只有一个作用,就是计算错误权重,错误权重errorWeight=D.T * errorArr,errorArr是预测错误的列向量,预测正确的样本对应值0,预测错误的为1,样本权重D就是做件事情,那么对于决策树模型而言,本轮某个特征判断错了,那么样本其实就上了黑名单,用数学表示就是这个这个样本的权重将会增加,
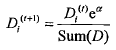
样本权重增加导致了什么?其实不会导致什么,即使说明了某个样本的错误比重要增加。所谓错误权重,都是判断错误,如果历史某个样本已经判读出错过一次,那么这个样本如果再错,它的错误权重就要增加,这种权重的改变(D中元素wi的总和不变,保持为1),将会导致weighterror值更加有意义,判定最小weighterror也会更加准确。如果判断对了,会相应的减小样本的权重。
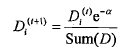
回过头来,什么是ε?在内层循环中,会遍历所有特征,然后从最小值到最大值往上加特征值,在判断该特征值下,分类的准确性,然后会记录下来该特征下最小错误率,针对每个特征的这个最小错误率当然是局部的错误率;针对于所有的特征的的最小错了率之间再取最小就是全局的错误率,ε就是这个全局错误率。
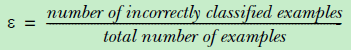
两层的权重介绍完了,基本算法也就明了了,内层的算法是遍历样本中的每个特征,然后再从特征值的最小值开始尝试进行分类,逐渐按照等量增加特征值不断地尝试分类一直达到最大值,走完了一轮特征,换下一个特征,在逐次增加特征值...计算下来每次尝试的错误权重,记录下来最小的错误权重的信息,信息包括:特征列索引,特征值以及逻辑比较(大于还是小于),当把所有的特征跑完一遍,到此,一个分类器就横空出世了,设么是分类器?本质就是最小错误权重的信息,就是分类器。
作为外层算法,是一个循环调用内层算法的过程,每当获得了一个分类器,都要为他计算权重,权重alpha的计算公式上面已经给出,总之和最小错误权重有关系,错误权重越小,分类器的权重越高,说明是优质分类器(相对的),反之亦然;然后就是累加权重alpha*预测值classEst,累加的目标就是sign和真实的分类器一致,注意是符号一致,真实分类器只有-1,1两种值。如果一致了,退出循环;不一致,说明还要再引入分类器,此时再来计算D值(参见上文公式),然后基于D值再来调用内层算法。
这样不断获得分类器,直到分类一致(或者循环次数达到指定次数)。外层算分目的是获取到一组分类器,这组分类器是经过训练,实现了全来一遍,就可以保证累加权重预测值之和的符号(sign)和真实的分类一致。
有了这组分类器,即adaboost classifieies,那么就可以进行分类了。
首先是获取训练数据集,然后通过外层算法获取到adaboost classifieies(组分类器),这个是训练过程;获得了组分类器之后,在获取测试数据集,然后遍历分类器,让每个分类器都对这批测试数据进行分类,每个分类器都会使用自己最好的分类方式(权重错误最低)来进行分类,即根据指定的特征,利用指定特征值进行比较分类;得到的分类结果(-1,1集合)将会乘以他们的权重(alpha),成为权重分类向量(weightClassEst);然后将各个分类器的权重分类向量进行累加(aggClassEst),最后取aggClassEst的符号作为分类结果。到此,分类结束。



