分类器以及归一化

分类器的本质是什么？其实就是根据近邻算法来判断是否属于同一个区域范围；

近邻算法的本质是什么？是距离，距离分两种，一种是曼哈顿距离，一阶算法；另外一种是欧式距离，二阶算法；

距离怎么判断？对于监督学习，已经知道了几种分类，那么针对这些分类，距离那个分类（样本）近，就是什么分类。

所以推演到这里离，分类器计算本质其实就是根据特征来计算和已知分类样本的距离，距离那个分类样本更近，就是什么分类。

那么物品的距离怎么来算，我们知道可以通过欧式/曼哈顿距离来求，但是怎么计算物品间距离？特征，根据特征来计算距离。物品间的距离就是各个特征之间距离的某种形式的累加（求差再求和—曼哈顿，或者求差平方再求和再开放—欧式）。

但是在计算的时候有问题，那就是不同特征之间的数量级可能不同，比如身高是1~2（m），但是收入确实5000~100000（元），这会导致一个问题，就是量纲小的特征的比重将会变小，无形间好像把量纲大的赋予了极大的权重，但是这个并不是我们想要的。于是这里引入了归一化（normalization），归一化的目的就是要将特征等比例将大量纲的特征的取值范围，按照某种规则映射为范围 [-1, 1]；这样大家的量纲就接近了。

归一化的计算过程

首先求取均值；

然后，求取标准差

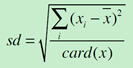
最后计算标准分

没完事，在归一化的过程中同样有的时候，对于同一个特征，他是会有一些离群点，这些点将会导致求取平均值的时候严重拉高拉低均值，这个时候就需要采用中位数的方式来替换"均值"；中位数就是将数据从小到大排列，取中间的一位（奇数）或者两位数（偶数）的均值来作为"mean"。