常见排序算法整理(python实现 持续更新)
1 快速排序
快速排序是对冒泡排序的一种改进。
它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
比如:

以最后一个数字4 为基准数,将比4小的数字放到左边,比4大的数字放到右边。
然后对左右2发个数组继续按上述的方法进行排序。
代码如下:
def quick_sort(lst):
if len(lst) <= 1:
return lst
left, right = [], []
data = lst.pop()
for i in lst:
if i < data:
left.append(i)
else:
right.append(i)
return quick_sort(left) + [data] + quick_sort(right)
if __name__ == "__main__":
array = [2, 3, 5, 7, 1, 4, 6, 15, 5, 2, 7, 9, 10, 15, 9, 17, 12]
print(quick_sort(array))
2 选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。
代码如下:
def choice_sort(lst):
new_lst = []
while len(lst) > 0:
smallest = min(lst)
new_lst.append(smallest)
lst.remove(smallest)
return new_lst
if __name__ == "__main__":
array = [2, 3, 5, 7, 1, 4, 6, 15, 5, 2, 7, 9, 10, 15, 9, 17, 12]
print(choice_sort(array))
3 冒泡排序
冒泡排序它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素已经排序完成。
-
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
-
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码如下:
def bubble_sort(lst):
lenght_lst = len(lst)
while lenght_lst > 0:
for i in range(lenght_lst-1):
if lst[i] > lst[i+1]:
lst[i], lst[i+1] = lst[i+1], lst[i]
lenght_lst -= 1
return lst
if __name__ == "__main__":
array = [2, 3, 5, 7, 1, 4, 6, 15, 5, 2, 7, 9, 10, 15, 9, 17, 12]
print(bubble_sort(array))
4 插入排序
有一个已经有序的数据序列,要求在这个已经排列好的数据中插入一个数,但要求插入后数据序列依然有序,这个时候就需要用到一种新的排序方法,插入排序法。
插入排序的基本操作就是将一个数据插入到已经排好的有序数据中,从而得到一个新的,个数加一的有序数据,算法适用于少量数据的排序。
插入排序的基本思想是:每步将一个待排记录,按照关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。
插入排序的核心在于,它把一个无序数列看成两个数列,假如第一个元素构成了第一个数列,那么余下的元素构成了第二个数列,很显然,第一个数列是有序的(因为只有一个元素嘛,肯定有序哦),那么我们把第二个数列的第一个元素拿出来插入到第一个数列,使它依然构成一个有序数列,直到第二个数列中的所有元素全部插入到第一个数列,这时候就排好序了。
代码如下:
def cha_sort(lst):
lenght_lst = len(lst)
for i in range(1, lenght_lst):
for j in range(i, 0, -1):
if lst[j] < lst[j-1]:
lst[j], lst[j-1] = lst[j-1], lst[j]
return lst
if __name__ == "__main__":
array = [2, 3, 5, 7, 1, 4, 6, 15, 5, 2, 7, 9, 10, 15, 9, 17, 12]
print(cha_sort(array))
5 希尔排序
希尔排序是插入排序的一种改进方法。希尔排序是一种非稳定的排序方法。
基本思想先取一个小于n的整数d1作为增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在组内进行插入排序,然后取第二个增量d2<d1,重复上述的分组和排序,直至索取的增量dt=1,即所有记录放在同一组中进行直接插入排序为止。
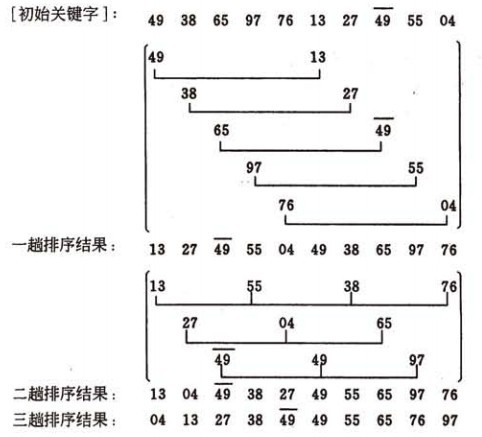
3趟排序的增量分别为5,3,1.
第一趟的增量d1=5, 将10个待排记录分为5个子序列,分别进行直接插入排序,结果为(13, 27, 49, 55, 04, 49, 38, 65, 97, 76)
第二趟的增量d2=3, 将10个待排记录分为3个子序列,分别进行直接插入排序,结果为(13, 04, 49, 38, 27, 49, 55, 65, 97, 76)
第三趟的增量d3=1, 对整个序列进行直接插入排序,最后结果为(04, 13, 27, 38, 49, 49, 55, 65, 76, 97)
代码如下:
def shell_sort(lst): length = len(lst)//2 #初始步长,要用地板除,确保为正整数 while length > 0: for j in range(length, len(lst)): while j >= length and lst[j] < lst[j-length]: #间隔为length的后数字小于前数字 lst[j-length], lst[j] = lst[j], lst[j-length] #做插入 j -= length #不要遗漏元素 length //= 2 # 步长每次减小一倍 return lst if __name__ == "__main__": array = [2, 3, 5, 7, 1, 4, 6, 11, 9, 10, 8] print(shell_sort(array))
6 归并排序
归并排序是建立在归并操作上的一种有效的排序算法.该算法是采用分而治之的一个典型应用,将已有序的子序列合并,得到完全有序的序列,即先使每个子序列有序,再使子序列段间有序,将两个有序表合成一个有序表,称为二路并规。
1. 从下往上的归并排序:将待排序的数列分成若干个长度为1的子数列,然后将这些数列两两合并;得到若干个长度为2的有序数列,再将这些数列两两合并;得到若干个长度为4的有序数列,再将它们两两合并;直接合并成一个数列为止。这样就得到了我们想要的排序结果。(参考下面的图片)
2. 从上往下的归并排序:它与"从下往上"在排序上是反方向的。它基本包括3步:
① 分解 -- 将当前区间一分为二,即求分裂点 mid = (low + high)/2;
② 求解 -- 递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。递归的终结条件是子区间长度为1。
③ 合并 -- 将已排序的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]
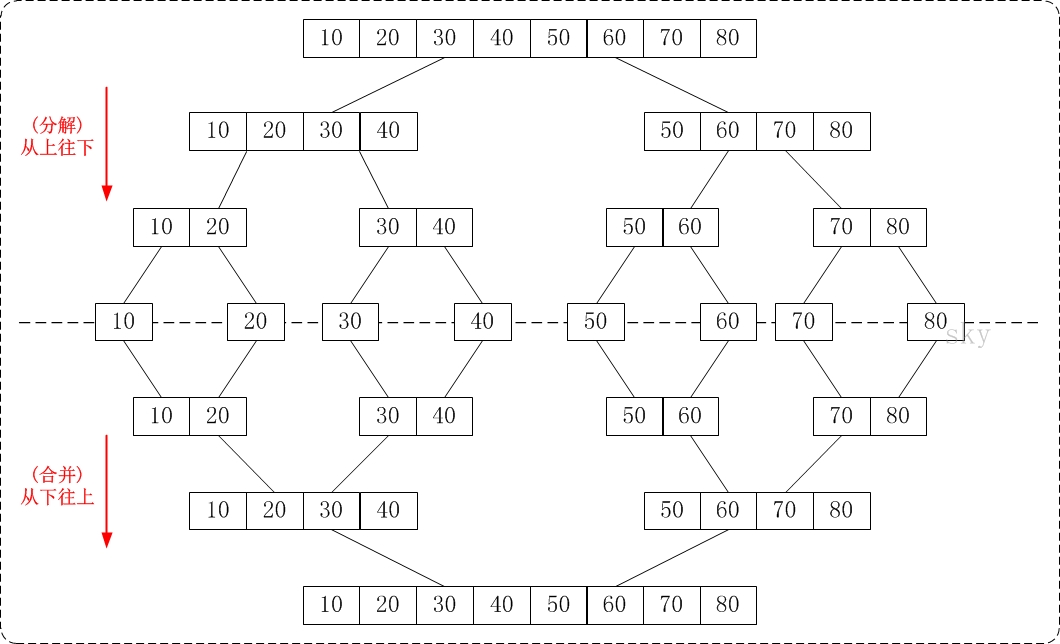
以下采用的是从上而下的归并排序。
假如我们有一个n个数的数列,下标从0到n-1
首先是分开的过程
1 我们按照 n//2 把这个数列分成两个小的数列
2 把两个小数列 再按照新长度的一半 把每个小数列都分成两个更小的
。。。一直这样重复,一直到每一个数分开了
比如: 6 5 4 3 2 1
第一次 n=6 n//2=3 分成 6 5 4 3 2 1
第二次 n=3 n//2=1 分成 6 5 4 3 2 1
第三次 n=1的部分不分了
n=2 n//2=1 分成 5 4 2 1
之后是合并排序的过程:
3 分开之后我们按照最后分开的两个数比较大小形成正确顺序后组合绑定
刚刚举得例子 最后一行最后分开的数排序后绑定 变成 4 5 1 2
排序后倒数第二行相当于把最新分开的数排序之后变成 6 4 5 3 12
4 对每组数据按照上次分开的结果,进行排序后绑定
6 和 4 5(两个数绑定了) 进行排序
3 和 1 2(两个数绑定了) 进行排序
排完后 上述例子第一行待排序的 4 5 6 1 2 3 两组数据
5 对上次分开的两组进行排序
拿着 4 5 6 1 2 3两个数组,进行排序,每次拿出每个数列中第一个(最小的数)比较,把较小的数放入结果数组。再进行下一次排序。
每个数组拿出第一个数,小的那个拿出来放在第一位 1 拿出来了, 变成4 5 6 2 3
每个数组拿出第一个书比较小的那个放在下一个位置 1 2被拿出来, 待排序 4 5 6 2
每个数组拿出第一个书比较小的那个放在下一个位置 1 2 3 被拿出来, 待排序 4 5 6
如果一个数组空了,说明另一个数组一定比排好序的数组最后一个大 追加就可以结果 1 2 3 4 5 6
相当于我们每次拿到两个有序的列表进行合并,分别从两个列表第一个元素比较,把小的拿出来,在拿新的第一个元素比较,把小的拿出来
这样一直到两个列表空了 就按顺序合并了两个列表
代码如下:
def merge_sort(lst):
if len(lst) <= 1:
return lst
num = len(lst) // 2
left = merge_sort(lst[:num])
right = merge_sort(lst[num:])
return merge(left, right)
def merge(left, right):
l, r = 0, 0
result = []
while l < len(left) and r < len(right):
if left[l] < right[r]:
result.append(left[l])
l += 1
else:
result.append(right[r])
r += 1
result += list(left[l:])
result += list(right[r:])
return result
if __name__ == "__main__":
array = [2, 3, 5, 7, 1, 4, 6, 11, 9, 10, 8]
print(merge_sort(array))
算法总结:
要理解算法的复杂度,肯定首先要了解大O表示法,大O表示法是一种特殊的表示法,指出的算法的速度有多快。
| 冒泡排序 | 稳定 | O(n²) |
| 快速排序 | 不稳定 | O(N*logN) |
| 插入排序 | 稳定 | O(n2) |
| 希尔排序 | 不稳定 | O(n^(1.3—2)) |
| 选择排序 | 不稳定 | O(n2) |
| 归并排序 | 稳定 | O(NlogN) |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号