2023-2-6 #34 我渴望的夏季 太热烈太清晰

——小夏Elin《无夏之城》

最近在摆，没更博！

189 CF1718E Impressionism

谔谔题，不妨令 \(n\leqslant m\)。

用二分图刻画这个问题，无非是求两个带边权的特殊二分图是否同构。

一个暴力的想法是对于左部每个连通块，任意选择一个点并枚举右部一个未对应上的点看看能不能映射，遍历一遍连通块就可以 check 合不合法。

事实上加一个剪枝：只枚举左部点数相同的连通块，这样就能做到 \(O(n^2m)=O(nm\sqrt{nm})\)。（原因是，每个目标图右部点被遍历的次数为其连通块中左部点的数量乘上原图中同大小左部点连通块数量，这个求和是不超过 \(n\) 的，而原图右部点复杂度证明是一样的）

190 PE821 123-Separable

显然要分连通块做这件事，显然大小相同的连通块完全一致，我们只须处理出每个连通块大小对应的答案。（由于连通块大小不超过 \(1000\)，可以本地打表）

考场写了个调整可以跑 \(n\leqslant 10^{12}\)，\(n=10^{16}\) 大概比答案只少几百。

正解大概是小的时候跑指数暴力，大的时候考虑一个策略：（听说指数也能跑 \(10^{12}\)）

可以证明一件事：所有黑框一定有一个格子不被选中，具体我们可以分讨覆盖某些格子的方式得到这一点。

当然也存在 corner case：若轮廓线恰好切掉某个黑框一个非第一行第一列的格子，我们可以通过空出那个格子来换另一个格子被覆盖。

这个时候 \(2^{3k+1}\cdot 3\leqslant n,2^{3k+2}\cdot 3>n,2^{3k+3}\leqslant n\)，判一下就好了。

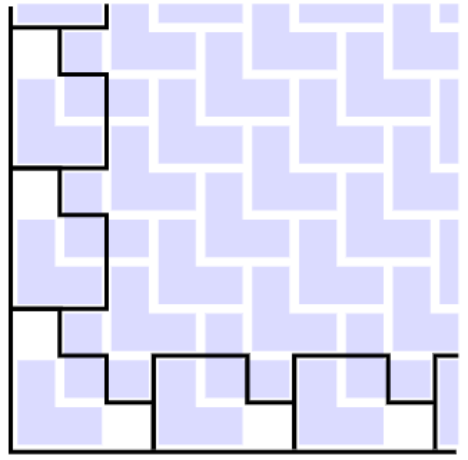
我们的构造非常优秀，除了左下的框外都能达到下界，事实上爆搜结果告诉我们在 \(n\) 较大时为了使答案最大化，左下的框也有两个不能选，证明我也不会！！

191 百度之星2022 复赛 E 项链

写一个题意：给定若干数字串，总长不超过 \(50\)，对于所有 \(i\in[1,n]\) 计数长度为 \(i\) 的数字串数量，满足至少包括一个数字串，视旋转同构为同构。（不视翻转同构同构）

\(n\leqslant 5\times 10^4\)。

我不会群论了！

根据 Polya 定理：（\(|S/G|\) 就是 \(S\) 在 \(G\) 作用下形成的等价类数量）

\[|S/G|=\frac1{|G|}\sum_{g\in G}V^{c(g)} \]

那么答案就是：

\[\frac{1}{n}\sum_{i=1}^nf_{\gcd(i,n)}=\frac1n\sum_{d\mid n}f(d)\sum_{k=1}^{\frac nd}[\gcd(k,\frac nd)=1]=\frac 1n(f*\varphi)(n) \]

直接 ACAM 上 dp 就能过，复杂度 \(O(nm|\Sigma|)\)。（记 \(m=\sum|S|\)）

正解做法很诡异，我们将 ACAM 转移矩阵写作 \(A\)，无非是求 \(A^{1,2,\cdots,n}\) 的迹。

类似光速幂，我们可以将 \(A^k\) 拆成 \(A^p\times A^{q\lfloor\sqrt n\rfloor}\)，且 \(p\leqslant \sqrt n\)，可以直接暴力矩阵乘法预处理这根号个矩阵。由于迹只牵扯对角线元素，我们可以 \(O(k)\) 计算每个元素，复杂度 \(O(nm^2+\sqrt nm^3)\)。