2023-1-20 #29 “不会有全世界陪你沉睡的童话”

——霾《绝世丑角》

昨天 vp：ICPC2022 Nanjing。

K 题比较弱智，但是后面摆了，懒得写。

本来录屏了，后来感觉打的不太行就删掉了。

160 C Fabulous Fungus Frenzy

神秘题，感觉并不会往这个方向思考。

时光倒流，盖章操作变成“对于一个特殊的子矩阵，将其全部变成通配符”。

可以发现盖章操作一定不会变劣，所以我们可以任取一个章，只要盖了能有新的通配符就盖，这样盖章次数肯定不会超过 \(nm\)，满足限制。（因此，我们可以每次选择一个章盖到没法出现通配符为止，之后就不需要考虑这个章了）

由于操作次数限制很宽松，我们不妨把章统一放在左上角盖，每次用交换操作暴力把字符交换上来。

暴力实现就能过。

161 E Color the Tree

很难的啊！没想到大家都会做。

可以发现不同层的结点互不干扰，我们不妨枚举每一层，把每一层的答案加和。

我们建出第 \(d\) 层结点对应虚树，只需 dp 当前子树所有叶子被染色的最小代价，这个很好处理。

复杂度 \(O(n\log n)\)，当然也可以线性。

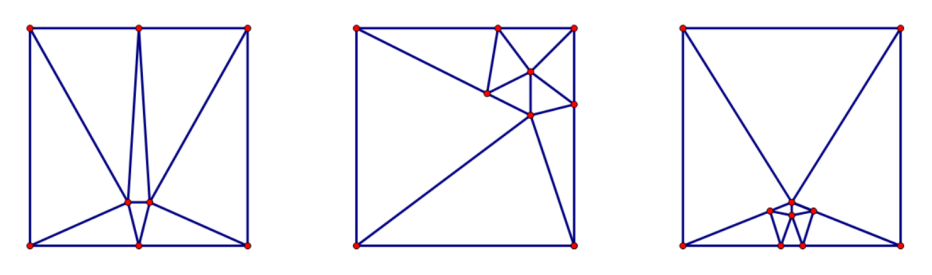
162 F Triangles

MO 题为啥要出 ACM 里来。

一个很好的策略是连接某个锐角三角形三边中点，这样锐角三角形数量会加三。

可以证明 \(n\leqslant 7\) 无解，我们只需构造出 \(n=8,9,10\) 的解。

163 H Factories Once More

其实比较简单，只是之前有一道类似的正睿题没做出来比较丢人，所以记录一下。

dp 每棵子树选多少个结点的最大权值，一条边的经过次数就是较深子树中选定点数量。

列出转移方程，它是先做一个二次函数加，然后闵可夫斯基和。归纳证明 dp 数组是上凸的，维护差分值，只需支持等差数列加，以及启发式合并，使用 splay 启发式合并即可 \(O(n\log n)\)。

164 J Perfect Matching

不难，不过有意思。

观察可知 \(|a_i-a_j|=|i-j|\) 等价于 \(a_i+i=a_j+j\) 或者 \(a_i-i=a_j-j\)。

建立二分图，左边代表 \(a_i+i\) 右边代表 \(a_i-i\)，原序列一个下标对应一条边。

那么无非就是构造无向图图相邻边的匹配，这个的结论是每个连通块边数为偶数就有解，构造随便 dfs 树一下就好了。

165 L Proposition Composition

WC 刚讲过！

别急。还不会。

填坑指路。

166 APC001 H Generalized Insertion Sort

一个比较特殊的切入点：leafish 结点。

我们定义 leafish 结点为：子树只有一个叶子节点的结点，可以发现 leafish 结点是若干从叶子上来不交的链。

如果我们每次删除掉一棵树所有 leafish 结点，那么删除次数是 \(O(\log n)\) 的，原因是每次都会删掉所有底层重链。

接下来讲这题做法：

不妨先考虑链怎么处理，类似插入排序，增量地维护有序后缀，每次把根的权值插入到对应位置上。

尝试扩展到处理所有 leafish 结点：我们仍然增量地维护每个有序后缀，如果根上权值对应点是 leafish 的，就插入到对应位置。否则，我们尝试找一个“垃圾桶”，把权值放在这里。

一个很好的选择是某个未复原的 leafish 权值下方，此时我们可以将放垃圾桶次数均摊到 leafish 结点数量上。

那么删除掉所有 leafish 结点只需不超过 \(n+\#leafish\) 次，总操作次数 \(O(n\log n)\)。

167 CF1770H Koxia, Mahiru and Winter Festival