2022-12-11 #9 再异口同唱 那告别曲 逝去的一身葱茏
——校长《无理无智》
43 AT_mujin_pc_2017_d Oriented Tree
头痛,想不了题。。。
大概就是在直径中点断开,然后每棵子树都 dp 一下。
先放一边吧。
44 P4899 [IOI2018] werewolf 狼人
套路地建出小根的 Kruskal 重构树与大根的 Kruskal 重构树,那么人形能经过的结点就是小根重构树的一棵子树,狼形亦然,那么就是查看两棵子树是否有公共点,二维数点即可。
复杂度 \(O(m\log m)\)。
45 P4898 [IOI2018] seats 排座位
一个转化是 \((maxr-minr+1)(maxc-minc+1)-cnt=0\),由于其一定非负,所以是数最小值个数。
通过兔队线段树维护???buhui。。
想点靠谱的做法,根据 CF1270H Number of Components 中的技巧,我们可以尝试维护某些微观结构的数量。
仔细想想,首先,若 \([0,V]\) 合法则不能存在一个 \(>V\) 的数附近有两个及以上 \(\leqslant V\) 的数,而且有且仅有一个 \(\leqslant V\) 的数的左、上都 \(>V\)(或边界)。
每个位置作为这些结构都会对一段值域区间贡献,线段树维护即可,复杂度 \(O(n\log n)\)。
46 P5044 [IOI2018] meetings 会议
很容易得到一个平方做法,建出笛卡尔树,每次询问在笛卡尔树遍历计算每个位置贡献。
根据 P3246 [HNOI2016]序列 的技巧,我们不妨考察区间第一次被劈开的笛卡尔树结点,容易发现两边互不影响。那么我们只需对于每个笛卡尔树结点 \([l,p,r]\) 维护每个 \([p,q]\)(或 \([q,p]\)) 的答案就好了。
这事实上也就是维护每个结点的前缀、后缀的答案。
考虑合并的过程,我们要进行一次加法,以及一次对一次函数 chkmin,直接做是 \(O(n\log^2 n)\) 的。
由于斜率一定不超过当前根结点的权值,所以一次函数与原函数的交点至多一个,这样复杂度就是 \(O(n\log n)\) 了。
47 CF472G Design Tutorial: Increase the Constraints
汉明距离就是按位减的平方和,那么只需维护平方和与点乘结果。
点乘是很难处理的,一个经典的方法是分块 FFT,散块暴力,整块可以用一次差卷积处理所有答案,复杂度 \(O(n\sqrt{n\log n})\)。
但听说 bitset 可以直接草过去。
48 P6881 [JOI 2020 Final] 火事
比较难的。
不妨画出一个三角形,第 \(i\) 列第 \(j\) 行表示 \(\max_{k=i-j+1}^i a_k\):
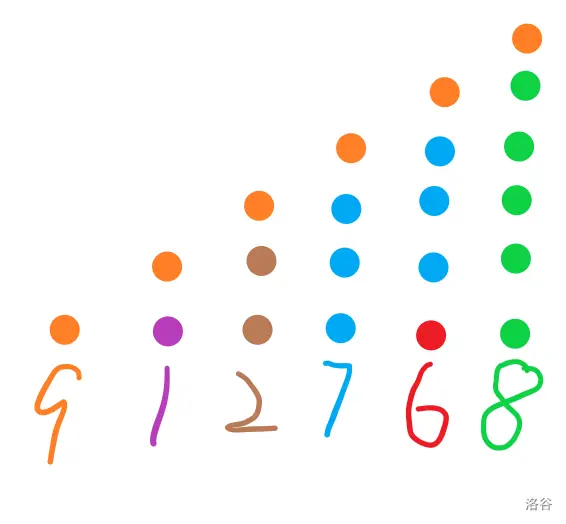
(from xtx1092515503)
可以发现,每个颜色的贡献都是一个平行四边形,而这个平行四边形的端点是很容易得到的,正反各做一遍单调栈就好了。
平行四边形加法,可以差分成三次三角形加法,平行于 \(x\) 轴的线段查询也可以差分成两条射线查询。于是类似维护历史版本和维护一下系数就好了,树状数组即可实现。
复杂度 \(O(n\log n)\)。
49 P5103 [JOI 2016 Final]断层
时光倒流,只需求出每一条边反向操作这么多遍后的 \(x\) 坐标。
旋转坐标系,这样两维就直接分开了。单独考察某一维,这一维的坐标大小关系一定不会改变,于是操作都是前缀加法,树状数组维护即可。
复杂度 \(O(n\log n)\)。
50 P7407 [JOI 2021 Final] ロボット
不是很难。
两种策略:把自己改成别的颜色、把同色边全部改颜色。注意策略一不合法的时候,边的颜色互不相同,因此策略二没有代价,因此不需要考虑这种情况。
一个例外是连续走两条同色边,且分别使用策略一、二,此时可以少一个策略一的代价,那么我们每个点的每个颜色建个虚点,进去代表使用策略一,出来代表使用策略二就好了。
复杂度 \(O((n+m)\log(n+m))\)。
51 CF526E Transmitting Levels
预处理出每个点能跳的最远距离 \(f_i\),那么若确定起点,每次都可以贪心跳尽量远,做到 \(O(ans)\) 复杂度。
你可能想,能不能利用 集训队互测2022-2023 D7T1 foo~ 的技巧优化,但由于你做一次的复杂度并不固定,你也不知道你要做多少次,所以比较困难。
观察可知对于任意位置 \(i\),一定有一个断点处于 \([i,i+f_i]\)。不妨取 \(f\) 最小值位置 \(k\),在 \([k,k+f_k]\) 中枚举起点,由于每一步长度都大于 \(f_k\),步数一定不会超过 \(\lceil\frac n{f_k}\rceil\),那么就做到了线性。
另一种做法:好吧懒得学,先 mark 在这里。
52 AT_tenka1_2017_f ModularPowerEquation!!
无语了,这都不会。
可以发现一定有解,我们递归地构造,不妨取 \(y\) 使得 \(y\equiv x\pmod{\varphi(m)},a^y\equiv x\pmod m\)。
那么此时有 \(a^y\equiv y\pmod{\gcd(m,\varphi(m))}\),递归求解即可。(可以发现递归到底层一定有解)
复杂度瓶颈在计算 \(\varphi(m)\) 上,预处理 \(\sqrt m\) 内的素数,这样做一次复杂度能除一个 \(\log\)。
复杂度 \(O(\sqrt m+T(\frac{\sqrt m}{\log m}+\log m))\)。
其实今天也比较颓啊。。。
始终无法达到自己理想中的状态。


