P8554 心跳 解题报告
P8554 心跳 解题报告:
题意
定义一个排列上的函数 表示序列 去除 位置后前缀最大值个数。对于所有长度为 的排列 ,生成序列 。试计数值域 ,且能被生成的 序列数量。
。
分析
hzr 场切了,有点恐怖的。
下面记 为不去除任何位置的前缀最大值个数。
首先有一个结论,对于两个 不相等的排列,其生成的 序列不可能有交。
经过初步地观察,我们能得知:
- 若去除的位置不是前缀最大值,;
- 否则, 为 后面大于 所有数的单调栈大小加 。
于是我们可以将序列里的数分成三个部分:前缀最大值,可能成为前缀最大值的数(下文称其为有用的数),其他。
将排列按照前缀最大值划分成若干段,那么前缀最大值的 就是其对应段有用的数数量加上 。
我们并不关心有用的数的位置,只关心其数量,于是可以将一段内所有有用的数保留顺序提前,然后生成一个仅包含 的序列, 对应前缀最大值, 对应有用的数, 对应没用的数。(称这种序列为颜色序列)
我们想直接 dp 来计数颜色序列,但必须先知道任意颜色序列是否都存在一个对应的排列 。
考虑一种排列的生成方式:从前往后加入数字,维护目前前缀 离散化后的结果,每次插入一个 内的数字并将大于等于其的数字加一(其实就是在值域上插入数字)。那么插入 就对应插入一个 ,插入 就对应插入一个 ,否则就是插入一个 。
只需保证第一个位置是 ,第二个位置是 即可。
但是不同的颜色序列可能对应相同的 序列,算重的原因实际上就是 与 等价,以及 与 等价(),于是我们只需保证序列中不存在 子段与 后的 子段即可。
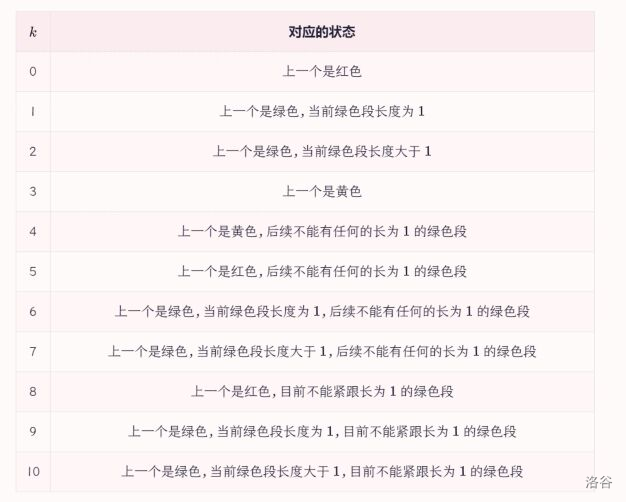
令 表示 dp 了 个位置,前缀最大值个数为 ,上一个为 、(长度 )、(长度 )、,无限制、当前段不能只有 个 ,后面所有段不能只有 个 ,直接转移即可。
的限制很好处理,要么前缀最大值数量大于 ,要么前缀最大值数量等于 且没有一个前缀最大值段没有有意义的数,随便改改转移方程就好了。
复杂度 。
代码
写不动,借鉴了官方题解的波特状态。
#include<stdio.h>
#include<string.h>
const int maxn=2005,mod=1000000007;
int n,m,ans,now;
int f[2][maxn][11],g[11],h[11];
void solve(int typ){
now=0,f[0][1][1]=1;
if(typ==0)
f[0][2][0]=1;
for(int i=3;i<=n;i++){
now^=1,memset(f[now],0,sizeof(f[now]));
for(int j=1;j<=i;j++){
for(int c=0;c<=10;c++){
g[c]=f[now^1][j][c];
if(typ&&(c==0||c==5||c==8))
g[c]=0;
}
h[0]=h[3]=(0ll+g[0]+g[1]+g[2]+g[8]+g[10])%mod;
h[1]=f[now^1][j][0],h[2]=(g[1]+g[2])%mod;
h[4]=(0ll+g[3]+g[4]+g[5]+g[7])%mod;
h[5]=(0ll+g[4]+g[5]+g[7])%mod;
h[6]=f[now^1][j][5],h[7]=(g[6]+g[7])%mod;
h[8]=g[3];
h[9]=f[now^1][j][8],h[10]=(g[9]+g[10])%mod;
for(int c=0;c<=10;c++){
int nxt=j+(c==0||c==5||c==8);
f[now][nxt][c]=(f[now][nxt][c]+h[c])%mod,h[c]=0;
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
solve(0);
for(int i=m+1;i<=n;i++)
for(int c=0;c<=10;c++)
if(c!=6&&c!=9)
ans=(ans+f[now][i][c])%mod;
memset(f,0,sizeof(f));
solve(1);
for(int c=0;c<=10;c++)
if(c!=0&&c!=5&&c!=6&&c!=8&&c!=9)
ans=(ans+f[now][m][c])%mod;
printf("%d",ans);
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 张高兴的大模型开发实战:(一)使用 Selenium 进行网页爬虫
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构