2022-9-11/12 #27 自弹 自唱 自赏 不如自封为王
发现了栀子的一首歌 Go crazy for me,真上头。
昨天有一根木刺扎进了我右手中指,伤口愈合后挑不出来了,写代码按到那里就会痛一下。
匈牙利跑二分图匹配可以找到增广路后再清空 vis 数组,某些题中会有优越性。(反正不劣)
做了 CF848D Shake It!,觉得挺简单,就不记录了。
CF1726G A Certain Magical Party,sb 结论题,还不会做。
074 CF1292F Nora's Toy Boxes
称数列中没有其真因子的数为好数,调整可知每次使用的 \(a_i\) 都可以是好数。
我们可以丢掉 \(>\lfloor\frac m2\rfloor\) 的好数,于是有用的好数不会超过 \(\lfloor\frac m4\rfloor\) 个,可以状压。
具体地,我们可以将好数分成若干个互不影响的集合再乘上归并的系数,现只考虑一个内部有影响的好数集合。更严谨的说法是,将好数与其倍数连边生成一个二分图,我们分连通块考虑。
可以发现这个连通块最多删右部点数量减一个数,同时这也可以达到。于是我们只需求“初始右部只有一个点激活,按照规则激活右部所有点的方案数”。
对左部点状压,一个直觉的 dp 是 \(f_{S,i}\) 表示左部集合为 \(S\),右部选了 \(i\) 个点的方案数,复杂度 \(O(2^\frac{m}{4}n^2)\),已经可以通过。
类似 AT5042 Edge Ordering,我们可以将状态去除第二维,将其改为“左部集合为 \(S\),且已经计算完仅连向 \(S\) 补集的右部点的贡献”,每次删除一个数也是归并的形式,可以直接计算。
复杂度 \(O(2^\frac m4n^2)\)。
#include<stdio.h>
#include<assert.h>
const int maxn=65,mod=1000000007,maxt=1<<15;
int n,ans,ids,sum;
int a[maxn],gd[maxn],fac[maxn],nfac[maxn],S[maxn],id[maxn],T[maxt],dsu[maxn],g[maxn],f[maxt],h[maxn];
int find(int x){
return dsu[x]==x? x:dsu[x]=find(dsu[x]);
}
int ksm(int a,int b){
int res=1;
while(b){
if(b&1)
res=1ll*res*a%mod;
a=1ll*a*a%mod,b>>=1;
}
return res;
}
int main(){
fac[0]=nfac[0]=1;
for(int i=1;i<=60;i++)
fac[i]=1ll*fac[i-1]*i%mod,nfac[i]=ksm(fac[i],mod-2);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),dsu[i]=i;
for(int i=1;i<=n;i++){
gd[i]=a[i]<=30;
for(int j=1;j<=n;j++)
gd[i]&=(i==j||a[i]%a[j]!=0);
if(gd[i]){
id[i]=++ids;
for(int j=1;j<=n;j++)
if(i!=j&&a[j]%a[i]==0)
S[j]|=(1<<(ids-1)),dsu[find(j)]=find(i);
}
}
ans=1;
for(int t=1;t<=n;t++)
if(dsu[t]==t){
int c=0,s=0,cnt=0;
for(int i=1;i<=n;i++)
if(find(i)==t){
if(gd[i])
g[++c]=i,s|=g[c];
else h[++cnt]=i;
}
if(s==0||cnt==0)
continue;
for(int i=1;i<=cnt;i++){
S[i]=0;
for(int j=1;j<=c;j++)
if(a[h[i]]%a[g[j]]==0)
S[i]|=(1<<(j-1));
T[S[i]]++;
}
for(int i=0;i<c;i++)
for(int j=0;j<(1<<c);j++)
if((j>>i)&1)
T[j]+=T[j^(1<<i)];
f[(1<<c)-1]=1;
for(int i=(1<<c)-2;i>=0;i--){
for(int j=1;j<=cnt;j++)
if(i==0||(i&S[j])>0){
int nxt=i|S[j];
if(nxt>i)
f[i]=(f[i]+1ll*f[nxt]*fac[cnt-T[i]-1]%mod*nfac[cnt-T[nxt]])%mod;
}
}
ans=1ll*ans*nfac[cnt-1]%mod*f[0]%mod,sum+=cnt-1;
for(int i=0;i<(1<<c);i++)
f[i]=T[i]=0;
}
printf("%d\n",(int)(1ll*fac[sum]*ans%mod));
return 0;
}
075 CF722E Research Rover
我真 sb。
一眼可以看出一个 dp,令 \(f_{x,i}\) 表示到达 \(x\),恰好经过 \(i\) 个关键点的方案数,将点按照 \(x,y\) 双关键字排序后暴力转移即可,第二维显然是 \(\log\) 的。
但是会算重,一开始的想法是转钦定,先不论能不能计数钦定,由于钦定要转回来,我们第二维就不能缩小为 \(\log\) 了。
但是可以在转移过程中去重,转移完一个点差分一下就好了。。。(可以发现转移后的 \(f_{x,i}\) 表示至少 \(i\) 个关键点的方案数,因为每一条这样的路径都会且仅会在第 \(i\) 个关键点对 dp 值产生贡献)
复杂度 \(O(n^2\log V)\)。
#include<stdio.h>
#include<algorithm>
using namespace std;
const int maxn=2005,maxN=200005,maxk=25,mod=1000000007;
int n,m,k,s,ans;
int fac[maxN],nfac[maxN],inv[maxN],f[maxn][maxk],g[maxk],x[maxn],y[maxn];
struct point{
int x,y;
}p[maxn];
inline int cmp(point a,point b){
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
inline int w(int a,int b){
return 1ll*fac[a+b]*nfac[a]%mod*nfac[b]%mod;
}
int main(){
fac[0]=fac[1]=nfac[0]=nfac[1]=inv[1]=1;
for(int i=2;i<=200000;i++)
fac[i]=1ll*fac[i-1]*i%mod,inv[i]=mod-1ll*(mod/i)*inv[mod%i]%mod,nfac[i]=1ll*nfac[i-1]*inv[i]%mod;
scanf("%d%d%d%d",&n,&m,&k,&s);
for(int i=1;i<=k;i++)
scanf("%d%d",&p[i].x,&p[i].y);
sort(p+1,p+1+k,cmp);
if(p[k].x!=n||p[k].y!=m)
p[++k]=point{n,m};
else s=(s+1)/2;
if(p[1].x!=1||p[1].y!=1)
p[++k]=point{1,1};
else s=(s+1)/2;
if(k==1){
printf("%d\n",s);
return 0;
}
sort(p+1,p+1+k,cmp);
for(int i=1;i<=k;i++)
x[i]=p[i].x,y[i]=p[i].y;
f[1][0]=1;
for(int i=2;i<=k;i++){
for(int p=1;p<i;p++)
if(x[i]>=x[p]&&y[i]>=y[p]){
int v=w(x[i]-x[p],y[i]-y[p]);
for(int j=0;j<=24;j++)
if(f[p][j]){
int nxt=min(j+1,24);
g[nxt]=(g[nxt]+1ll*f[p][j]*v)%mod;
}
}
for(int j=1;j<=24;j++)
f[i][j]=(g[j]-(j==24? 0:g[j+1])+mod)%mod,g[j]=0;
}
for(int i=1;i<=24;i++)
ans=(ans+1ll*s*f[k][i])%mod,s=(s+1)/2;
printf("%d\n",(int)(1ll*ans*nfac[n+m-2]%mod*fac[n-1]%mod*fac[m-1]%mod));
return 0;
}
076 CF1718D Permutation for Burenka
建出笛卡尔树,可以得知每个位置填的数字的范围,那么判定实际上等价于寻找数字与位置的完美匹配,且数字大小关系服从一个排列。
我们发现服从排列的限制其实是无关紧要的,若不满足则有一对笛卡尔树上存在祖先关系的点 \((x,y)\) 满足 \(a_x<a_y\),此时交换 \(a_x,a_y\) 即可,容易发现一定能交换。
这个问题有一个经典的贪心做法:按照右端点从小到大顺序枚举每个区间 \([l,r]\),取出 \(\leqslant l\) 的最小值,若其 \(\leqslant r\) 则删除这个数,否则不存在完美匹配。
可以通过霍尔定理说明合法的数字一定是一个区间(去除序列中出现的数字),于是我们只需找到其左右端点。
类似上述贪心算法,若找不到数就说明 \(>r\) 的所有数字不合法,判定一下 \(r\) 是否合法就可以得知区间的右端点。
反着做一遍就可以得到左端点了,复杂度 \(O(n\log n)\)。
#include<stdio.h>
#include<set>
#include<map>
#include<algorithm>
using namespace std;
const int maxn=300005;
int T,n,m,k,tot,L,R,top,flg;
int p[maxn],a[maxn],b[maxn],stk[maxn],lc[maxn],rc[maxn],l[maxn],r[maxn],id[maxn];
map<int,int>mp;
set<int>s;
void dfs(int x){
if(lc[x])
r[lc[x]]=min(r[lc[x]],r[x]),dfs(lc[x]),l[x]=max(l[x],l[lc[x]]);
if(rc[x])
r[rc[x]]=min(r[rc[x]],r[x]),dfs(rc[x]),l[x]=max(l[x],l[rc[x]]);
}
inline int cmpR(int a,int b){
return r[a]<r[b]||(r[a]==r[b]&&l[a]<l[b]);
}
inline int cmpL(int a,int b){
return l[a]>l[b]||(l[a]==l[b]&&r[a]>r[b]);
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m),s.clear(),mp.clear(),k=top=flg=L=0,R=1e9;
for(int i=1;i<=n;i++){
scanf("%d",&p[i]);
int k=top;
while(k&&p[stk[k]]<p[i])
k--;
if(k>0)
rc[stk[k]]=i;
if(k<top)
lc[i]=stk[k+1];
top=k,stk[++top]=i;
}
for(int i=1;i<=n;i++){
scanf("%d",&a[i]),mp[a[i]]=1;
if(a[i])
l[i]=r[i]=a[i];
else l[i]=1,r[i]=1e6,id[++k]=i;
}
dfs(stk[1]);
for(int i=1;i<k;i++)
scanf("%d",&b[i]),s.insert(b[i]);
for(int i=1;i<=n;i++)
flg|=(l[i]>r[i]);
sort(id+1,id+k+1,cmpR);
for(int i=1;i<=k;i++){
int x=l[id[i]],y=r[id[i]];
set<int>::iterator it=s.lower_bound(x);
if(it==s.end()||*it>y){
if(R==1e9)
R=y;
else flg=1;
}
else s.erase(it);
}
s.clear();
for(int i=1;i<k;i++)
s.insert(b[i]);
sort(id+1,id+k+1,cmpL);
for(int i=1;i<=k;i++){
int x=l[id[i]],y=r[id[i]];
set<int>::iterator it=s.upper_bound(y);
int c=it==s.begin();
if(c==0)
it--,c=*it<x;
if(c){
if(L==0)
L=x;
else flg=1;
}
else s.erase(it);
}
if(flg)
L=1,R=0;
for(int i=1,x;i<=m;i++)
scanf("%d",&x),puts(mp.count(x)==0&&x>=L&&x<=R? "YES":"NO");
for(int i=1;i<=n;i++)
lc[i]=rc[i]=0;
}
return 0;
}
077 ARC128F Game against Robot
令 \(n\leftarrow \frac n2\)
类似 UNR D1T3 稳健型选手,我们可以得到排列确定时的策略:
按照 \(p_i\) 大小从大到小排序,每次加入两个数字到堆中,然后取出堆中最大值。
考虑每个数字的贡献,我们就可以将数字分成 \(\geqslant x\) 与 \(<x\) 的两部分,那么就可以把序列改写成 01 序列,堆的变化就很好刻画了,容易得到一个 \(O(n^3)\) 或 \(O(n^2)\) 的 dp。
这样仍然不好考虑,因为我们在考虑的数字和 \(\geqslant x\) 的数字是不同的。一种更好的方式是考虑 \(\geqslant x\) 的数字,计算这些数字被删除的次数之和,最后乘上 \(m!(2n-m)!\)。
将堆的变化看作格路行走,那么就是从 \(x=0\) 走到 \(x=n\),每次向右走一步,然后要么向上走一步,要么向下走一步,要么 \(y\) 不变(此时有两种方案),最后将 \(y\) 对 \(0\) 取 \(\max\)。
偷一张图:(来自 苹果蓝17)
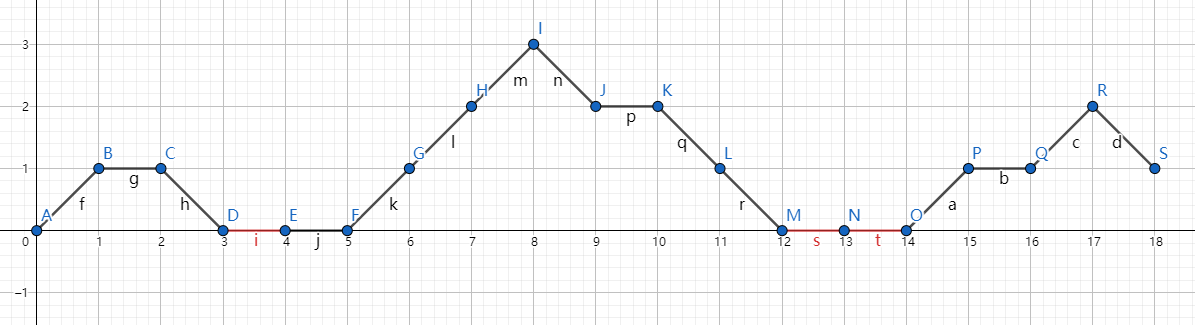
可以发现红边数量即弹出 \(0\) 的数量,我们只需计数红边数量。
若我们去除将 \(y\) 对 \(0\) 取 \(\max\) 操作(这样格路的终点也能确定下来,是 \((n,m-n)\)),观察可知对应格路的最低点距离 \(x\) 轴的距离就是红边数量,于是我们枚举最低点:
先考虑一个简单一点的问题:按照上面的行走规则,从 \((0,0)\) 走到 \((n,m)\) 的方案数。
最低点距离 \(x\) 轴距离等于 \(k\) 不好算,但是其越过 \(y=k\) 的方案数是经典的折线法问题,答案是 \({2n\choose (m-n)+n}-{2n\choose (2(k-1)-(m-n))+n}={2n\choose m}-{2n\choose m-2k+2}\)。
那么恰好为 \(k\) 的方案数就是 \({2n\choose m-2k}-{2n\choose m-2k+2}\)。
于是可以列出答案的式子:(令 \(t=\max(0,m-n)\))
复杂度 \(O(n)\)。
#include<stdio.h>
#include<algorithm>
using namespace std;
const int maxn=1000005,mod=998244353;
int n,ans;
int f[maxn],fac[maxn],nfac[maxn],inv[maxn],a[maxn],all[2],pre[maxn];
int C(int a,int b){
return a<b? 0:1ll*fac[a]*nfac[b]%mod*nfac[a-b]%mod;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+1+n);
fac[0]=fac[1]=nfac[0]=nfac[1]=inv[1]=1;
for(int i=2;i<=n;i++)
fac[i]=1ll*fac[i-1]*i%mod,inv[i]=mod-1ll*(mod/i)*inv[mod%i]%mod,nfac[i]=1ll*nfac[i-1]*inv[i]%mod;
pre[0]=1,pre[1]=n;
for(int i=2;i<=n;i++)
pre[i]=(pre[i-2]+C(n,i))%mod;
all[0]=pre[n],all[1]=pre[n-1];
for(int m=0;m<=n;m++){
int k=max(0,n/2-m);
f[m]=(1ll*(0ll+n/2-k+mod)*C(n,m+k+k)-(m+k+k>n? 0:(all[m&1]-pre[m+k+k]+mod))+mod)%mod*fac[m]%mod*fac[n-m]%mod;
}
for(int i=1;i<=n;i++)
ans=(ans+1ll*(f[i]-f[i-1]+mod)*a[n-i+1])%mod;
printf("%d\n",ans);
return 0;
}


