AGC039D Incenters 解题报告
AGC039D Incenters 解题报告:
题意
给定单位圆上 \(n\) 个点,随机选三个点求三角形内心期望。
\(3\leqslant n\leqslant 3000\)。
分析
不会推式子/dk。
首先作出三个角的角平分线,连接角平分线与单位圆交的三个点,那么这个新三角形的垂心等于原三角形的重心。
证明就是 \(\angle CDF+\angle AFE+\angle AFD=\angle CAF+\angle ABE+\angle ACD=\frac{\angle BAC+\angle ABC+\angle ACB}{2}=90^{\circ}\)。(其他角类似)
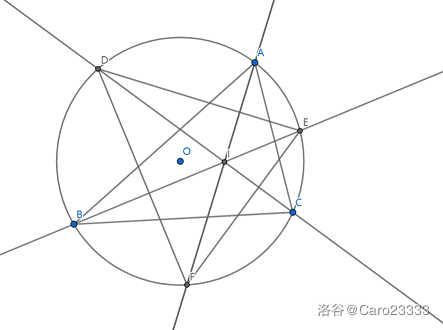
(蒯了几张图,from Caro23333)
然后作出欧拉线,令 \(O,G,H\) 分别为外心、重心、垂心,有 \(GH=2OG\)。
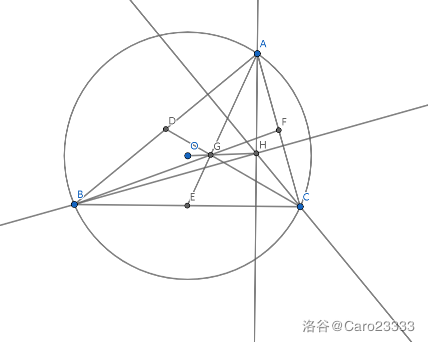
而外心就是原点,因此 \(H_x=3G_x=D_x+E_x+F_x\),也就是说我们要求三个弧中点 \(x\) 坐标和的期望。
然后就是推式子了:
令 \(C=\frac{n(n-1)(n-2)}{6}\) 为总方案数。
\[\text{E}(H_x)\times C=\sum_{i=1}^n\sum_{j=i+1}^n\sum_{k=j+1}^n(\cos\frac{\pi(A_i+A_j)}{L}-\cos\frac{\pi(A_i+A_k)}{L}+\cos\frac{\pi(A_j+A_k)}{L})\\=\sum_{i=1}^n\sum_{j=i+1}^{n}(n-2-2(j-i-1))\cos\frac{\pi(A_i+A_j)}{L}\\=\sum_{i=1}^n\sum_{j=i+1}^n(n+2i-2j)(\cos a_i\cos a_j-\sin a_i\sin a_j)\\=\sum_{i=1}^n(((n+2i)\sum_{j=i+1}^n\cos a_j-\sum_{j=i+1}^n 2j\cos a_j)\cos a_i-((n+2i)\sum_{j=i+1}^n \sin a_j-\sum_{j=i+1}^n 2j\sin a_j)\sin a_i)
\]
同理可以推出 \(H_y\),这里就写一下结果:
\[\text{E}(H_y)\times C=\sum_{i=1}^n(((n+2i)\sum_{j=i+1}^n\cos a_j-\sum_{j=i+1}^n 2j\cos a_j)\sin a_i-((n+2i)\sum_{j=i+1}^n \sin a_j-\sum_{j=i+1}^n 2j\sin a_j)\cos a_i)
\]
时间复杂度 \(O(n)\)。
代码
#include<stdio.h>
#include<math.h>
const int maxn=3005;
const double pi=acos(-1.0);
int n,L;
int a[maxn];
double ansx,ansy,C,sc,sci,ss,ssi;
int main(){
scanf("%d%d",&n,&L);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=n;i>=1;i--){
double A=1.0*a[i]*pi/L,ca=cos(A),sa=sin(A),vc=(1.0*(n+i+i)*sc-2*sci),vs=(1.0*(n+i+i)*ss-2*ssi);
ansx+=vc*ca-vs*sa,ansy+=vc*sa+vs*ca,sc+=ca,sci+=ca*i,ss+=sa,ssi+=sa*i;
}
double C=1.0*n*(n-1)*(n-2)/6;
printf("%.15lf %.15lf\n",ansx/C,ansy/C);
return 0;
}


