快速排序

快速排序

主要思想

快速排序所采用的思想是分治的思想。所谓分治，就是指以一个数为基准，将序列中的其他数往它两边“扔”。以从小到大排序为例，比它小的都“扔”到它的左边，比它大的都“扔”到它的右边，然后左右两边再分别重复这个操作，不停地分，直至分到每一个分区的基准数的左边或者右边都只剩一个数为止。这时排序也就完成了。

流程

• 确定基准值\(x\)，选择的方式一般有三种：左端点 右端点 中间点

  基准值的选择不同也会导致代码的运行时长不同，一般来说都取中间点

• 调整区间，使左半边全部 \(\leq x\)，右半边全部 \(\geq x\)

• 按照以上两个步骤递归处理两端，直到区间里只剩下一个元素

具体实现

朴素做法

• 开两个数组，\(a\)和\(b\)，再开一个数组\(q\)用来存储答案
• 定义一个函数用来处理数组，需要两个参数\(l\)和\(r\)，表示左端点和右端点，从\(l\)遍历到\(r\)
• 分情况处理：
  • \(q_i\leq x\) 将\(q_i\)放到\(a\)数组中
  • \(q_i\geq x\) 将\(q_i\)放到\(b\)数组中
• 重复2 3 两步操作，直到区间里只剩下一个元素，即 \(l\geq r\)
• 最后合并两个数组

优化思路

按照以上方法，我们将会浪费很多空间，那么如何在不另外开辟空间的情况下完成任务呢？

我们可以借鉴双指针的思路，为了好听我们将两个指针命名为 “哨兵”

我们先来回顾一下，双指针的主要用途是什么？ 主要是用来维护一段区间

于是我们可以用 \(i\) 来维护左区间，使得 \(i\) 左边的数都 \(\leq x\)，用 \(j\) 来维护右区间，使得 \(j\) 右边的数都 \(\geq x\)

优化做法

• 定义两个“哨兵” \(i\) 和 \(j\)，开始时指向区间的左右两端
• 当 \(i\) 指向的数 \(<x\) 时，就往右移动，直到指向的数 \(\geq x\)
• 当 \(j\) 指向的数 \(> x\) 时，就往左移动，直到指向的数 \(\leq x\)
• 当 \(i\) 和 \(j\) 的移动停止时，交换 \(i\) 和 \(j\) 指向的数，\(i\) 往右移动一个，\(j\) 往左移动一个

一直重复以上的步骤，直到两个哨兵相遇为止，即当 \(i\geq j\) 时

样例模拟

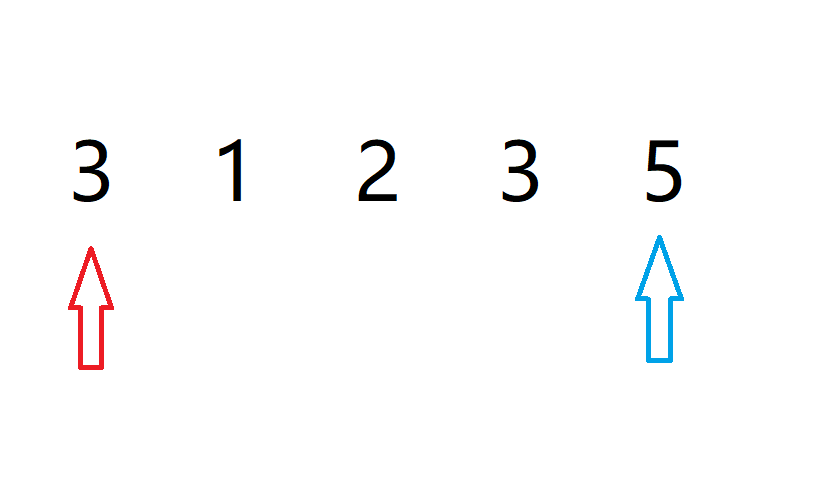
注意点

快排与二分的注意点是一样的，都是边界问题

在递归分别处理时容易出现这个问题

• 当分界点取 \(i-1\) 和 \(i\) 时，分界点不能取 \(l\)，要取 \((l+r+1)/2\)，注意上取整
• 当分界点取 \(j\) 和 \(j+1\) 时，分界点不能取 \(r\)，要取 \((l+r)/2\)，区别于上一种

算法分析

时间复杂度 \(O(nlogn)\)

快速排序是不稳定的

何为稳定性？

当排序时如果遇到两个数值相同，一般来说把靠前的那个往后移

换句话来说就是排完序后，两个相同的数的相对位置不发生变化

而快速排序无法保证这一点，所以不稳定

如何解决？
我们可以用stl里的map保存下标，使得每一个数具有唯一性

代码模板

#include <iostream>
using namespace std;
int q[100000] = { 0 };
int n;
void quicksort(int q[], int l, int r)
{
	if (l >= r)return;
	int i = l - 1, j = r + 1, x = q[l + r >> 1];
	while (i < j)
	{
		do i++; while (q[i] < x);
		do j--; while (q[j] > x);
		if (i < j)swap(q[i], q[j]);
	}
	quicksort(q, l, j), quicksort(q, j + 1, r);
}

int main()
{
	scanf("%d", &n);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &q[i]);
	}
	quicksort(q, 0, n-1);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", q[i]);
	}
	return 0;
}