数据结构之图
前言
1.图状结构是我们研究的结构里面最复杂的结构
2.图的相关关系非常复杂,相关概念非常多
但是图又很重要,不管是地图,人物关系等,把每个人或者每个地方看作一个点,其他的点都会与之有上千万的联系。所有就都有及其复杂的网络,不管是路径规划,导航提醒还是警察在断案,其实本质上都是图的应用。
图的定义
图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的;其中,点通常称为顶点(vertex),而点到点之间的连线通常称之为边或者弧(edge)。通常记为G=(V,E)。
注意:线性表可以是空表,树可以是空树,图不可以是空图,图可以没有边,但是至少要有一个顶点。
- 线性表中我们把数据元素叫元素,树中将数据元素叫结点,在图中数据元素,我们则称之为顶点(Vertex)。
- 线性表中可以没有数据元素,称为空表。树中可以没有结点,叫做空树。
- 线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,而图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
1.无向图
如果一个图结构中,所有的边都没有方向性,那么这种图便称为无向图。典型的无向图,如图二所示。由于无向图中的边没有方向性,这样我们在表示边的时候对两个顶点的顺序没有要求。例如顶点VI和顶点V5之间的边,可以表示为(V2, V6),也可以表示为(V6,V2)。
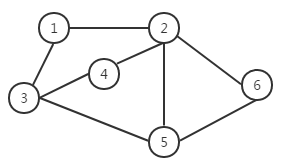
图二 无向图
对于图二无向图,对应的顶点集合和边集合如下:
V(G)= {V1,V2,V3,V4,V5,V6}
E(G)= {(V1,V2),(V1,V3),(V2,V6),(V2,V5),(V2,V4),(V4,V3),(V3,V5),(V5,V6)}
2.有向图
一个图结构中,边是有方向性的,那么这种图就称为有向图,如图三所示。由于图的边有方向性,我们在表示边的时候对两个顶点的顺序就有要求。我们采用尖括号表示有向边,例如<V2,V6>表示从顶点V2到顶点V6,而<V6,V2>表示顶点V6到顶点V2。
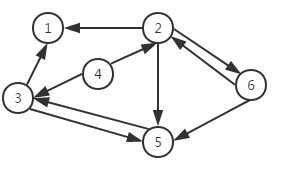
图三 有向图
对于图三有向图,对应的顶点集合和边集合如下:
V(G)= {V1,V2,V3,V4,V5,V6}
E(G)= {<V2,V1>,<V3,V1>,<V4,V3>,<V4,V2>,<V3,V5>,<V5,V3>,<V2,V5>,<V6,V5>,<V2,V6>,<V6,V2>}
有权图和无权图
所谓有权图就是每条边都具有一定的权重,通常就是边上的那个数字;而无权图就是每条边没有权重。 如下图所示即为有权图,(A,B)的权就是13。
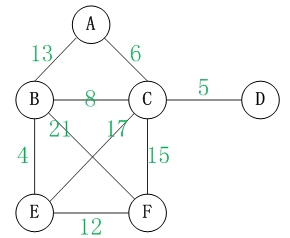
连通、连通图、连通分量
在无向图中,两顶点有路径存在,就称为连通的。若图中任意两顶点都连通,同此图为连通图。无向图中的极大连通子图称为连通分量。
以下面两个图为例,下面的图是上面的图的连通分量,并且下面的图是连通图。上面图中I与J也是连通的。
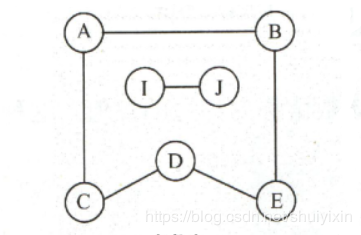
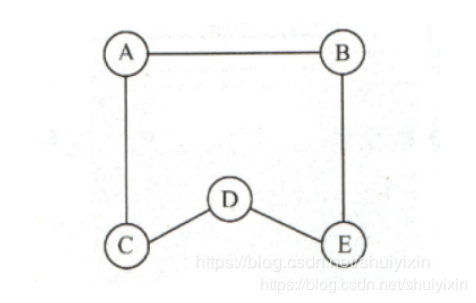
上图的一个连通分量
强连通图、强连通分量
在有向图中,两顶点两个方向都有路径,两顶点称为强连通。若任一顶点都是强连通的,称为强连通。有向图中极大强连通子图为有向图的强连通分量。
以下面的图为例:下图就是一个强连通图,并且是下面图的强连通分量。
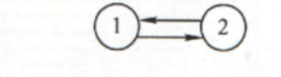
![]()
顶点的度、入度和出度
顶点的度为以该顶点为一个端点的边的数目。
对于无向图,顶点的边数为度,度数之和是顶点边数的两倍。
对于有向图,入度是以顶点为终点,出度相反。有向图的全部顶点入度之和等于出度之和且等于边数。顶点的度等于入度与出度之和。
注意:入度与出度是针对有向图来说的。
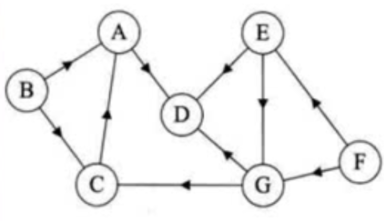
A出度:1 A入度:2
图的存储
邻接矩阵
邻接矩阵是一个二维数组,数据项表示两点间是否存在边,如果图中有 N 个顶点,邻接矩阵就是 N*N 的数组。
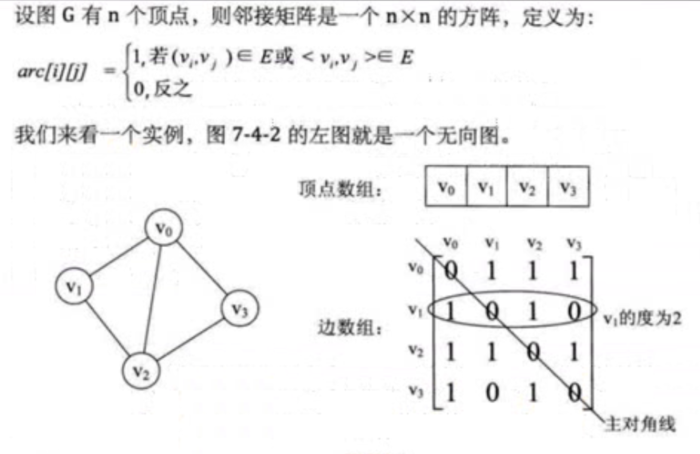
无向图的边数组是一个对称矩阵
1表示有边,0表示没有边,顶点与自身相连用 0 表示
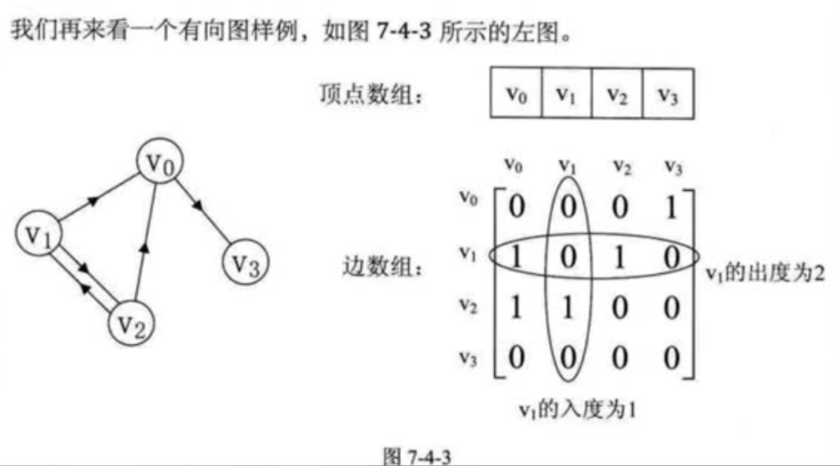
横向为:出度 纵向为:入度
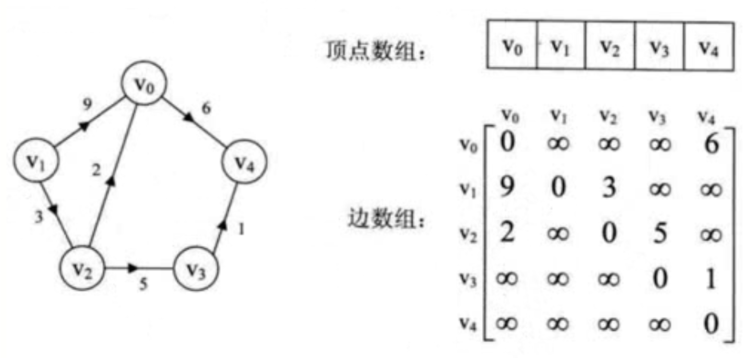
不要混淆度和权值!! V2的入度为:1 V2的入度权值为:3
邻接表
邻接表是一个链表数组(或者是链表的链表),每个单独的链表表示了有哪些顶点与当前顶点邻接。
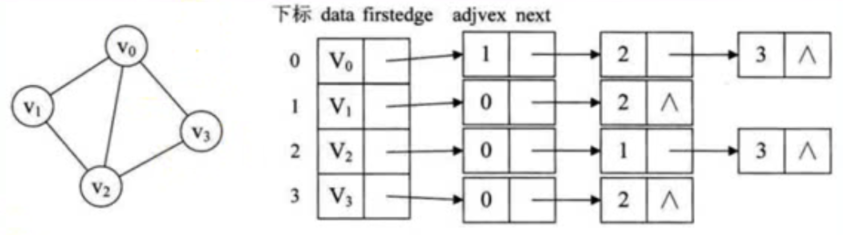
无向图的邻接表(指的边数)
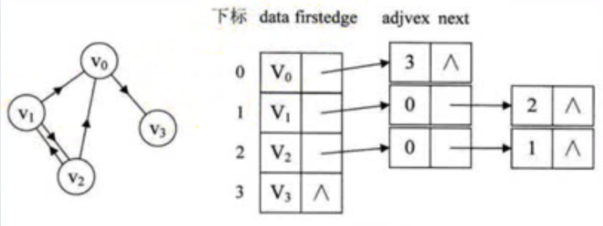
有向图的邻接表(指的出度)
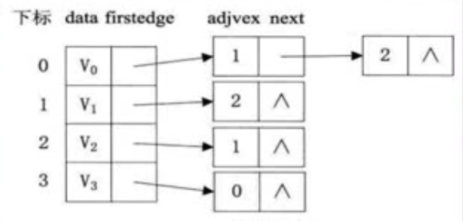
有向图的逆邻接表(指的入度)
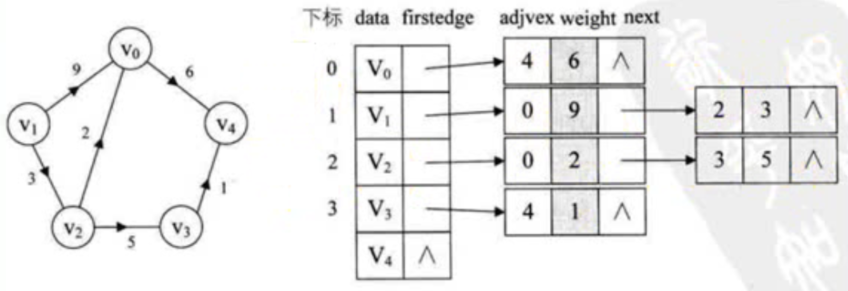
带权值邻接表(指的出度)


