数据结构与算法 - 栈和队列
栈(stack)
先进后出,删除与加入均在栈顶操作
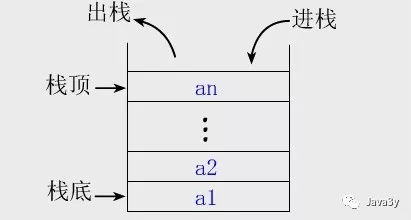
栈也称为堆栈,是一种线性表。
堆栈的特性: 最先放入堆栈中的内容最后被拿出来,最后放入堆栈中的内容最先被拿出来, 被称为先进后出、后进先出。
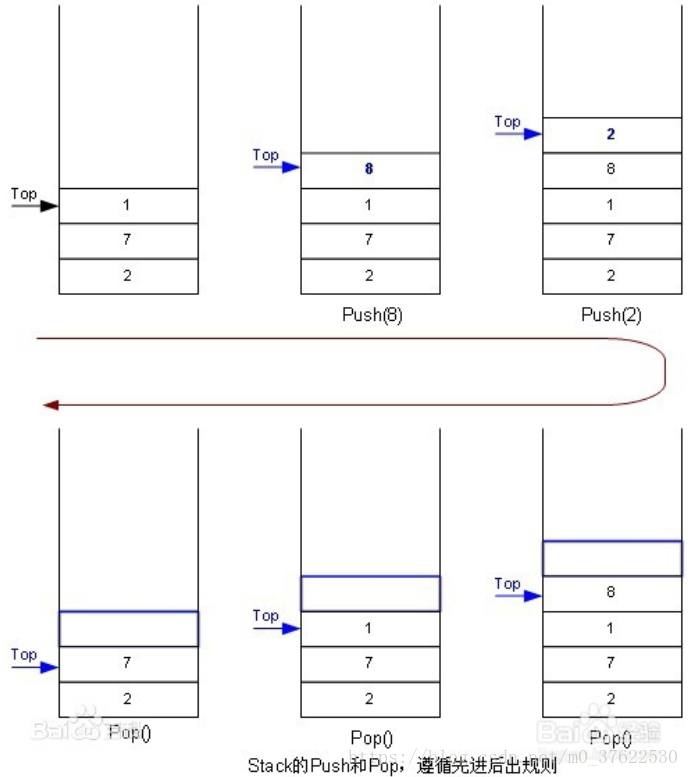
堆栈中两个最重要的操作是PUSH和POP,两个是相反的操作。
PUSH:在堆栈的顶部加入一 个元素。
POP:在堆栈顶部移去一个元素, 并将堆栈的大小减一。
在成员变量方面,Vector提供了elementData , elementCount, capacityIncrement三个成员变量。其中
elementData :"Object[]类型的数组",它保存了Vector中的元素,可以随着元素的增加而动态的增长,如果在初始化Vector时没有指定容器大小,则使用默认大小为10.
private static final int DEFAULT_SIZE = 10;初始化的值
protected int elementCount; 栈元素数量(非空元素的长度)
/**
* 使用指定的初始容量和容量增量构造一个空的向量。
*/
public Vector(int initialCapacity, int capacityIncrement) { //初始化
super();
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal Capacity: "+initialCapacity);
this.elementData = new Object[initialCapacity];
this.capacityIncrement = capacityIncrement;
}
protected int capacityIncrement;扩容增长因子向量的大小大于其容量时,容量自动增加的量。
如果在创建Vector时,指定了capacityIncrement的大小;则,每次当Vector中动态数组容量增加时>,增加的大小都是capacityIncrement。
如果容量的增量小于等于零,则每次需要增大容量时,向量的容量将增大一倍。
容量是最多能够容纳多少元素,而大小是目前容纳了多少元素
得到最后元素的下标
public synchronized E peek(){
try{
return(E)elementData[elementCount-1]; //当前数组[当前数组长度-1] >>得到最后元素的下标
}catch(IndexoutOfBoundsException e){
throw new EmptyStackException(); //得到下标,肯定会抛出异常
}}
出栈
@Suppres swarnings("unchecked")
public synchronized E pop(){
if(slementCount==0){ //栈元素数量为0,表示空栈
throw new EmptyStackException(); //空栈异常
}
final int index = --elementCount; //将来要出栈的非空元素下标,栈数量-1就是下标
栈数量:1 2 3 4
下标:0 1 2 3
final E obj=(E)elementData[index]; //拿到栈顶元素,让它等于obj
elementData[index]=nul1;把栈顶变成null,下次再出栈,非空元素长度减一得到下标,又是有数据的了
modCount++; //发生改变,进行加一操作
return obj;
}
入栈
public synchronized void addElement(E object){
if(elementCount==elementData.1ength){//判断是否栈满
growByOne(); //栈满,扩容一次,长度不定
}
elementData[ elementCount++]=object;
modCount++;
}
private void growByOne(){
int adding=0; //要添加的数量
if(capacityIncrelent <=0){
if((adding=elementData.length)==0){ //如果是空栈,要添加元素的话,让adding=1,增加一个元素 存疑?
adding=1;
} else{
adding = capacityIncrement; //capacityIncrement用它来判断需要扩容多少
}
E[] newData=newElementArray(elementData. length +adding);//新创建一个数组,把它的长度扩容成 增加的长度+扩容的
System. arraycopy(elementData,0, newData,0, elementCount);//拷贝数据
elementData=newData;
}
为什么每个方法里都要有全局变量和局部变量
安全问题:因为elementData可以会进行入栈和出栈操作,如果直接使用elementData,不能进行边遍历边删除,所以要使用局部变量Object[] dumpArray
栈里面可以有重复的元素
栈的遍历可以从栈顶也可以从栈底,这个需要根据自己需求,为自己服务
栈的经典应用
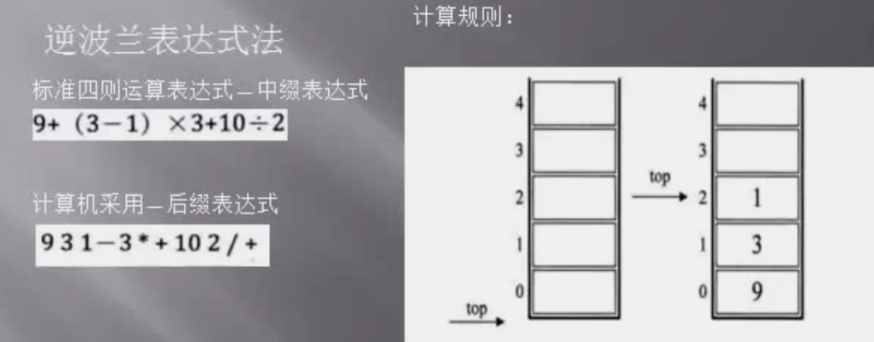
后缀表达式
931 - 3 * + 10 2 / +
923 * + 10 2 / +
96 + 10 2 / +
15 10 2 / +
15 5 +
20
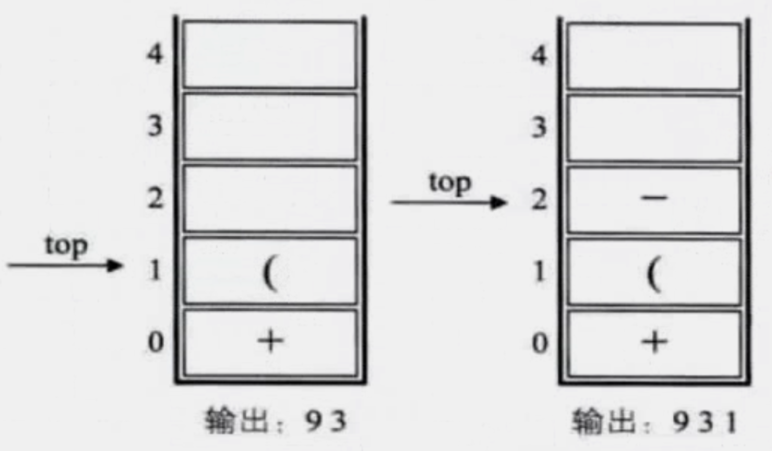
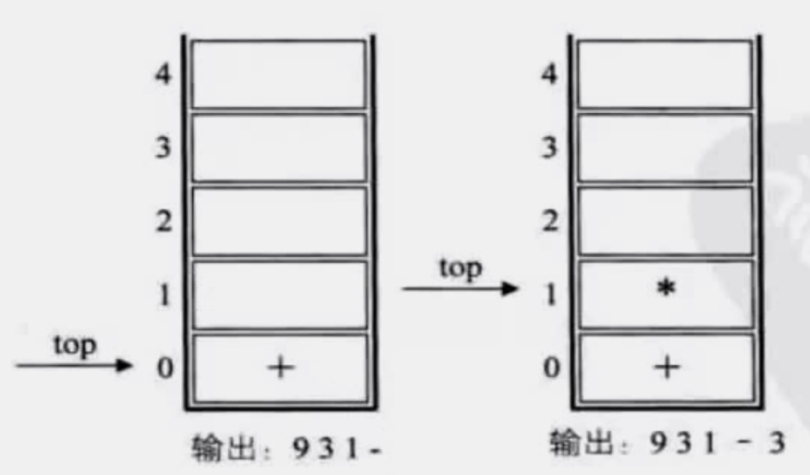
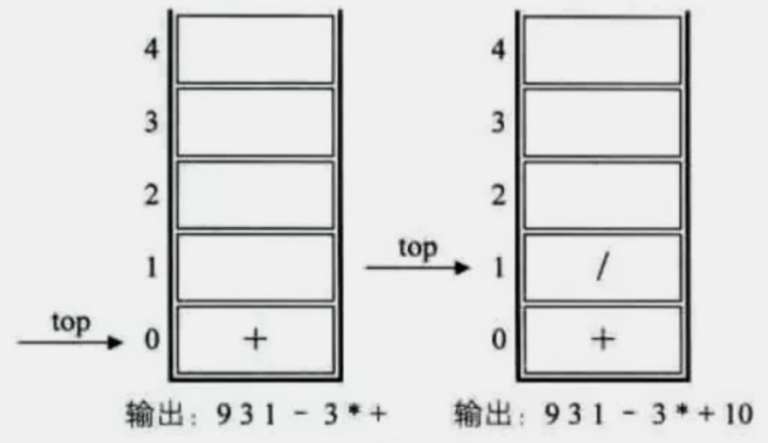
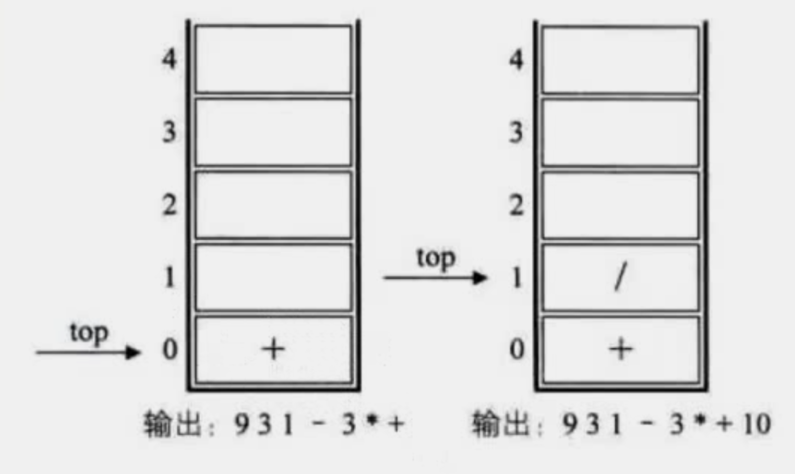
中缀表达式 转 后缀表达式: 数字输出,运算符进栈,括号匹配出栈,栈顶优先级低出栈(精髓就是优先级越高越靠前)
9 + (3 - 1) × 3 + 10 ÷ 2 >> 931 - 3 * + 10 2 / +

队列
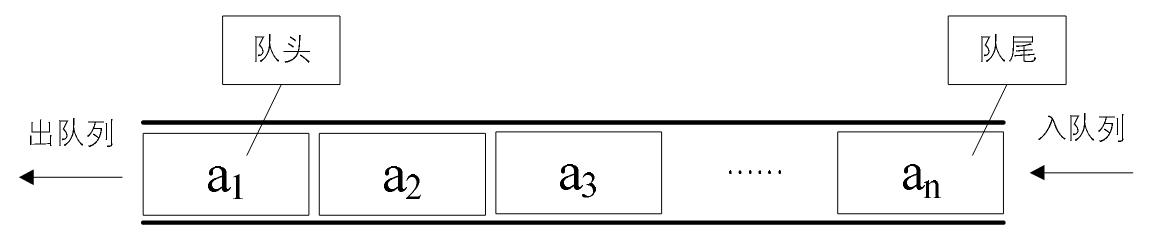
相对于栈而言,队列的特性是:先进先出
-
先排队的小朋友肯定能先打到饭!
队列的顺序存储

缺点:出队复杂度高0(n)
容易假溢出
容易造成资源浪费
队列的链式存储及结构模式
队列的链式存储结构,其实就是线性表的单链表,只不过它只能尾进头出而已
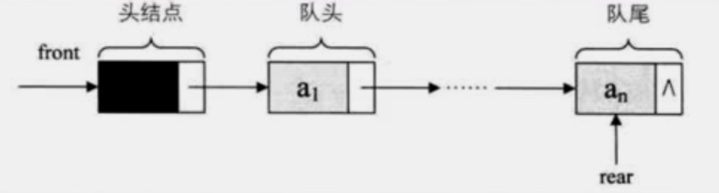
出队:只需要让头指针指向a2,a1就出队了
入队:只需要让尾指针指向新结点,让an的next结点指向新进来的结点
队列也分成两种:
-
静态队列(数组实现)
-
动态队列(链表实现)
值得注意的是:往往实现静态队列,我们都是做成循环队列
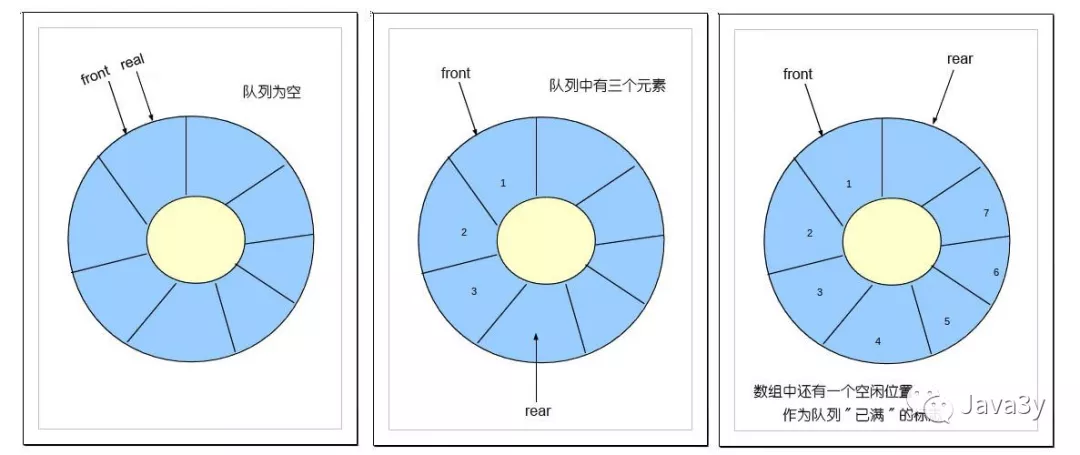
做成循环队列的好处是不浪费内存资源!
类到底采用什么样的数据结构
transient Link<E>voidLink;头指针
public Linkedlist(){初始化 voidLink=new Link<E>(null, null, null); 创建
voidLink. previous = voidLink;
voidLink. next = voidLink; //前后指针都指向自己(自己抱着自己),后面进来的数据到底采用什么样的数据结构要看add方法
队列随机位置插入
public void add (int location, E object){
二分法查找
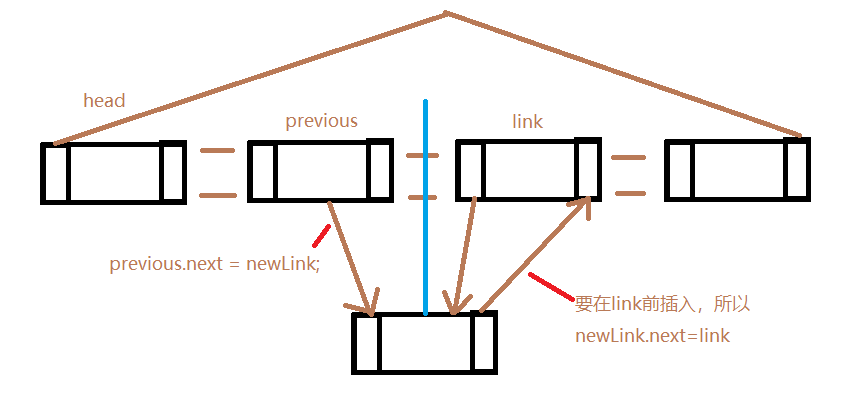
link就是准备在这个位置插入一个新结点进来,当前结点
Link<E> previous = link.previous;
Link<E> newLink = new Link<E>(object,previous(previous),link(next));//新结点
previous.next = newLink;
link.previous = newLink;
}
入队(只有队头的情况下)
private boolean addlastImpl(E object){ Link<E>oldLast=voidLink. previous; //在没有任何元素的情况下,void.link.previous等于它自己,也就是oldLast为head
Link<E> newlink =new Link<E>(object, oldLast(previous指向head), voidlink(next也指向head));
voidLink. previous =newlink;
oldLast.next=newlink;
size++;
modCount++;
return true;
}
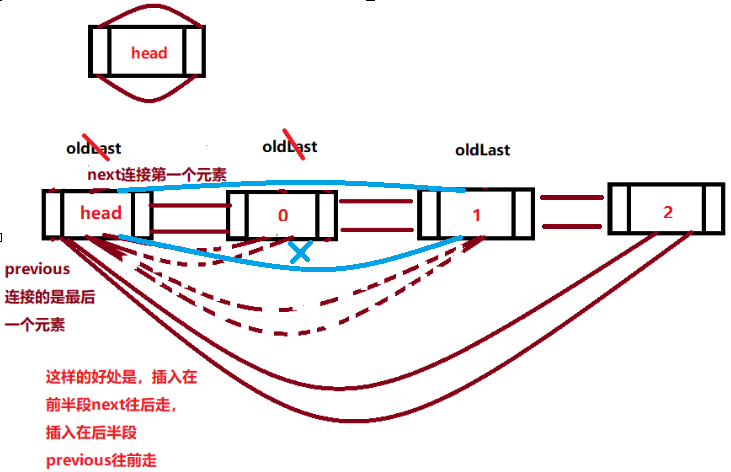
本身就是一个循环,头尾可以选择,然后按照自己的选择写数据结构
出队
voidlink = head
first = 0
next = 1
privateE removeFirstImpl(){
Link<E>first = voidLink. next; //头指针指向了第一个元素=first
if(first = voidlink){ //如果first不等于voidlink,说明是有元素的
Link<E>next = first.next; //让1=next,然后first.next指向它
voidLink.next = next;
next. previous = voidLink;
size--;
modCount++;
return first.data;
}
throw new NoSuchElementException();
}

