数据结构与算法 - 线性表
什么是数据结构?
♦ ♦ 讲的还是数据之间的关系,简单地说,数据结构是以某种特定的布局方式存储数据的容器。这种“布局方式”决定了数据结构对于某些操作是高效的,而对于其他操作则是低效的。
①《数据结构与算法分析》一书中的定义是:“数据结构是 ADT(抽象数据类型Abstract Data Type) 的物理实现。”
② 数据结构包括数据对象集以及它们在计算机中的组织方式,即它们的逻辑结构和物理存储结构,同时还包括与数据对象集相关的操作集,以及实现这些操作的最高效的算法。
③ 个人:就是把图书馆中的书转化为一些字符数据存入电脑中,以及对这些数据对象集的操作。如找书,摆放、放书等。
逻辑结构:数据的逻辑结构就是数据之间关系,如顺序关系,隶属关系等
抽象数据类型:又叫引用数据类型,泛指除基本数据类型以外的数据类型,可以实例化的,具有属性和方法。
抽象数据类型是由若干基本数据类型归并之后形成的一种新的数据类型,这种类型由用户定义,功能操作比基本数据类型更多,一般包括结构体和类。其实说白了,抽象数据类型就是把一些有一定关联的基本数据类型打包,然后当做新的数据类型使用。其实实体类也是,可以调用其中的setter,getter方法。
什么是算法?
算法是在有限步骤内求解某一问题所使用的一组定义明确的规则。
通俗点说,就是计算机解题的过程。 在这个过程中,无论是形成解题思路还是编写程序,都是在实施某种算法。 前者是推理实现的算法,后者是操作实现的算法。
数据结构关算法什么事?
例一: 计算机对弈(下五子棋)
算法:?对弈的规则和策略
模型(数据结构):?棋盘棋子的表示
例二: 超级玛丽
操作方向左上右下,计算机是0或1,所以需要对左上右下建立相应的模型。不能光计算,还要有模型,有了模型才能更好地去计算,去
解决现实世界的问题。
逻辑结构 >>数据对象中数据元素之间的相互关系
图形结构 树形结构 线性结构 集合结构

物理结构(存储结构)
1. 顺序存储结构(图书馆占一排9个座位) ArrayList源码分析
指的是用一段地址连续的存储单元依次存储线性表的数据元素

优点:
-
不用为表示节点间的逻辑关系而增加额外的存储开销。
-
具有按元素序号随机访问的特点。
缺点:
-
在做插入/删除操作时,平均每次移动表中的一半元素,因此表中数据量越大效率越低。
-
需要预先分配足够大的存储空间。过大可能会导致存储空间闲置,过小会造成溢出。
使用:
- 线性表的长度变化不大,且其主要操作是查找。
2. 链式存储结构(对不起,我是警察)
在计算机中用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的).
优点:
-
插入/删除方便(只需要修改指针)。
缺点:
-
要占用额外的存储空间存储元素之间的关系,存储密度低。
-
不是随机存储结构,不能随机存取元素,只能顺序存取。
使用:
- 线性表的长度变化较大,且其主要操作是插入/删除。
【数据结构】节点和结点,到底怎么区分?
要记住:一般算法中点的都是结点。我们在数据结构的图形表示中,对于数据集合中的每一个数据元素用中间标有元素值的方框表示,一般称它为数据结点,简称结点。
在链表数据结构中,链表中每一个元素称为“结点”,每个结点都应包括两个部分:一个是需要用的实际数据data;另一个就是存储下一个结点地址的指针,即数据域和指针域。
数据结构中的每一个数据结点对应于一个存储单元,这种储存单元称为储存结点,也可简称结点。
链表
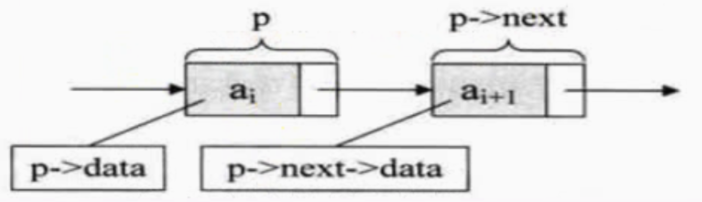
结点由存放元素的数据域和存放后继结点地址的指针域组成。
ai | ai+1 :结点/元素
p->next : 是一个指针(在java里就是引用),代表p的下一个结点
p->data | p->next->data : 结点的数据
前面的指针域存放的是后面结点的地址
在java里,p是对象,next是另一个对象。
public class P{
Object data;数据域,不关心是什么类型
//指针(java中是引用类型) c语言:指向下一个元素 java:引用下一个元素
P next;
}
P p1 = new P();
p1.data = "Danny";
P p2 = new P();
p1.next = p2;//表示p2是p1的next
单向链表
在链表结构中,每个结点仅本身需要存储的数据和下一个节点地址的这种链表结构,我们称为单链表结构,其示意图如下:

如图所示,在单链表中的每个节点中,除了数据区域外,还有一个区域存储了当前节点的下一节点的地址,我们把这个记录下个结点地址的指针或引用叫作后继指针或引用Next。
在我们的单链表结构中,有两个节点比较特殊,那就是第一个节点和最后一个节点。在链式存储结构中,我们将第一个节点称为头结点,将最后一个节点称为尾节点。
头节点记录链表的起始地址,有了这个地址,我们就可以遍历整个链表。尾节点的后继指针或者引用不是指向一个具体的节点,而是指向一个空地址NULL,从而表示该节点为链表的尾节点。
与数组一样,链表也支持数据的插入、查找、删除。
但是我们都知道,数组在进行数据的插入,删除操作时,为了保证内存数据的连续性,往往需要做大量的数据搬移工作,所以时间复杂度是O(n)。
而在链表中插入或删除数据时,因为链表结构中的节点并不需要连续的存储空间,所以在链表中进行数据的插入和删除时并不需要搬移节点。
对于链表的删除和插入操作,我们只需要调整相邻节点的后继指针即可,所以对应的时间复杂度是O(1)。
双向链表插入元素示例图
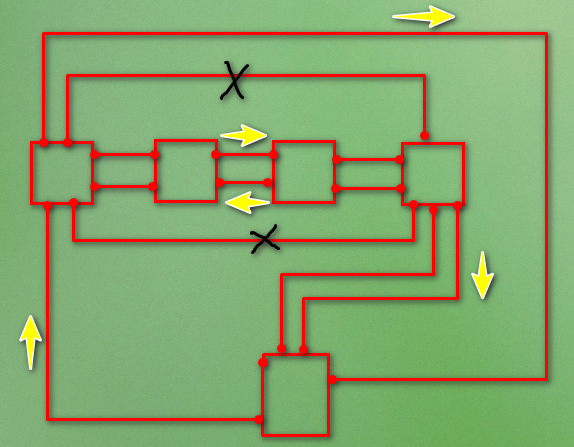

插入元素算法(重点)
Link:当前正在遍历的结点;lastLink:最后一个结点(全部遍历完才知道谁是最后结点)
Link<ET> link, lastLink;
public void add(ET object) {
if (expectedModCount == list.modCount) {
Link<ET> next = link.next; //现在link.next=a2; 所以next=a2
Link<ET> newlink = new Link<ET>(object, link, next);
lick.next = newlink; //a1指向新的结点
next.previous = newLink; //a2的前驱指向了newLink,也就是2那条线
link = newLink;当前结点变成了newLink
lastlink = null;
pos++;
expectedModCount++;
list.size++;
list.modCount++;
} else {
throw new ConcurrentModificationException();}
二分法查找
if(location<(size/2)){
for(int i = 0;i <= location;i++){
1ink = link. next;
} else{
for(int i = size;i > location;i--){
link = link. previous;
}
结点插入在前半段(从前往后):Next可以找到下一个结点 结点插入在后半段(从后往前):Previous可以找到前一个结点
remove
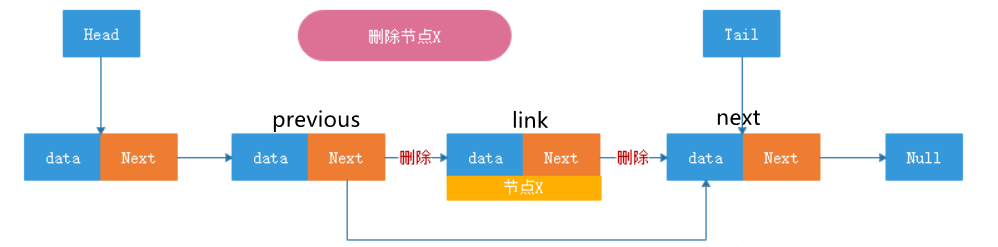
Link<E>previous=link.previous; 7
Link<E>next=link.next;
previous.next=next;
next.previous=previlus;
size--;
modCount++;
return link.data;


