函数式编程(一) 认识“编程范式”和“函数”
编程范式(Programming paradigm)
编程范式指我们在编写程序解决问题的思路和视角。它提供了同时也决定了程序员对程序运行的看法。计算机编程中存在许多编程范式,如命令式编程、声明式编程、面向对象编程以及结构化编程等等。其中面向对象编程范式认为程序是由一系列相互作用的对象组成,而结构化编程范式认为程序采用子程序、代码区块、for循环以及while循环等结构组成。下面主要说明本篇文章将要讲到的命令式编程范式和声明式编程范式。
1)命令式编程(Imperative):
强调程序代码模拟电脑运行过程,强调“先做什么”、“再做什么”。如果我们要计算“2*3+1”,我们编写代码时先计算2*3存入临时变量,再计算该临时变量与1的和。命令式编程是当前主流编程范式,我们编写的代码几乎都属于命令式编程范式。
2)声明式编程(Declarative):
强调程序代码模拟人脑计算过程,强调“最终要什么”,相比命令式编程范式来讲,它更看重结果而非过程。声明式编程范式更接近人类思想,它的思考层面要高于命令式编程。
下图显示了命令式编程范式与声明式编程范式的区别:
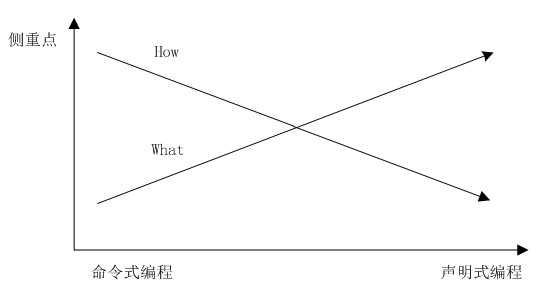
图1
注:各种编程范式之间并非都是对立的,很多范式是从不同角度来划分的。如面向对象编程范式同时也属于命令式编程范式。当然,本篇文章讲到的“命令式编程范式”和“声明式编程范式”两者是对立的。
声明式编程范式
声明式编程范式常见有以下两种(最常见):
1)领域特定语言(Domain Specific Language,DSL):
名字很陌生,但是我们却经常在用。如SQL、CSS以及正则表达式等等。这些语言只在特定领域起作用,并且使用这些语言时,我们大多数时候是在写“陈述、声明”的语句。如“select * from tb”,我们只关心我们要的结果,而不用去关系具体实现。
2)函数式编程(Functional Program,FP):
函数式编程是我们要讨论的重点。既然它属于声明式编程范式,那么它也应该强调结果(What)而非过程(How)。没错,函数式编程不同于常见的命令式编程,它不关心计算机具体的实现过程,而仅仅注重问题结果。
函数式编程(Functional Program):
网上关于“函数式编程”的解释有很多,但大多数都比较模糊抽象。维基百科上对函数式编程的解释是“In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data”,翻译成中文就是“函数式编程是一种编程范式,它将计算机运算看作是数学中函数的计算,并且避免了状态以及变量的概念”。这是个什么意思呢?很多文章分别从函数式编程的几个特点上做出了解释,比如“函数是第一公民”、“高阶函数(Higher Order Function)”、“无状态性(No State)”、“无副作用性(Side-Effect)”、“易于并行开发”以及“惰性求值”等等。但是我觉得这些都只是函数式编程的特点或者说是优点,并没有实质上解释出“函数式编程”与普通命令式编程的区别。我认为要搞清楚函数式编程,必须先认清“函数”的概念。没错,虽然我们自认为我们比较熟悉“函数”(或者叫“方法”,本文不区分这两者的区别),但是我们真的熟悉它们吗?
注:以后博客将依次介绍“函数式编程”以上几种特点。
编程函数和数学函数:
第一次了解“函数”的概念应该是我们读中学时,“y=x+1”在平面坐标系中是一条直线,到后来(不知道哪年级)学习了二次函数,“y=x^2+2*x+1”在平面坐标系中是一条抛物线。当时学习函数时知道以下知识点:
1)函数是一种映射,自变量经由一种映射关系变换后,得到因变量(函数值);
2)对于每个自变量,均能、有且仅有一个因变量与之对应,这是函数的确定性。也就是说,给定一个自变量,任何时候函数值都唯一;
那么,到大学学习编程后(本人读大学才开始学习编程),我们在程序中又遇见了“函数”,很熟悉的感觉。但是它和数学中的函数有什么关联呢?也就是说,数学思想与我们编程思想是否有关联?如果以我们目前写C#、Java、C++等代码来看,它们几乎没有关系,因为我们程序中的函数可以没有参数(数学函数中的“自变量”),也可以没有返回值(数学函数中的因变量),就算一个函数有返回值,那么给定参数,调用函数后每次运行结果也可能不一样。以上这些均不能满足数学函数的概念。其实出现“两种函数几乎无关系”的现象很容易理解,数学描述的是人类思维过程,而我们(目前大部分人)编写的程序代码描述的是计算机运行过程。在数学家与程序员之间早已产生了沟通障碍,比如下图:
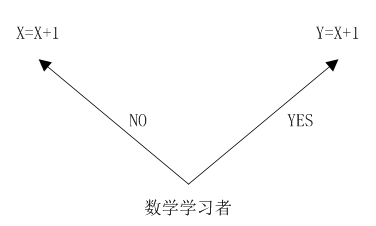
图2
如上图所示,“X=X+1”这种表达式如果从数学角度来看,几乎是不可成立的,让任何一个没有学过编程的人去看这个表达式,TA都会以为你写的是错的,他们只认“Y=X+1”。原因很简单,在程序中,符号可以代表变量,而变量表示一个内存单元,该内存处的值可以被重写(赋值);而在数学中,符号永远只是符号,等号“=”两边表示等价关系,“Y=X+1”表示Y与X+1是等价的,Y仅仅是X+1的一个代替符号。
同理,函数也一样。数学中的函数仅仅描述一种“映射关系”,给定一个自变量,我们可以得到一个因变量,仅此而已。而程序中的函数更多的时候扮演的是一种“功能”角色,它能够完成指定任务。当然,如果程序中一个函数包含参数,并且能够返回值,那么它完全可以模拟数学函数。下面使用C#编写一个委托,它代表数学中的一个一元函数:
1 public delegate double Function1X(double x);
如上代码所示,委托签名中包含一个double类型参数,并且返回一个double类型返回值。数学中的“f(x)=x^2+2*x+1”可以使用C#编写以下函数:
1 public double f(double x) 2 { 3 return Math.Pow(x,2) + 2*x + 1; 4 }
函数f(x)在x=2处的值调用代码:f(2);。或者使用Lambda表达式:
x => Math.Pow(x,2) + 2*x + 1;
程序中的函数接收一个double类型参数,经过映射关系,返回一个double类型的返回值,它与“f(x)=x^2 + 2*x +1”对应。那么数学函数中的二元函数在程序中怎样表示呢?很简单,二元函数包含两个自变量,我们只需要为程序中函数定义两个参数即可:
1 public delegate double Function2XY(double x,double y);
如上代码所示,委托签名中包含两个double类型参数,并且返回一个double类型返回值。
从上面的介绍可以看出,如果将程序中函数做一些限制,那么它就可以模拟数学中的函数了:
1)每个函数必须包含输入参数(作为自变量);
2)每个函数必须有返回值(作为因变量);
3)无论何时,给定参数调用函数时,返回值必须一致。
上面第三条限制是为了满足函数的“确定性”,该条限制要求程序中的函数执行期间不能依赖于外界因素,也不要影响外部环境。换句话说,它在执行期间与外界是隔绝的。我们将满足以上条件的函数称为“纯函数(Pure Function)”。纯函数与外界交互只有一条渠道——传入参数与返回值。纯函数也不读取/改变全局变量、无IO操作等。

图3
纯函数是程序代码模拟数学函数的基础。理论上讲,函数式编程中,函数是第一公民的同时,所有函数也都应该属于“纯函数”。到此,我们再回过头看一下维基百科上对“函数式编程”的解释:函数式编程是一种编程范式,它将计算机运算看作是数学中函数的计算,并且避免了状态以及变量的概念。很显然,函数式编程向数学验算靠拢,使用一种平时正常的数学思维去解决问题。
注:函数式编程是基于“lambda验算(Lambda Calculus)”的,它并不属于“图灵机”理论范畴。我没搞清楚lambda验算,所以本文并没详细提到。看到Lambda很容易让我们想到C#3.0中引入的Lambda表达式,这不是偶然。C# 3.0之后开始支持“函数式编程”,后面文章将会讲到。
(未完待续)




