ImageSharp源码详解之JPEG压缩原理（4）熵编码

熵编码这一过程可以算是JPEG过程中最为复杂一部分，本身的数学难度并不大，但是概念太多很容易搞混。比如很多博客直接将这部分省略成霍夫曼编码，我认为这种说法很不准确，因为这里的熵编码是多种编码技术综合运用的。

1.编码过程

上一章，我们将原始图像数据进行量化，得到一个8*8的数据块，这个数据块还要经历下面这些步骤才最终转换为JPEG格式数据：

(1)将8*8的数据块分成两个分量直流系数(DC)和交流系数进(AC)

(2)对AC分量进行之字排列，然后使用行程长度编码(RLE)进行编码，然后查询两张表（标准分类表和霍夫曼标准表）将数据编码写入数据流。

(3)使用差分编码(DPCM)对DC进行编码，然后查询两张表（标准分类表和霍夫曼标准表）将数据编码写入数据流。

注意：不同的代码会有不同的实现，ImageSharp编码使用标准霍夫曼表，我看了一眼谷歌的guetzli，里面就有构建霍夫曼树的过程。

下面结合上文的例子，详细介绍这3个过程。

1.1 DC和AC分量解释

我们在经过DCT变换的时候说过一句，就是DCT变化使得主要的能量都集中在左上角，所以我们可以做个试验，就只保留左上角的几个数据，其余全部设为0，可以看到生成JPEG的图像清晰度如下：

　　　　原图(173k) 　　　保留AC分量3个数据(100k)

　　保留AC分量2个数据(92.3k)　　　　　　　　不保留AC分量(70.1k)

可以看到保留的数据越多，图像就越清晰，但是数据量也越大，所谓DC分量可以看做这个8*8数据块的平均值倍数，而AC分量就是这个8*8数据中的差异值了。

1.2 AC分量“之”字扫描(Zig-Zag)及行程编码

好了，终于到这一步了，一般资料都是先描述DC分量如何编码，然后是AC分量，但是我先写AC分量的行程编码是因为这一步是整个JPEG编码过程中真正实现压缩的一个步骤，前面的数据进过DCT、量化后原始数据只是“有损”、并没有“压缩”，比如有一个数据块内容如下：

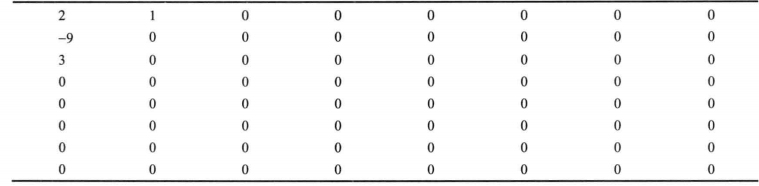
量化后的8*8数据块

我们把这个数据块写入数据流中，还是一样的占用8*8*8bit（忽略负号）并没有因为量化而减少需要存储的字节，但是大家看到右下角有这么多重复的0，肯定很容易就想可以使用一些方法将多余的0给省略掉，JPEG使用的是行程编码的方法，为了保证低频分量先出现，高频分量后出现，这里就使用“之”字型(Zig-Zag)的排列方法，如下图所示。

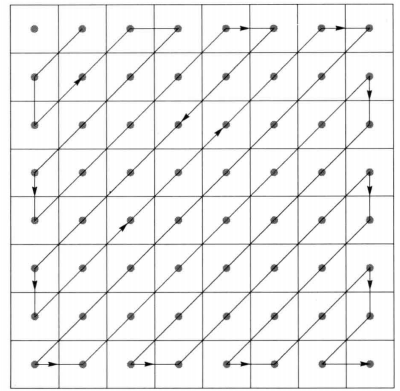
8*8变换“之”字扫描

在进过zig变换后，上面数据块中AC分量变成以下序列：

1 -9 3 0 0 0 ....0 bit数=63*8bit(请暂时忽略-9的负号吧)

然后进行行程编码(RLE)，行程编码原理非常简单，我们使用字符串举例，如果待压缩串为"AAABBBBCBB"，则压缩的结果是(A,3)(B,4)(C,1)(B,2)，可以看出，如果相邻字符重复情况越高，则压缩效率就较高。经过行程编码，JPEG图像被大幅度的压缩了，如上面序列变成下面序列：

(1,1) (-9,1) (3,1) (0,60) bit数≈8*8bit

看到没有数据压缩了将近8倍。如果到这里就结束，JPEG的压缩率已经很高了，但其实并没完，真正的AC分量在这里的是行程编码，查询分类列表和霍夫曼编码的综合运用，在这一块各种概念错综复杂，看的我很头疼，对于如何将AC分量的编码写入数据流中，这里先按下不表，正所谓花开两朵各表一枝，我们再说DC分量的情况。

1.3 DC分量的差分编码及霍夫曼编码

我之前在网上搜关于差分编码DPCM的相关信息，坦白说完全看不懂，但是在JPEG这里的实现非常简单，无非就是记录两个DC分量的差值，所以略过DPCM的复杂背景，我们直接看DC分量如何编码的就行：

首先我们要知道，将比如-6这个数值写入数据流中，需要两次编码，第一次先查询一个标准分类表，该表在AC分量中也会使用，该表如下：

实际数值	类别	编码
0	0	-
-1,1	1	0,1
-3,-2,2,3	2	00,01,10,11
-7,-6,-5,-4,4,5,6,7	3	000,001,010,011,100,101,110,111
-15,……,-8,8,……,15	4	0000,……,0111,1000,……,1111
-31,……,-16,16,……,31	5	00000,……,01111,10000,……,11111
-63,……,-32,32,……,63	6	……
-127,……,-64,64,……,127	7	……
-255,……,-128,128,……,255	8	……
-511,……,-256,256,……,511	9	……
-1023,……,-512,512,……,1023	10	……
-2047,……,-1024,1024,……,2047	11	……
-4095,……,-2048,2048,……,4095	12	……
-8191,……,-4096,4096,……,8191	13	……
-16383,……,-8192,8192,……,16383	14	……
-32767,……,-16384,16384,……,32767	15	……

标准分类表

注意这种表的输入和输出，输入是实际的数值比如-5、23等，输出是这个数值的类别和它在类别中的编码，比如输入-5，输出就是(3,010)，你也可以这么理解这张表，就是一个数值如果是正数，直接转换成二进制就是它的编码，类别就是二进制编码的长度；如果是负数，取反码，类别同样是反码的长度，在程序中就是这么求出标准分类表的。

回到编码上来，我们先将数据块中的DC分量与上一个数据块中的DC分量做差，比如得出一个值为-6，然后我们查询标准该表，在类别为3的数据中用“001”表示，于是我们往数据流中写入“huftab(3),001”。huftab(3)表示类别为3的霍夫曼编码，001就是表中的编码。问题来了，3的霍夫曼编码是多少呢？这就看不同的代码实现了，如果我们使用标准的霍夫曼DC编码表，参考JPEG国际标准可以看到光亮度DC差值霍夫曼表如下(色度表略过)：

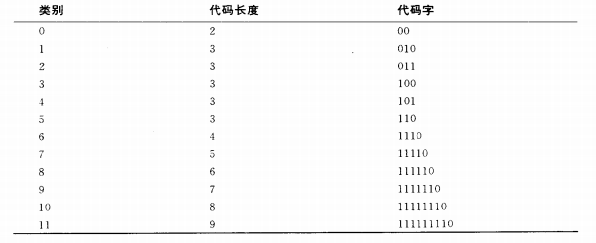
光亮度DC差值霍夫曼表

然后我们就知道类别3的代码字为“100”，所以-6这个字我们会写成“100001”，现在编码成了6bit，所以这个步骤中也有压缩，但是如果数字过大比方说32767 ，那么不仅不会减小比特数，还会比原来更大，但是根据统计，一般不会出现超过长度为10的情况。

另外有一个问题就是我们使用的是标准霍夫曼编码表，它是根据统计制作的，从解码的角度考虑，存储的时候哈夫曼编码条目不一定能够还原回去，所以有的编码器使用标准霍夫曼表编码，而有的编码器则要生成自己的霍夫曼编码表。

1.4 AC分量的霍夫曼编码

我们单独再举个例子来解释，有一个zig变换后的序列：

1 -9 3 0 0 0 5 5....0

我们通过查询分类表和行程编码可以编码如下(注意这里的行程编码是记录前面有多少位0值)：

(huftab(0/1),1) (huftab(0/4),0110) (hufftab(0/2),11) (hufftab(3/3),101) (hufftab(0/3),101) (huf(EOB))

我们先从第一个值1开始说明，1在分类表中表里面属于类别1，编码1，前面有0个零值所以编码是huftab(0/1),1 。huftab(0/1)代表的是0/1在霍夫曼表中的编码。

第二个值是-9在分类表中属于类别4，编码0110，前面有0个零值所以编码为 huftab(0/4),0110

同理3在分类表中属于类别2，编码11，前面有0个零值所以编码为 hufftab(0/2),11

然后我们看下一个值是5，类别3，编码101，前面有3个零值，所以编码为hufftab(3/3),101

下一个5的类别3，编码101，前面0个零值，所以编码为hufftab(0/3),101

在此之后标记都为0，就发生EOB的霍夫曼编码。

这里还有个问题，huftab(0/1)，huftab(0/4)，huf(EOB)等等这些编码到底是什么，这里依然看各自代码实现，大部分选中的是查询标准霍夫曼AC编码表，

我这里是部分光亮度AC系数的霍夫曼表，全部的表很长，这里只是一部分：

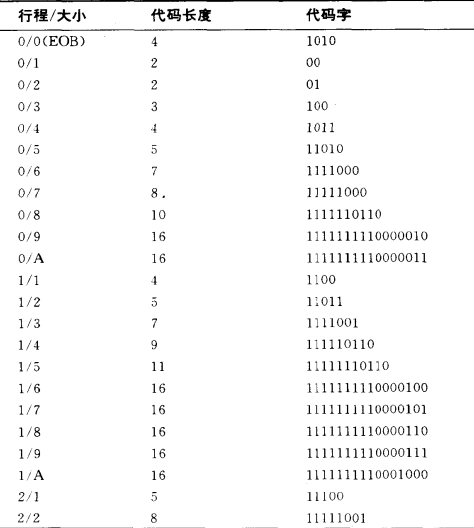
光亮度AC系数霍夫曼表

所以上面序列可以完全编码为：001 10110110 0111 111111110101101 100101 1010 （空格是我自己添加的，方便阅读，实际没有），大家可以数一下不到30个bit，比起63*8bit少了太多了。

2.代码实现

这里的代码写的非常简单了，先创建了一个标准分类表：

　　　　　/// <summary>
        /// Gets the counts the number of bits needed to hold an integer.
        /// </summary>
        // The C# compiler emits this as a compile-time constant embedded in the PE file.
        // This is effectively compiled down to: return new ReadOnlySpan<byte>(&data, length)
        // More details can be found: https://github.com/dotnet/roslyn/pull/24621
        private static ReadOnlySpan<byte> BitCountLut => new byte[]
            {
                0, 1, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5,
                5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6,
                6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6,
                7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7,
                7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7,
                7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7,
                7, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,
                8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,
                8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,
                8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,
                8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,
                8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,
                8, 8, 8,
            };

这个数组大家仔细看是不是和我们上面的标准分类的排列非常类似，程序使用查表的方法，将输入的数字转换为类别，然后再根据不同的霍夫曼表类型，查询不同的霍夫曼表，霍夫曼标准表定义在HuffmanSpec这个结构体重，最后写入outputStream中。

 1         /// <summary>
 2         /// Emits a run of runLength copies of value encoded with the given Huffman encoder.
 3 　　　　 /// 将值写入霍夫曼行程编码中，这里将DC的也强行写到这个方法里面来有点不妥吧，然后用HuffIndex来区分是哪种表
 4 　　　　 /// </summary>
 5         /// <param name="index">The index of the Huffman encoder(枚举类型：DC亮度，AC亮度，DC色度，AC色度)</param>
 6         /// <param name="runLength">The number of copies to encode（前面有多少个零值）</param>
 7         /// <param name="value">The value to encode（这个系数实际值）</param>
 8         [MethodImpl(MethodImplOptions.AggressiveInlining)]
 9         private void EmitHuffRLE(HuffIndex index, int runLength, int value)
10         {
11             int a = value;
12             int b = value;
13             if (a < 0)
14             {
15                 a = -value;
16                 b = value - 1;
17             }
18 　　　　　　　//value输入的值，bt输出类别
19             uint bt;
20             if (a < 0x100)
21             {
22                 bt = BitCountLut[a];
23             }
24             else
25             {
26                 bt = 8 + (uint)BitCountLut[a >> 8];
27             }
28 　　　　　　　//如果是AC，将行程长度与类别合成霍夫曼编码，写入数据流
29 　　　　　　　//如果是DC，行程长度为0，与类别合成霍夫曼编码，写入数据流
30             this.EmitHuff(index, (int)((uint)(runLength << 4) | bt));
31             if (bt > 0)
32             {
33 　　　　　　　　　　//如果类别不是0，那么将这个标准分类code写入数据流
34                 this.Emit((uint)b & (uint)((1 << ((int)bt)) - 1), bt);
35             }
36         }

View Code

在看一下EmitHuff这个方法，这个方法就是根据DC亮度、AC亮度、DC色度、AC色度等查询不同的霍夫曼表，最后写入数据流：

 1  /// <summary>
 2         /// Emits the given value with the given Huffman encoder.
 3         /// </summary>
 4         /// <param name="index">The index of the Huffman encoder</param>
 5         /// <param name="value">The value to encode.</param>
 6         [MethodImpl(MethodImplOptions.AggressiveInlining)]
 7         private void EmitHuff(HuffIndex index, int value)
 8         {
 9             uint x = HuffmanLut.TheHuffmanLut[(int)index].Values[value];
10             this.Emit(x & ((1 << 24) - 1), x >> 24);
11         }

View Code

最后解释一下Emit这个方法，我们都知道JPEG格式是按照二进制来存储数据的，但我们都知道，向数据流中写入最小单位必须是byte也就是8个bit，所以Emit这个方法最主要作用就是读取当前要存数据的长度，如果不足8bit，就将剩余数据放进accumulatedBits字段中，等待下次执行Emit方法时，拼凑成8bit再写入。

 1  　　/// <summary>
 2         /// Emits the least significant count of bits of bits to the bit-stream.
 3         /// The precondition is bits
 4         /// <example>
 5         /// &lt; 1&lt;&lt;nBits &amp;&amp; nBits &lt;= 16
 6         /// </example>
 7         /// .
 8         /// </summary>
 9         /// <param name="bits">The packed bits.</param>
10         /// <param name="count">The number of bits</param>
11         private void Emit(uint bits, uint count)
12         {
13             count += this.bitCount;
14             bits <<= (int)(32 - count);
15             bits |= this.accumulatedBits;
16 
17             // Only write if more than 8 bits.
18             if (count >= 8)
19             {
20                 // Track length
21                 int len = 0;
22                 while (count >= 8)
23                 {
24                     byte b = (byte)(bits >> 24);
25                     this.emitBuffer[len++] = b;
26                     if (b == 0xff)
27                     {
28                         this.emitBuffer[len++] = 0x00;
29                     }
30 
31                     bits <<= 8;
32                     count -= 8;
33                 }
34 
35                 if (len > 0)
36                 {
37                     this.outputStream.Write(this.emitBuffer, 0, len);
38                 }
39             }
40 
41             this.accumulatedBits = bits;
42             this.bitCount = count;
43         }