2024 Datawhale X 李宏毅苹果书 AI 夏令营第5期——跟李宏毅学深度学习(入门)
《深度学习详解》主要内容源于《机器学习》（2021年春），选取了《机器学习》（2017年春） 的部分内容，在这些基础上进行了一定的原创，补充了不少除这门公开课之外的深度学习相关知识。为了尽可能地降低阅读门槛，笔者对这门公开课的精华内容进行选取并优化，对所涉及的公式都给出详细的推导过程，对较难理解的知识点进行了重点讲解和强化，以方便读者较为轻松地入门。
本方向学习目标
本方向的核心学习目标是——通过《深度学习详解》和 李宏毅老师 21年的机器学习课程视频，入门机器学习，并尝试学习深度学习，展开代码实践（选修）。
相关学习链接👇
Task1——$\S$1.1 通过案例了解机器学习(2024/8/24-27)
机器学习分类
机器学习就是让机器具备找一个函数的能力。
机器学习分类（根据要找的函数不同）：
- 回归(regression)：假设要找的函数的输出是一个数值，一个标量(scalar)，这种机器学习的任务称为回归。例如：预测未来某一个时间的 PM2.5的数值。
- 分类(classification)：分类任务要让机器做选择题。人类先准备好一些选项，这些选项称为类别(class)，现在要找的函数的输出就是从设定好的选项里面选择一个当作输出，该任务称为分类。分类不一定只有两个选项，也可以有多个选项。例如：检测垃圾邮件。
- 结构化学习(structured learning)：机器不只是要做选择题或输出一个数字，而是产生一个有结构的物体。例如：让机器画一张图，写一篇文章。这种叫机器产生有结构的东西的问题称为结构化学习。
机器学习流程
Step1：写出含有未知数的函数(即模型) \({y=b+w*x_1}\) 。其中 \(w\) 为权重(weight)，\(b\) 为偏置(bias)。
Step2：定义损失函数 \(L(b,w)\)。其输入为模型参数 \(w\) 和 \(b\)，损失函数衡量预测值与真实值之间的差距，计算方法有
- 平均绝对误差 MAE：\(e=|\hat {y}-y|\)
- 均方误差 MSE：\(e=(\hat {y}-y)^2\)
- 交叉熵：预测值和真实值为概率分布
Step3：解最优化问题，找到使损失函数值最小的参数 \(w^*\) 和 \(b^*\) 。常用的优化方法有 梯度下降法。
Task2——$\S$1.2 了解线性模型(2024/8/28-31)
由于初始预测模型 \(y=b+w*x_1\) 表现不理想，通过领域知识(包括观察数据等)，需要对初始模型进行修改。观察到真实数据呈周期变化，重构初始模型，得到：
线性模型：$$y=b+{\sum_{j=1}^{N} {w_j x_j}}$$
但是，当输入特征 \(x_1\) 与预测结果 \(y\) 之间的关系不是一条直线，此时线性模型无法模拟真实复杂的关系。
由于线性模型的限制(模型的偏差)，因此还需对线性模型进行进一步优化，其中优化模型有：
分段线性曲线：
分段线性曲线可以逼近任何曲线，其可以看作常数与一系列 Hard Sigmoid 函数的组合。即：
- Hard Sigmoid 函数与 Sigmoid 函数
由于 Hard Sigmoid 函数的表达式不易直接写出，进一步可以用较为容易表示的 Sigmoid 函数来逼近 Hard Sigmoid 函数。Sigmoid 函数的表达式为：
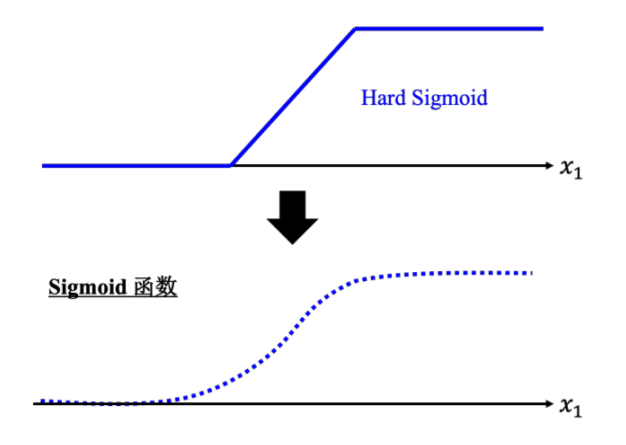
因此，任意曲线都可以由一系列 Sigmoid 函数和常数的组合表示。
- Hard Sigmoid 函数与 ReLU 函数
Hard Sigmoid 函数可看作两个修正线性单元(Rectified Linear Unit, ReLU)的加总。ReLU 的公式为：
激活函数：
在机器学习里，常见的激活函数有 Sigmoid 函数或 ReLU 函数等。
Task3——$\S$2 机器学习框架&实践攻略(2024/9/1-3)
影响模型训练的一些因素
-
模型偏差
选择的机器学习模型过于简单，不足以表示输入和输出之间复杂的函数关系。
解决方法：重新构建模型，增加模型灵活性。 -
优化问题
一般采用梯度下降进行优化，存在陷入局部最小值的情况。
解决方法：通过比较不同模型来判断模型现在够不够大。 -
过拟合
训练集上的结果好，但是测试集上的损失很大的情况。
解决方法：增加训练集，做数据增强；或者给模型限制，降低莫模型灵活性。 -
交叉验证
k折交叉验证，解决随机划分验证集造成结果差的问题。 -
不匹配
训练集和测试集的分布不同的情况。
选修——尝试进行代码实践(2024/9/3)
posted on 2024-08-26 11:02 xiaoyufuture 阅读(43) 评论(0) 编辑 收藏 举报
