2 模型【训练模型】
训练模型和测试模型
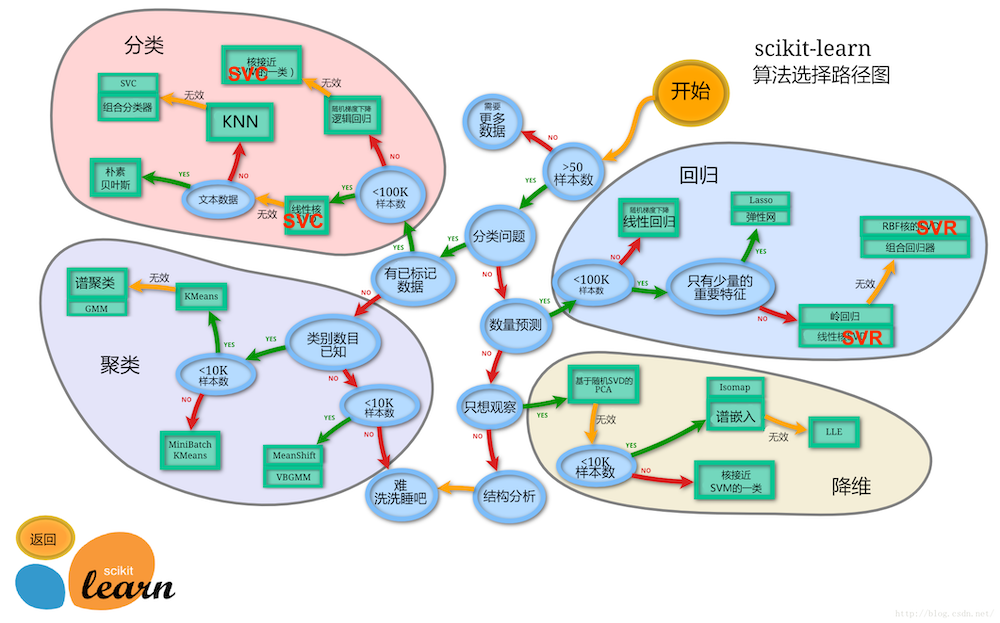
由图中,可以看到库的算法主要有四类:分类,回归,聚类,降维。其中:
- 常用的回归:线性、决策树、SVM、KNN ;
- 集成回归:随机森林、Adaboost、GradientBoosting、Bagging、ExtraTrees
- 常用的分类:线性、决策树、SVM、KNN,朴素贝叶斯;
- 集成分类:随机森林、Adaboost、GradientBoosting、Bagging、ExtraTrees
- 常用聚类:k均值(K-means)、层次聚类(Hierarchical clustering)、DBSCAN
- 常用降维:LinearDiscriminantAnalysis、PCA
这个流程图代表:蓝色圆圈是判断条件,绿色方框是可以选择的算法,我们可以根据自己的数据特征和任务目标去找一条自己的操作路线。
鸢尾花识别是一个经典的机器学习分类问题,它的数据样本中包括了4个特征变量,1个类别变量,样本总数为150。
它的目标是为了根据花萼长度(sepal length)、花萼宽度(sepal width)、花瓣长度(petal length)、花瓣宽度(petal width)这四个特征来识别出鸢尾花属于山鸢尾(iris-setosa)、变色鸢尾(iris-versicolor)和维吉尼亚鸢尾(iris-virginica)中的哪一种。
1、训练模型
我们想要利用这些数据构建一个机器学习模型,用于预测新测量的鸢尾花的品种。但在将 模型应用于新的测量数据之前,我们需要知道模型是否有效,也就是说,我们是否应该相 信它的预测结果。 不幸的是,我们不能将用于构建模型的数据用于评估模型。因为我们的模型会一直记住整 个训练集,所以对于训练集中的任何数据点总会预测正确的标签。这种“记忆”无法告诉 我们模型的泛化(generalize)能力如何(换句话说,在新数据上能否正确预测)。 我们要用新数据来评估模型的性能。新数据是指模型之前没有见过的数据,而我们有这些新数据的标签。通常的做法是将收集好的带标签数据(此例中是 150 朵花的测量数据) 分成两部分。一部分数据用于构建机器学习模型,叫作训练数据(training data)或训练 集(training set)。其余的数据用来评估模型性能,叫作测试数据(test data)、测试集(test set)或留出集(hold-out set)。
1、确定训练集以及测试集
- 莺尾花样本数量150个
- 属于一个分类问题
- 有已标记的数据
- 样本小于100K
- 线性核
from sklearn.model_selection import train_test_split
""" train_test_split 函数利用伪随机数生成器将数据集打乱 """
X_train, X_test, y_train, y_test = train_test_split(iris['data'], iris['target'], test_size=0.3, random_state=0)
""" X_train 包含 75% 的行数据,X_test 包含剩下的 25% """
print(X_train)
print(X_test)
print(y_test)
print(y_train)
2、训练模型
选择对应的方法,开始训练我们的模型。
from sklearn.svm import SVC
# from sklearn.svm import LinearSVC
""" 当probability=True时,才能打印分类概率 """
clf = SVC(kernel='linear', probability=True)
# clf = LinearSVC()
""" 训练模型 """
clf.fit(X_train, y_train)
""" 预测数据分类结果 """
y_prd = clf.predict(X_test)
y_prd
3、用测试集简单测试一下我们的模型
y_prd-y_test

4、测试概率
用我们的测试集来演示预测测试集中的每个花跟上面三种花的相似程度。
# 打印预测概率
clf.predict_proba(X_test)[:5, :]
5、查看模型得分
评估我们的模型可用程度
clf.score(X_test, y_test)
2、测试模型
当我们训练出我们的数据之后,我们需要知道我们训练出来的模型是否准确,以及模型的性能等等方面。本小节来讲解一下怎样通过sklearn.metircs来度量模型的性能以及使用sklearn.model_selection下的模块来评估模型的泛化能力。
# 使用metrics 测试模型打印精确度/召回率/F1值()
from sklearn.metrics import classification_report
print(classification_report(y_test, clf.predict(X_test), target_names=iris.target_names))
得到的结果是:
precision recall f1-score support
精确度 召回率 F1值
setosa 1.00 1.00 1.00 16
versicolor 1.00 0.94 0.97 18
virginica 0.92 1.00 0.96 11
accuracy 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
算法逻辑
对于数据测试结果有下面4种情况:
TP: 预测为正, 实现为正
FP: 预测为正, 实现为负
FN: 预测为负,实现为正
TN: 预测为负, 实现为负
准确率: TP/ (TP + FP)
召回率: TP/(TP + FN)
F1-score: 2TP/(2TP + FP + FN)
交叉验证
一般会把数据按照某种比例分为训练集、测试集。训练集用来训练模型,把测试集当做未来新样本的样本集用来评估模型。然后交叉验证可以认为就是不断地重复训练模型、测试模型。如果数据量较大的话,会把训练集按照某种比例分成训练集、验证集、测试集,使用训练集训练参数;使用验证集训练超参数;使用测试集测试模型性能。
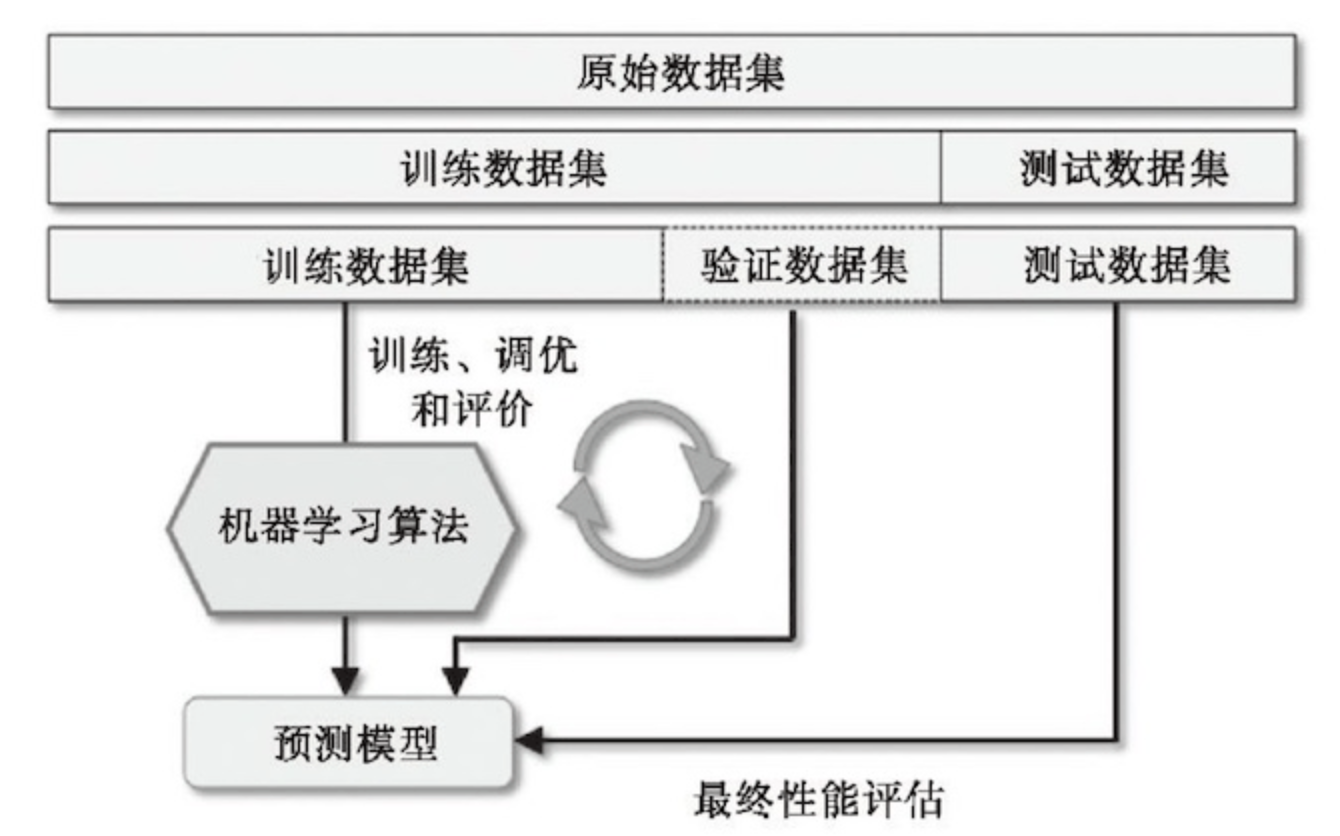
-
简单交叉验证
把数据集按照某种比例,将数据集中的数据随机的分为训练集和测试集。然后不断的改变模型参数训练出一组模型,每训练完一个模型就用测试集测试,最后得到性能最好的模型。
# 简单交叉验证 from sklearn.model_selection import train_test_split # 导入鸢尾花数据 X = iris.data[:, [0, 1]] y = iris.target # random_state=1可以确保结果不随机,stratify=y可以确保每个分类的结果都有相同的比例 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y) print('不同类别所有样本数量:{}'.format(np.bincount(y))) print('不同类别训练数据数量:{}'.format(np.bincount(y_train))) print('不同类别测试数据数量:{}'.format(np.bincount(y_test)))不同类别所有样本数量:[50 50 50] 不同类别训练数据数量:[35 35 35] 不同类别测试数据数量:[15 15 15]将模型分为10个,获取各个模型的得分
from sklearn.model_selection import cross_val_score score = cross_val_score(clf, X_test, y_test, cv=10) score
打印模型的平均得分和置信区间
print('准确率:{:.4f}(±{:.4f})'.format(score.mean(), score.std()*2))
-
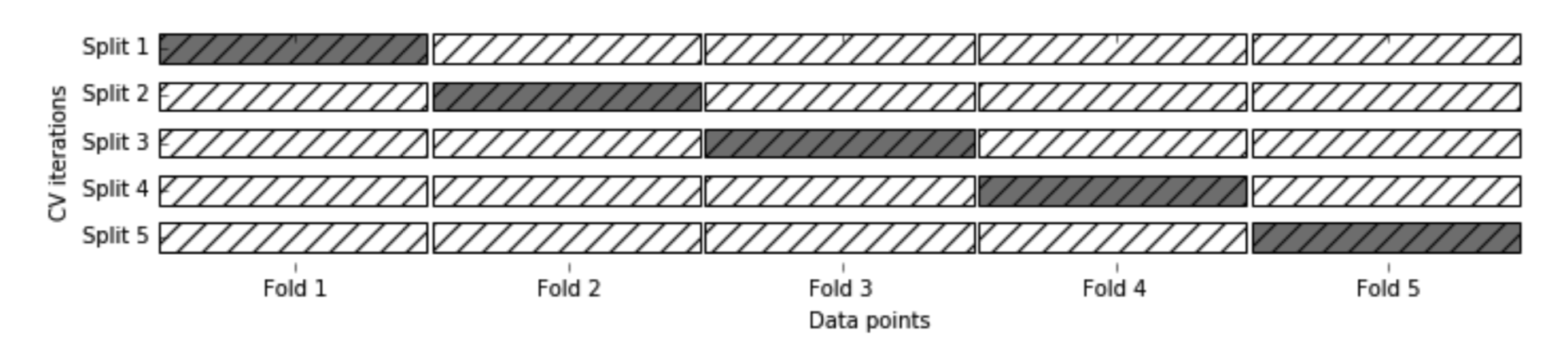
分层K折交叉验证
将数据随机的分为(k)个子集((k)的取值范围一般在([1-20])之间),然后取出(k-1)个子集进行训练,另一个子集用作测试模型,重复(k)次这个过程,得到最优模型。
# k折交叉验证 # StratifiedKFold会按照原有标签的分布情况对数据分层 from sklearn.model_selection import StratifiedKFold # 导入鸢尾花数据 X = iris.data[:, [0, 1]] y = iris.target # n_splits=10相当于k=10 kfold = StratifiedKFold(n_splits=3, random_state=1) kfold = kfold.split(X, y) for k, (train_data, test_data) in enumerate(kfold): print(train_data,test_data) print('迭代次数:{}'.format(k), '训练数据长度:{}'.format( len(train_data)), '测试数据长度:{}'.format(len(test_data)))结果:
[ 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149] [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116] 迭代次数:0 训练数据长度:99 测试数据长度:51 [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149] [ 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133] 迭代次数:1 训练数据长度:99 测试数据长度:51 [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133] [ 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149] 迭代次数:2 训练数据长度:102 测试数据长度:48

