概率论-熵和信息增益

熵和信息增益

熵（Entropy）

  熵表示随机变量不确定性的度量。假设离散随机变量\(X\)可以取到\(n\)个值，其概率分布为

\[P(X=x_i)=p_i, \quad i = 1,2,\ldots,n \]

则\(X\)的熵定义为

\[H(X) = -\sum_{i=1}^n p_i log{p_i} \]

由于熵只依赖\(X\)的分布，与\(X\)本身的值没有关系，所以熵也可以定义为

\[H(p) = -\sum_{i=1}^n p_i log{p_i} \]

  熵越大，则随机变量的不确定性越大，并且\(0\geq{H(p)}\leq\log{n}\)。

  当随机变量只取两个值\(0\)和\(1\)的时候，\(X\)的分布为

\[P(X=1)=p, \quad P(x=0)=1-p, \quad 0\geq{p}\leq{1} \]

熵则是

\[H(p) = -p\log_2 p-(1-p) \log_2(1-p) \]

此时随机变量为伯努利分布，熵随概率变化的曲线如下图所示

import numpy as np
from math import log
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

p = np.arange(0.01, 1, 0.01)
entro = -p*np.log2(p) - (1-p)*np.log2(1-p)

plt.plot(p, entro)
plt.title('伯努利分布时熵和概率的关系', fontproperties=font)
plt.xlabel('p')
plt.ylabel('H(p)')
plt.show()

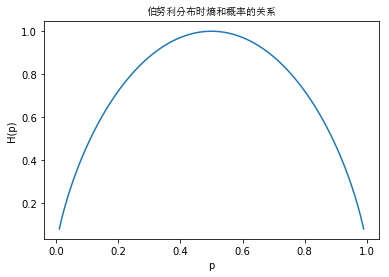
  当\(p=0\)和\(p=1\)时熵值为\(0\)，此时随机变量完全没有不确定性；当\(p=0.5\)时的熵值最大，随机变量的不确定性最大。

条件熵（Conditional Entropy）

  假设有随机变量\((X,Y)\)，其联合概率为

\[p(X=x_i,Y=y_i), \quad i=1,2,\ldots,n; \quad j=1,2,\ldots,m \]

  条件熵\(H(Y|X)\)表示在已知随机变量\(X\)的条件下随机变量\(Y\)的不确定性，定义为

\[H(Y|X) = \sum_{i=1}^n P(X=x_i) H(Y|X=x_i) \]

通过公式可以把条件熵理解为在得知某一确定信息的基础上获取另外一个信息时所获得的信息量。

  当熵和条件熵中的概率由数据估计获得时，所对应的熵与条件熵分别称为经验熵（empirical entropy）和经验条件熵（empirical conditional entropy）。

联合熵（Joint Entropy）

  假设有随机变量\((X,Y)\)，其联合概率为

\[p(X=x_i,Y=y_i)=p_{ij}, \quad i=1,2,\ldots,n; \quad j=1,2,\ldots,m \]

  联合熵度量的是一个联合分布的随机系统的不确定性，它的定义为

\[H(X,Y) = -\sum_{i=1}^n \sum_{j=1}^m p(X=x_i,Y=y_j) \log{p(X=x_i,Y=y_j)} \]

由此可以对联合熵进行简单的化简

\[\begin{align} H(X,Y) & = -\sum_{i=1}^n \sum_{j=1}^m p(X=x_i,Y=y_j) \log{p(X=x_i,Y=y_j)} \\ & = -\sum_{i=1}^n \sum_{j=1}^m p(X=x_i,Y=y_j) \log{p(X=x_i)\log{p(Y=y_i|X=x_i)}} \\ & = -\sum_{i=1}^n \sum_{j=1}^m p(X=x_i,Y=y_j) \log{p(X=x_i)} -\sum_{i=1}^n \sum_{j=1}^m p(X=x_i,Y=y_j) \log{p(Y=y_i|X=x_i)}\\ & = -\sum_{i=1}^n p(X=x_i) \log{p(X=x_i)} -\sum_{i=1}^n \sum_{j=1}^m p(X=x_i,Y=y_j) \log{p(Y=y_i|X=x_i)} \\ & = H(X) + H(Y|X) \end{align} \]

同理可证\(H(X,Y)=H(Y)+H(X|Y)\)，即联合熵表示对一个两个随机变量的随机系统，可以先观察一个随机变量获取信息，在这之后可以在拥有这个信息量的基础上观察第二个随机变量的信息量，并且无论先观察哪一个随机变量对信息量的获取都是没有任何影响的。

  同理可得一个含有\(n\)个独立的随机变量的随机系统\((X_1,X_2,\ldots,X_n)\)的联合熵为

\[H(X_1,X_2,\ldots,X_n) = \sum_{i=1}^n H(X_i) \]

可以发现即使是含有\(n\)个随机变量的随机系统无论先观察哪一个随机变量对信息量的获取也是没有任何影响的。

相对熵（Relative Entropy）

  相对熵有时候也称为KL散度 (Kullback–Leibler divergence)。

  设\(p(x)\)、\(q(x)\)是离散随机变量\(X\)中取值的两个概率分布，则\(p\)对\(q\)的相对熵是：

\[\begin{align} DKL(p||q) & = \sum_{i=1}^n p(X=x_i)\log{\frac{p(X=x_i)}{q(X=x_i)}} \\ & = E_{p(X=x_i)}\log{\frac{p(X=x_i)}{q(X=x_i)}} \end{align} \]

相对熵的性质

1. 如果\(p(x)\)和\(q(x)\)两个分布相同，那么相对熵等于0
2. \(DKL(p||q)≠DKL(q||p)\)，相对熵具有不对称性
3. \(DKL(p||q)≥0\)（利用Jensen不等式可证）

\[\begin{align} DKL(p||q) & = \sum_{i=1}^n p(X=x_i)\log{\frac{p(X=x_i)}{q(X=x_i)}} \\ & = - \sum_{i=1}^n p(X=x_i)\log{\frac{q(X=x_i)}{p(X=x_i)}} \\ & = - E_{p(X=x_i)}\log{\frac{q(X=x_i)}{p(X=x_i)}} \\ & \geq -\log{E_{p(X=x_i)}}\log{\frac{q(X=x_i)}{p(X=x_i)}} \\ & = - \log\sum_{i=1}^n p(X=x_i)\log{\frac{q(X=x_i)}{p(X=x_i)}} \\ & = - \log\sum_{i=1}^n q(X=x_i) \end{align} \]

其中\(\sum_{i=1}^n q(X=x_i)=1\)，得证\(DKL(p||q)≥0\)
4. 相对熵可以用来衡量两个概率分布之间的差异，上面公式的意义就是求\(p\)与\(q\)之间的对数差在\(p\)上的期望值

交叉熵（Cross Entropy）

  定义：基于相同时间测度的两个概率分布\(p(x)\)和\(q(x)\)的交叉熵是指，当基于一个“非自然”（相对于“真实分布”\(p(x)\)而言）的概率分布\(q(x)\)进行编码时，在时间集合中唯一标识一个事件所需要的平均比特数（使用非真实分布\(q(x)\)所指定的策略消除系统不确定性所需要付出的努力大小）。

  假设随机变量\(X\)可以取到\(n\)个值。现在有关于样本集的两个概率分布\(p(X=x_i)\)和\(q(X=x_i)\)，其中\(p(X=x_i)\)为真实分布，\(q(X=x_i)\)非真实分布。如果用真实分布\(p(X=x_i)\)来衡量识别别一个样本所需要编码长度的期望（平均编码长度）为:

\[\begin{align} H(p) & = \sum_{i=1}^n p(X=x_i)\log{\frac{1}{p(X=x_i)}} \\ & = - \sum_{i=1}^n p(X=x_i)\log{p(X=x_i)} \end{align} \]

  如果使用非真实分布\(q(X=x_i)\)来表示来自真实分布\(p(X=x_i)\)的平均编码长度，则是：

\[H(p,q) = \sum_{i=1}^n p(X=x_i)\log{\frac{1}{q(X=x_i)}} \]

  因为用\(q(X=x_i)\)来编码的样本来自于分布\(q(X=x_i)\)，所以\(H(p,q)\)中的概率是\(p(X=x_i)\)，此时就将\(H(p,q)\)称之为交叉熵。

  举个例子。考虑一个随机变量\(X\)，真实分布\(p(X)=({\frac{1}{2}},{\frac{1}{4}},{\frac{1}{8}},{\frac{1}{8}})\)，非真实分布\(q(X)=({\frac{1}{4}},{\frac{1}{4}},{\frac{1}{4}},{\frac{1}{4}})\)，则\(H(p)=1.75bits \text{最短平均码长}\)，交叉熵

\[H(p,q)={\frac{1}{2}}\log_24+{\frac{1}{4}}\log_24+{\frac{1}{8}}\log_24+{\frac{1}{8}}\log_24=2bits \]

由此可以看出根据非真实分布\(q(X=x_i)\)得到的平均码长大于根据真实分布\(p(X=x_i)\)得到的平均码长，但这种大于是个例还是总是会这样呢？

相对熵、交叉熵和熵的关系

  此处化简一下相对熵的公式。

\[\begin{align} DKL(p||q) & = \sum_{i=1}^np(X=x_i)\log{\frac{p(X=x_i)}{q(X=x_i)}} \\ & = \sum_{i=1}^np(X=x_i)\log{p(X=x_i)}−p(X=x_i)\log{q(X=x_i}) \end{align} \]

  如果此时联立熵的公式和交叉熵的公式

\[\begin{align} 熵 & = H(p) \\ & = −\sum_{i=1}^np(X=x_i)\log{p(X=x_i)} \end{align} \]

\[\begin{align} 交叉熵 & = H(p,q) \\ & = \sum_{i=1}^n p(X=x_i)\log{\frac{1}{q(X=x_i)}} \\ & = −\sum_{i=1}^np(X=x_i)\log{q(X=x_i)} \end{align} \]

即可推出

\[DKL(p||q)=H(p,q)−H(p) \]

  通过上述公式可以得出当用非真实分布\(q(x)\)得到的平均码长比真实分布\(p(x)\)得到的平均码长多出的比特数就是相对熵。

  又因为\(DKL(p||q)≥0\)，则\(H(p,q)≥H(p)\)，当\(p(x)=q(x)\)时，此时交叉熵等于熵。
  并且当\(H(p)\)为常量时（注：在机器学习中，训练数据分布是固定的），最小化相对熵\(DKL(p||q)\)等价于最小化交叉熵 \(H(p,q)\)也等价于最大化似然估计。

信息增益（Information Gain）

  假设有随机变量\((X,Y)\)，信息增益表示特征\(X\)的信息而使得类\(Y\)的信息不确定性减少的程度。

  特征\(A\)对训练集\(D\)的信息增益记作\(g(D,A)\)，则可以把该信息增益定义为集合\(D\)的经验熵与特征\(A\)给定条件下\(D\)的经验条件熵\(H(D|A)\)之差

\[g(D,A) = H(D) - H(D|A) \]

其中\(H(D)\)表示对数据集\(D\)进行分类的不确定性；\(H(D|A)\)表示在特征\(A\)给定的条件下对数据集\(D\)进行分类的不确定性；\(g(D,A)\)表示由于特征\(A\)而使得对数据集\(D\)的分类的不确定性减少的程度。因此可以发现对于数据集\(D\)而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益，信息增益大的特征具有更强的分类能力。

信息增益比（Information Gain Ratio）

  假设有随机变量\((X,Y)\)，特征\(A\)对数据集\(D\)的信息增益比记作\(g_R(D,A)\)，定义为

\[g_R(D,A) = {\frac{g(D,A)}{H_A(D)}} \]

其中特征熵\(H_A(D) = -\sum_{i=1}^n {\frac{D_i}{D}} \log_2 {\frac{D_i}{D}}\)，\(n\)是特征\(A\)的取值个数。

一张图带你看懂熵和信息增益

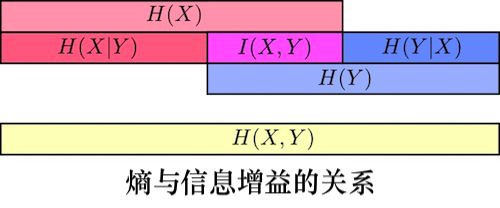
  假设有随机变量\((X,Y)\)，\(H(X)\)表示\(X\)的熵，\(H(Y)\)表示\(Y\)的熵，\(H(X|Y)\)表示已知\(Y\)时\(X\)的条件熵，\(H(Y|X)\)表示已知\(X\)时\(Y\)的条件熵，\(I(X,Y)\)表示信息增益，\(H(X,Y)\)表示的联合熵。