概率论-极大似然估计

目录

• 极大似然估计
• 最大似然原理
• 极大似然估计
• 似然函数
• 极大似然函数估计值
• 求解极大似然函数
  • 未知参数只有一个
  • 位置参数有多个
  • 总结

极大似然估计

最大似然原理

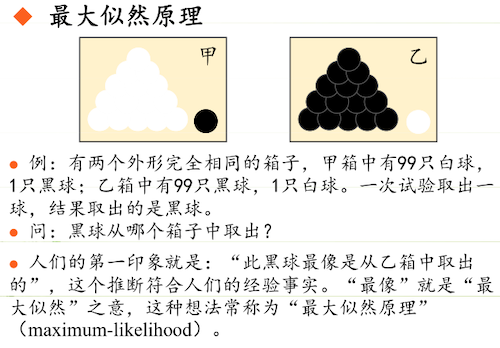
极大似然估计

  极大似然估计是建立在最大似然原理的基础上的一个统计方法。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即“模型已定，参数未知”。通过观察若干次实验的结果，利用实验结果得到某个参数值能够使样本出现的概率最大，则称为极大似然估计。

  简而言之，极大似然估计的目的是利用已知的样本结果，反推最有可能导致这样结果的参数值。

似然函数

  假设一个样本集\(D\)的\(n\)个样本都是独立同分布的，并且该样本集为

\[D={x_1,x_2,\ldots,x_n} \]

  似然函数（likelihood function）：联合概率密度函数\(p(D|\theta)\)称为相对于\({x_1,x_2,\ldots,x_n}\)的\(\theta\)的似然函数。

\[l(\theta) = p(D|\theta) = p(x_1,x_2,\ldots,x_n|\theta) = \prod_{i=1}^n p(x_i|\theta) \]

极大似然函数估计值

  如果\(\hat{\theta}\)是\(\theta\)参数空间中能使似然函数\(l(\theta)\)最大的\(\theta\)值，则\(\hat{\theta}\)是最可能的参数值，那么\(\hat{\theta}\)是\(\theta\)的最大似然估计量，记作

\[\hat{\theta} = d(x_1,x_2,\ldots,x_n) = d(D) \]

并且\(\hat{\theta}(x_1,x_2,\ldots,x_n)\)称作极大似然函数估计值。

求解极大似然函数

  给出求解最大\(\theta\)值的公式

\[\hat{\theta} = arg \underbrace{max}_\theta l(\theta) = arg \underbrace{max}_\theta \prod_{i=1}^n p(x_i|\theta) \]

  为了方便计算，定义对数似然函数\(H(\theta)\)，即对似然函数求对数

\[H(\theta) = \ln{l(\theta)} \]

  因此求最大\(\theta\)值的公式变成了

\[\hat{\theta} = arg \underbrace{max}_\theta H(\theta) = arg \underbrace{max}_\theta \ln{l(\theta)} = arg \underbrace{max}_\theta \prod_{i=1}^n \ln{p(x_i|\theta)} \]

并且可以发现公式中只有一个变量\(\theta\)

未知参数只有一个

  如果\(\theta\)为标量，在似然函数满足连续、可微的情况下，则极大似然估计量是下面微分方程的解

\[{\frac{dH(\theta)}{d\theta}} = {\frac{d\ln{l(\theta)}}{d\theta}} = 0 \]

位置参数有多个

  如果\(\theta\)为\(k\)维向量，可以把\(\theta\)记作\(\theta = [\theta_1,\theta_2,\ldots,\theta_k]^T\)，对\(\theta_1,\theta_2,\ldots,\theta_k\)求梯度，可得

\[\Delta_\theta=[{\frac{\partial}{\partial_{\theta_1}}},{\frac{\partial}{\partial_{\theta_2}}},\cdots,{\frac{\partial}{\partial_{\theta_s}}}]^T \]

  如果似然函数满足连续、可导的情况下，则最大似然估计量就是如下方程的解：

\[\Delta_\theta{H(\theta)} = \Delta_\theta\ln{l(\theta)} = \sum_{i=1}^n \Delta_\theta \ln(p(x_i|\theta)) = 0 \]

总结

  方程的解只是一个估计值，只有在样本趋于无限多的时候，才会逐渐接近真实值。