概率论-常见的概率分布模型

常见的概率分布模型

离散概率分布函数

  离散概率分布也称为概率质量函数（probability mass function），离散概率分布的例子有

    伯努利分布（Bernoulli distribution）

    二项分布（binomial distribution）

    泊松分布（Poisson distribution）

    几何分布（geometric distribution）等

连续概率分布函数

  连续概率分布也称为概率密度函数（probability density function），它们是具有连续取值（例如一条实线上的值）的函数，连续概率分布的例子有

    正态分布（normal distribution）

    指数分布（exponential distribution）

    β分布（beta distribution）等

联合分布函数

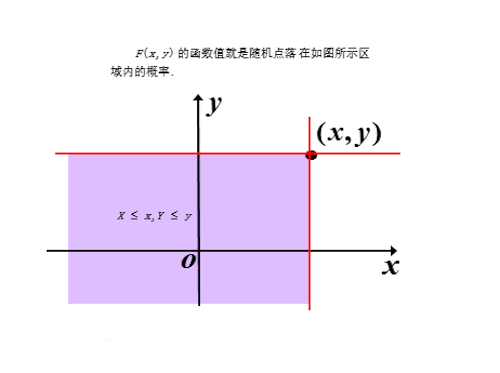
  给定一个随机变量\((X,Y)\)，称定义域为整个平面的二元实值函数

\[F(x,y) = P(X\leq{x},Y\leq{y}) \quad -\infty\geq{x,y}\leq\infty \]

该二元实值函数为随机变量\((X,Y)\)的分布函数，也可以称为是\((X,Y)\)的联合分布函数。

  按照联合分布函数的定义，\(F(x,y)=P((X,Y)\in{D_{xy}})\)，其中\(D_{xy}\)如下图所示

多项分布（Multinomial Distribution）

多项分布简介

  多项分布是二项分布的推广，他们的区别是二项分布的结果只有\(0\)和\(1\)两种，多项式的结果可以有多个值。

  多项分布的典型例子是掷骰子，6个点对应6个不同的数，每个点的概率都为\({\frac{1}{6}}\)

  与二项分布类似，多项分布来自于\((p_1+p_2+\cdots+p_k)^n多项式的展开\)

多项分布公式解析

  以掷骰子为例，掷骰子的时候掷\(1-6\)的概率都为\({\frac{1}{6}}\)，记作\(p_1-p_6\)，可以发现\(p_1+p_2+p_3+p_4+p_5+p_6=1\)，现在把\(p_1+p_2+p_3+p_4+p_5+p_6\)记作做一次抽样各种事件发生的概率和，即可得\((p_1+p_2+p_3+p_4+p_5+p_6)^n=1^n\)为\(n\)次抽样所有事件相互组合对应的概率和，之后使用多项式展开(注：使用多项式定理展开，由于多项式定理不在本节提及范围内，不多赘述)，如果它不是掷骰子，而是一个有\(n\)种可能的问题，会得到一个多项式展开的公式

\[P(X_1 = x_1,\ldots,X_k = x_k) = \begin{cases} {\frac{n!}{x_1!\cdots{x_k!}}}(p^{x_1}\cdots{p^{x_k})} \quad when\sum_{i=1}^kx_i=n\\ 0 \quad otherwise \\ \end{cases} \]

这个多项式表示\(X_1\)出现\(x_1\)次，\(X_2\)出现\(x_2\)次，\(\ldots\)，\(X_k\)出现\(x_k\)次的出现概率，这样就得到了上述所示的多项分布的多项展开式公式。

伯努利分布（Bernoulli Distribution）

伯努利分布简介

  伯努利分布是一个二值离散分布，结果只有\(0\)和\(1\)两种。

  随即变量\(X\)为\(1\)的概率为\(p\)，则为\(0\)的概率为\(q=1-p\)，可以用公式表示为

\[f(x) = p^x(1-p)^{1-x} = \begin{cases} p, \quad\quad x=1 \\ 1-p, \quad x=0 \\ \end{cases} \]

伯努利分布的期望值和方差

  伯努利分布的期望值为

\[\begin{align} E(X) & = \sum_{i=0}^1x_if(x) \\ & = 1*p+0*(1-p) \\ & = p+0 \\ & = p \\ \end{align} \]

  伯努利分布的方差为

\[\begin{align} D(x) & = \sum_{i=0}^1(x_i - E(x))^2f(x) \\ & = (1-E(x))^2*p + (0-E(x)^2*(1-p) \\ & = (1-p)^2*p + (0-p)^2*(1-p) \\ & = p - p^2 \\ & = p(1-p) \\ & = pq \end{align} \]

正态(高斯)分布（Normal(Gaussian) Distribution）

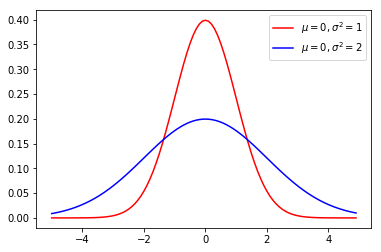
正态分布的概率密度函数图像

  其中红线表示的是标准正态分布图像。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline

mu1 = 0
sig1 = 1
mu2 = 0
sig2 = 2

x = np.arange(-5, 5, 0.1)
y1 = stats.norm.pdf(x, mu1, sig1)
y2 = stats.norm.pdf(x, mu2, sig2)
plt.plot(x, y1, 'r-', label='$\mu=0,\sigma^2=1$')
plt.plot(x, y2, 'b-', label='$\mu=0,\sigma^2=2$')
plt.legend()
plt.show()

正态分布简介

  正态分布也称作高斯分布，是最常见的一种分布，其概率密度函数为

\[f(x;\mu,\sigma) = {\frac {1} {\sqrt{2\pi\sigma^2}} } e^{(-{\frac {(x - \mu)^2} {2\sigma^2}})} \]

  如果一个随即变量\(X\)服从该分布，可以写作\(X ~ { N(\mu ,\sigma ^{2})} N(\mu, \sigma^2)\)。

  当\(\mu=0,\sigma=1\)时的正态分布称作标准正态分布，这个分布能简化为

\[f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right) \]

  标准正态分布曲线区间面积计算

\[f(|x-\mu|<\sigma) = 0.6826 \\ f(|x-\mu|<2\sigma) = 0.9544 \\ f(|x-\mu|<3\sigma) = 0.9974 \\ \]

中心极限定理与正态分布

1. 中心极限定理1：把许多未知的小作用加起来看作一个变量，这个变量服从正态分布
2. 中心极限定理2：“大量统计独立的随即变量的和”的分布趋于正态分布

泊松分布（Poisson Distribution）

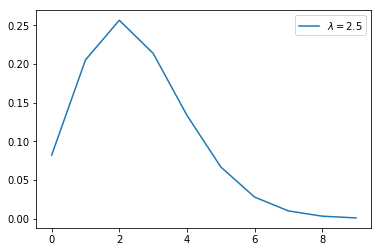
泊松分布的概率质量函数图像

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline

lambd = 2.5

x = np.arange(0, 10)
y = stats.poisson.pmf(x, lambd)
plt.plot(x, y, label='$\lambda=2.5$')
plt.legend()
plt.show()

二项分布（Binomial Distributio）

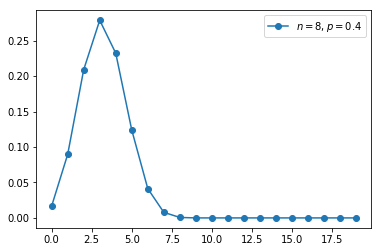
二项分布的概率质量函数图像

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline

n = 8
p = 0.4

x = np.arange(0, 20)
y = stats.binom.pmf(x, n, p)
plt.plot(x, y, 'o-', label='$n=8,p=0.4$')
plt.legend()
plt.show()

二项分布简介

  二项分布是\(n\)次独立的二值实验(伯努利实验)中成功的次数的离散值概率分布(\(n\)次伯努利实验，一次伯努利实验得到一个伯努利分布)。

  随机变量\(X\)服从参数\(n\)和\(p\)的二项分布记作：\(B(n,p)\)。\(n\)次实验中\(k\)次成功的概率质量函数为

\[f(k;n,p) = C_n^kp^k(1-p)^{n-k} \]

其中\(C_n^k\)是二项式系数：\(C_n^k = {\frac{n!}{k!(n-k)!}}\)

  二项分布来源于牛顿二项式

\[(a+b)^n = \sum_{k=0}^nC_n^ka^kb^{n-k} \]

二项分布与伯努利分布

1. 二项分布的期望是伯努利分布期望的\(n\)倍

\[E(x) = np \]

2. 二项分布的方差是伯努利分布方差的\(n\)倍

\[D(x) = np(1-p) \]

贝塔分布（Beta Distribution）

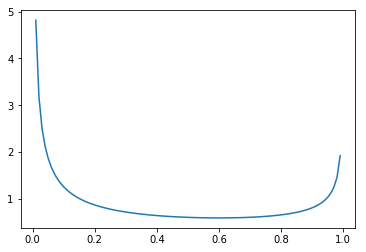
贝塔分布的概率密度函数图像

from scipy import stats
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

a = 0.4
b = 0.6

x = np.arange(0.01, 1, 0.01)
y = stats.beta.pdf(x, a, b)
plt.plot(x, y, label='a=0.4,b=0.6')
plt.show()

几何分布(负二项分布)（Geometric Distribution）

几何分布概率质量函数图像

狄利克雷分布(多项分布的共轭分布)（Dirichlet distribution）

超几何分布（Hypergeometric Distribution）

指数分布（Exponential Distribution）

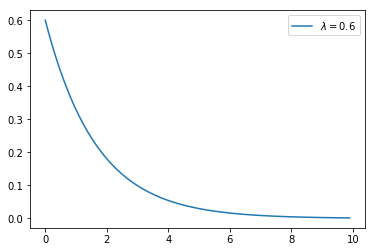
指数分布概率密度函数图像

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline

lambd = 0.6

x = np.arange(0, 10, 0.1)
y = lambd * np.exp(-lambd*x)
plt.plot(x, y, label='$\lambda=0.6$')
plt.legend()
plt.show()