08-06 细分构建机器学习应用程序的流程-数据预处理
目录
细分构建机器学习应用程序的流程-数据预处理
sklearn数据预处理官方文档地址：https://scikit-learn.org/stable/modules/classes.html#module-sklearn.preprocessing
1.1 缺失值处理
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn import datasets
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
现实生活中的数据往往是不全面的，很多样本的属性值会有缺失，例如某个人填写的个人信息不完整或者对个人隐私的保护政策导致建模时可能无法得到所需要的特征，尤其是在数据量较大时，这种缺失值的产生会对模型的性能造成很大的影响。接下来将通过鸢尾花数据讨论缺失值处理的方法。
# 缺失值处理示例
from io import StringIO
iris_data = '''
5.1,,1.4,0.2
4.9,3.0,1.4,0.2
4.7,3.2,,0.2
7.0,3.2,4.7,1.4
6.4,3.2,4.5,1.5
6.9,3.1,4.9,
,,,
'''
iris = datasets.load_iris()
df = pd.read_csv(StringIO(iris_data), header=None)
df.columns = iris.feature_names
df = df.iloc[:, :4]
df
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | NaN | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | NaN | 0.2 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 |
| 5 | 6.9 | 3.1 | 4.9 | NaN |
| 6 | NaN | NaN | NaN | NaN |
1.1.1 删除缺失值
# axis=0删除有NaN值的行，axis=1删除有NaN值的列
df.dropna(axis=0)
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 |
# 删除全为NaN值得行或列
df.dropna(how='all')
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | NaN | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | NaN | 0.2 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 |
| 5 | 6.9 | 3.1 | 4.9 | NaN |
# 删除行不为4个值的
df.dropna(thresh=4)
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 |
# 删除花萼长度中有NaN值的数据
df.dropna(subset=['sepal length (cm)'])
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | NaN | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | NaN | 0.2 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 |
| 5 | 6.9 | 3.1 | 4.9 | NaN |
4.6.1.2 填充缺失值
# 填充缺失值示例
from sklearn.impute import SimpleImputer
# 对所有缺失值填充固定值0
# imputer = SimpleImputer(missing_values=np.nan, strategy='constant', fill_value=0)
# 中位数strategy=median，众数strategy=most_frequent
imputer = SimpleImputer(missing_values=np.nan, strategy='mean')
imputer = imputer.fit_transform(df.values)
df = pd.DataFrame(imputer, columns=iris.feature_names)
df
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | 0.0 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 0.0 | 0.2 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 |
| 5 | 6.9 | 3.1 | 4.9 | 0.0 |
| 6 | 0.0 | 0.0 | 0.0 | 0.0 |
1.2 异常值处理
异常值有时候也会被称为离群值，处理异常值的方式类似于缺失值处理，可以暴力删除，也可以填充。但是异常值往往需要手动获取，一般获取异常值的方式有以下两种：
-
统计分析原则
对特征值统计后分析判断哪些值是不符合逻辑的，拿年龄举例，如果发现某个人的年龄是200，至少目前是不合理的，因此可以设定一个条件，把年龄大于200的数据都排除掉。
-
概率分布原则
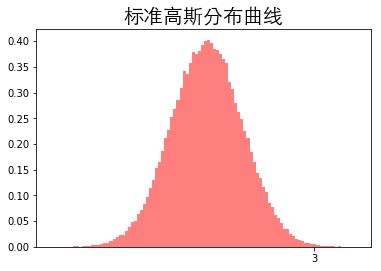
根据高斯分布可知距离平均值\(3\delta\)之外的概率为0.003，这在统计学中属于极小概率事件，因此可以把超过该距离的值当作异常值处理。当然，你也可以手动设定这个距离或概率，具体问题具体分析。
# 标准高斯分布曲线
fig, ax = plt.subplots()
np.random.seed(1)
# 创建一组平均数为0，标准差δ为1，总个数为100000的符合标准正态分布的数据
Gaussian = np.random.normal(0, 1, 100000)
ax.hist(Gaussian, bins=100, histtype="stepfilled",
density=True, alpha=0.5, color='r')
plt.xticks(np.arange(3, 4))
plt.title('标准高斯分布曲线', fontproperties=font, fontsize=20)
plt.show()
1.3 自定义数据类型编码
现有一个汽车样本集，通过这个汽车样本集可以判断人们是否会购买该汽车。但是这个样本集的特征值是离散型的，为了确保计算机能正确读取该离散值的特征，需要给这些特征做编码处理，即创建一个映射表。如果特征值分类较少，可以选择自定义一个字典存放特征值与自定义值的关系。接下来将直接通过scikit-learn库转换属性值类型。
# 汽车样本
car_data = '''
乘坐人数,后备箱大小,安全性,是否可以接受
4,med,high,acc
2,big,low,unacc
4,big,med,acc
4,big,high,acc
6,small,low,unacc
6,small,med,unacc
'''
df = pd.read_csv(StringIO(car_data), header=0)
df
| 乘坐人数 | 后备箱大小 | 安全性 | 是否可以接受 | |
|---|---|---|---|---|
| 0 | 4 | med | high | acc |
| 1 | 2 | big | low | unacc |
| 2 | 4 | big | med | acc |
| 3 | 4 | big | high | acc |
| 4 | 6 | small | low | unacc |
| 5 | 6 | small | med | unacc |
safety_mapping = {
'low': 0,
'med': 1,
'high': 2,
}
df['安全性'] = df['安全性'].map(safety_mapping)
df
| 乘坐人数 | 后备箱大小 | 安全性 | 是否可以接受 | |
|---|---|---|---|---|
| 0 | 4 | med | 2 | acc |
| 1 | 2 | big | 0 | unacc |
| 2 | 4 | big | 1 | acc |
| 3 | 4 | big | 2 | acc |
| 4 | 6 | small | 0 | unacc |
| 5 | 6 | small | 1 | unacc |
# 对上述字典做反向映射处理，即反向映射回原来的离散类型的特征值。
inverse_safety_mapping = {v: k for k, v in safety_mapping.items()}
df['安全性'].map(inverse_safety_mapping)
0 high
1 low
2 med
3 high
4 low
5 med
Name: 安全性, dtype: object
1.4 通过sklearn对数据类型编码
继续沿用上一个汽车样本，使用sklearn自带库对数据类型编码。
# scikit-learn数据类型编码示例
from sklearn.preprocessing import LabelEncoder
X_label_encoder = LabelEncoder()
X = df[['乘坐人数', '后备箱大小', '安全性']].values
X[:, 1] = X_label_encoder.fit_transform(X[:, 1])
X
array([[4, 1, 2],
[2, 0, 0],
[4, 0, 1],
[4, 0, 2],
[6, 2, 0],
[6, 2, 1]], dtype=object)
# 对标记进行编码
y_label_encoder = LabelEncoder()
y = y_label_encoder.fit_transform(df['是否可以接受'].values)
y
array([0, 1, 0, 0, 1, 1])
# 对标记反向映射回原始数据
y_label_encoder.inverse_transform(y)
array(['acc', 'unacc', 'acc', 'acc', 'unacc', 'unacc'], dtype=object)
1.5 独热编码
假设汽车安全性只是一个衡量标准，没有特定的顺序。但是计算机很有可能把这些\(0,1,2\)作一个特定排序或者因此区分它们的重要性，这个时候就得考虑创建一个二进制值分别表示low、med、high这三个属性值，有为1，没有为0，例如\(010\)表示为med。
1.5.1 sklearn做独热编码
# 独热编码示例
from sklearn.preprocessing import OneHotEncoder
one_hot_encoder = OneHotEncoder(categories='auto')
one_hot_encoder.fit_transform(X).toarray()
array([[0., 1., 0., 0., 1., 0., 0., 0., 1.],
[1., 0., 0., 1., 0., 0., 1., 0., 0.],
[0., 1., 0., 1., 0., 0., 0., 1., 0.],
[0., 1., 0., 1., 0., 0., 0., 0., 1.],
[0., 0., 1., 0., 0., 1., 1., 0., 0.],
[0., 0., 1., 0., 0., 1., 0., 1., 0.]])
1.5.2 pandas做独热编码
# 使用pandas对数据做独热编码处理，数值型数据不做编码处理
pd.get_dummies(df[['乘坐人数', '后备箱大小', '安全性']])
| 乘坐人数 | 安全性 | 后备箱大小_big | 后备箱大小_med | 后备箱大小_small | |
|---|---|---|---|---|---|
| 0 | 4 | 2 | 0 | 1 | 0 |
| 1 | 2 | 0 | 1 | 0 | 0 |
| 2 | 4 | 1 | 1 | 0 | 0 |
| 3 | 4 | 2 | 1 | 0 | 0 |
| 4 | 6 | 0 | 0 | 0 | 1 |
| 5 | 6 | 1 | 0 | 0 | 1 |
使用独热编码在解决特征值无序性的同时也增加了特征数，这无疑会给未来的计算增加难度，因此可以适当减少不必要的维度。例如当为后备箱进行独热编码的时候会有后备箱大小_big、后备箱大小_med、后备箱大小_small三个特征，可以减去一个特征，即后备箱大小_big与后备箱大小_med都为0则代表是后备箱大小_small。在调用pandas的get_dummies函数时，可以添加drop_first=True参数；而使用OneHotEncoder时得自己分隔。
pd.get_dummies(df[['乘坐人数', '后备箱大小', '安全性']], drop_first=True)
| 乘坐人数 | 安全性 | 后备箱大小_med | 后备箱大小_small | |
|---|---|---|---|---|
| 0 | 4 | 2 | 1 | 0 |
| 1 | 2 | 0 | 0 | 0 |
| 2 | 4 | 1 | 0 | 0 |
| 3 | 4 | 2 | 0 | 0 |
| 4 | 6 | 0 | 0 | 1 |
| 5 | 6 | 1 | 0 | 1 |
1.6 数据标准化
1.6.1 最小-最大标准化
为了解决相同权重特征不同尺度的问题，可以使用机器学习中的最小-最大标准化做处理，把他们两个值压缩在\([0-1]\)区间内。
最小-最大标准化公式：
\[x_{norm}^{(i)}={\frac{x^{(i)}-x_{min}}{x_{max}-x_{min}}}
\]
其中\(i=1,2,\cdots,m\)；\(m\)为样本个数；\(x_{min},x_{max}\)分别是某个的特征最小值和最大值。
# 最小最大标准化示例
from sklearn.preprocessing import MinMaxScaler
import numpy as np
test_data = np.array([1, 2, 3, 4, 5]).reshape(-1, 1).astype(float)
min_max_scaler = MinMaxScaler()
min_max_scaler.fit_transform(test_data)
array([[0. ],
[0.25],
[0.5 ],
[0.75],
[1. ]])
1.6.2 Z-score标准化
Z-score标准化方法也可以对数据进行标准化，但是它的标准化并不能把数据限制在某个区间，它把数据压缩成类似高斯分布的分布方式，并且也能处理离群值对数据的影响。
在分类、聚类算法中，需要使用距离来度量相似性的时候应用非常好，尤其是数据本身呈正态分布的时候。
数据标准化公式：
\[x_{std}^{(i)}={\frac{x^{(i)}-\mu{_x}}{\sigma{_x}}}
\]
使用标准化后，可以把特征列的中心设在均值为\(0\)且标准差为\(1\)的位置，即数据处理后特征列符合标准正态分布。
# Z-score标准化
from sklearn.preprocessing import StandardScaler
test_data = np.array([1, 2, 3, 4, 5]).reshape(-1, 1).astype(float)
standard_scaler = StandardScaler()
# fit_transform()=fit()+transform(), fit()方法估算平均值和方差，transform()方法对数据标准化
standard_scaler.fit_transform(test_data)
array([[-1.41421356],
[-0.70710678],
[ 0. ],
[ 0.70710678],
[ 1.41421356]])
1.7 二值化数据
二值化数据类似于独热编码，但是不同于独热编码的是它不是0就是1，即又有点类似于二分类。直接给出数据二值化的公式：
\[y = \begin{cases}
0,\quad if x \leq {\theta} \\
1,\quad if x \geq {\theta}
\end{cases}
\]
其中\(\theta\)是手动设置的阈值，如果特征值小于阈值为0；特征值大于阈值为1。
# 数据二值化示例
from sklearn.preprocessing import Binarizer
test_data = np.array([1, 2, 3, 4, 5]).reshape(-1, 1).astype(float)
binarizer = Binarizer(threshold=2.5)
binarizer.fit_transform(test_data)
array([[0.],
[0.],
[1.],
[1.],
[1.]])
1.8 正则化数据
正则化是将每个样本缩放到单位范数，即使得每个样本的p范数为1，对需要计算样本间相似度有很大的作用，通常有L1正则化和L2正则化两种方法。
# L1正则化示例
from sklearn.preprocessing import normalize
test_data = [[1, 2, 0, 4, 5], [2, 3, 4, 5, 9]]
normalize = normalize(test_data, norm='l1')
normalize
array([[0.08333333, 0.16666667, 0. , 0.33333333, 0.41666667],
[0.08695652, 0.13043478, 0.17391304, 0.2173913 , 0.39130435]])
# L2正则化示例
from sklearn.preprocessing import Normalizer
test_data = [[1, 2, 0, 4, 5], [2, 3, 4, 5, 9]]
normalize = Normalizer(norm='l2')
normalize = normalize.fit_transform(test_data)
normalize
array([[0.14744196, 0.29488391, 0. , 0.58976782, 0.73720978],
[0.17213259, 0.25819889, 0.34426519, 0.43033148, 0.77459667]])
1.9 生成多项式特征
# 生成多项式特征图例
import matplotlib.pyplot as plt
from sklearn import datasets
%matplotlib inline
X1, y1 = datasets.make_circles(
n_samples=1000, random_state=1, factor=0.5, noise=0.1)
plt.scatter(0, 0, s=23000, color='white', edgecolors='r')
plt.scatter(X1[:, 0], X1[:, 1], marker='*', c=y1)
plt.xlabel('$x_1$', fontsize=15)
plt.ylabel('$x_2$', fontsize=15)
plt.title('make_circles()', fontsize=20)
plt.show()
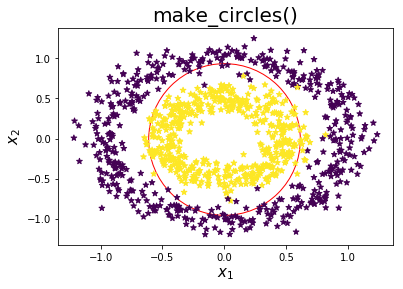
有时候可能会遇到上图所示的数据分布情况，如果这个时候使用简单的\(x_1,x_2\)特征去拟合曲线，明显是不可能的，但是我们可以使用，但是我们可以使用\(x_1^2+x_2^2=1\)去拟合数据，可能会得到一个较好的模型，所以我们有时候会对特征做一个多项式处理，即把特征\(x_1,x_2\)变成\(x_1^2,x_2^2\)。
test_data = [[1, 2], [3, 4], [5, 6]]
test_data
[[1, 2], [3, 4], [5, 6]]
通过多项式特征，特征将会做如下变换
\[x_1,x_2\quad\rightarrow\quad1,x_1,x_2,x_1^2,x_1x_2,x_2^2
\]
# 生成多项式特征示例
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures()
poly = poly.fit_transform(test_data)
poly
array([[ 1., 1., 2., 1., 2., 4.],
[ 1., 3., 4., 9., 12., 16.],
[ 1., 5., 6., 25., 30., 36.]])
