06-01 DeepLearning-图像识别

深度学习-图像识别

人脸定位

  相信你们外出游玩的时候，都不会带上你的牛逼plus诺基亚手机出门，而是带上你的智能手机给自己美美的拍上一张。当你用手机镜头对准人脸的时候，都会出现一个矩形框，如下图所示（前方高能），那么这个技术是怎么做到的呢？

  相机中的人脸定位技术用的是二分类技术。该技术流程如下图所示。

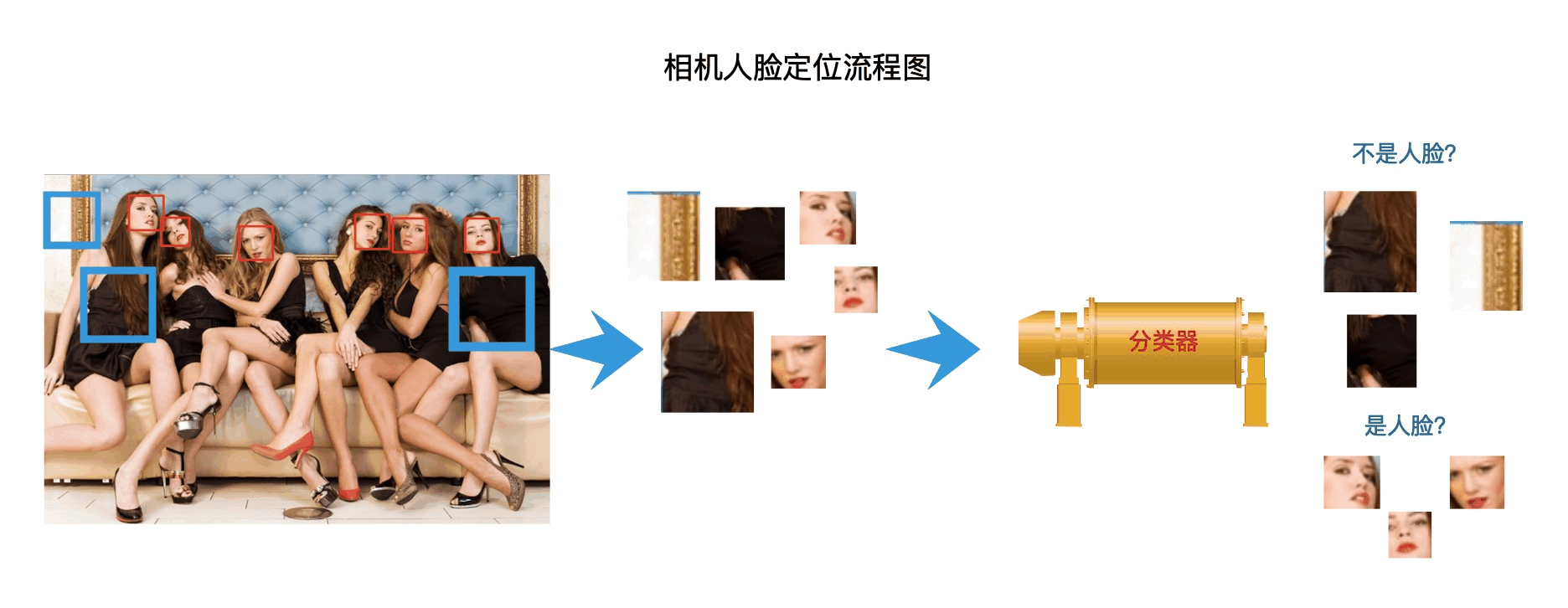
  如上图所示，相机首先会将照片分割成一块块的图像块，一张照片往往会有成千上万的图像块被切割出来。

  然后每一个图像块都会经过人脸分类器去判别是否是人脸。人脸分类器是预先训练好的分类器，类似于我们之前讲的手写数字识别应用程序中的支持向量机分类器。如果人脸分类器预测该图像块为人脸，相机则会在这个图像块中显示出框的位置。

  在人脸定位中，为了解决由于手机离人的距离不同，导致手机上显示的人脸大小不一致的问题。手机在切割图像的时候，并不是只用一种尺寸的图像块切割图像，而是有从小到大很多尺寸的图像块，因此保证了图像块切割图像时能涵盖几乎各种大小的人脸。

  由于相机使用不同尺寸的图像块判别图像块是否为人脸，因此会导致不同尺寸、不同位置的图像块可能同时都被判别为是人脸，因此会有很多重叠框。对于该问题，通常在后期使用后处理融合技术，将这些框融合为一个框。

手工提取特征的图像分类

识图认物

  在我国古代的时候，人们就对识图认物有了一定的认知。《史记》中曾记载：赵高指鹿为马；《艾子杂说》中记载：有人欲以鹘（hú，鹰属猛禽）猎兔而不识鹘，买凫（fú，鸭子）而去，逼凫捉兔，成为笑谈。

  如今千年之后深度学习技术，可以让避免让我们成为识物盲？

传统分类系统的特征提取

  曾经讲到鸢尾花分类的时候，我们给出了分类任务的两个核心步骤：特征提取和特征分类。如下图所示。

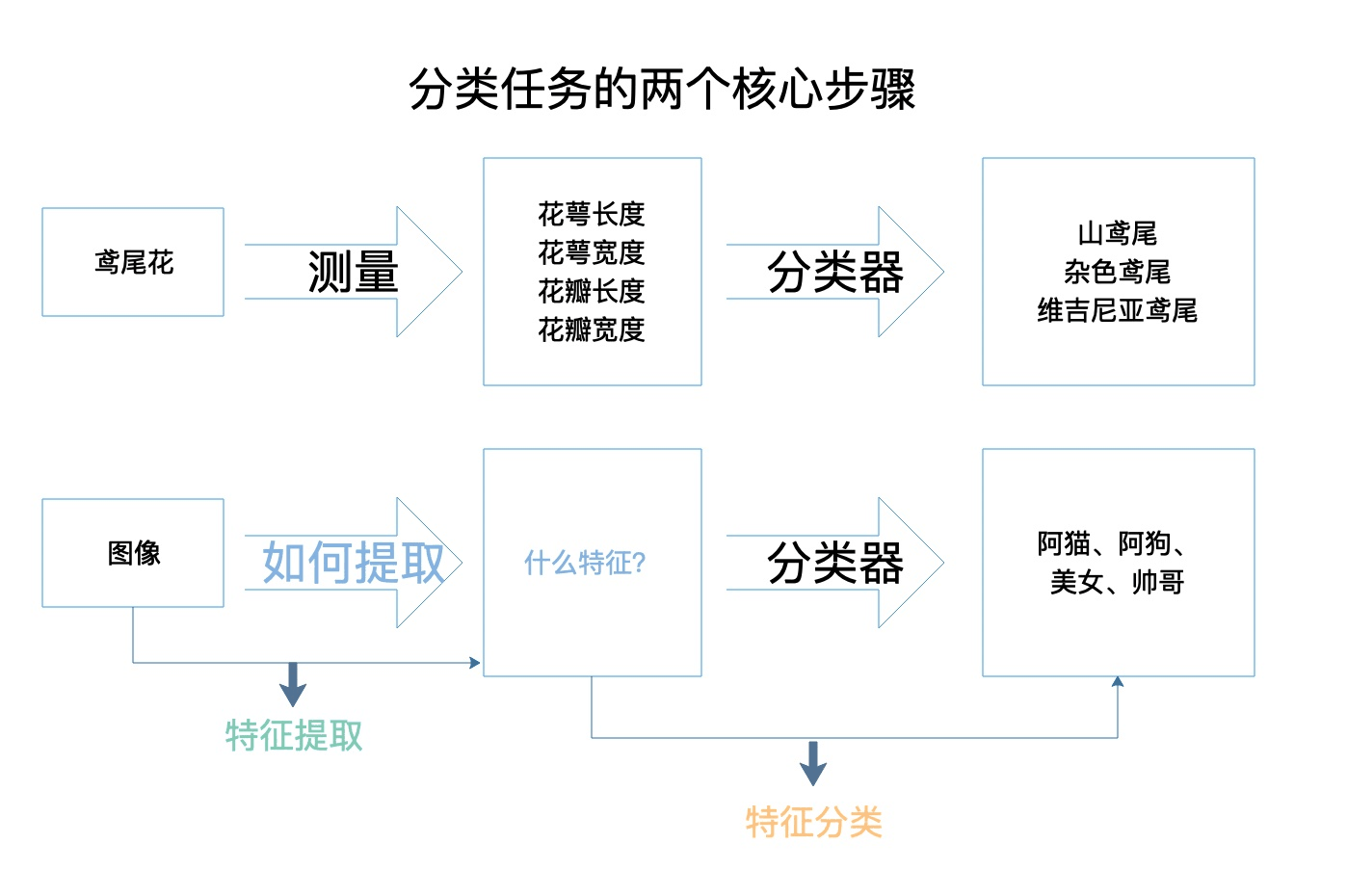
  上图我们为了减少麻烦，所以我也直接给出了手工提取特征的图像分类的过程，从图中可以看出在图像分类过程中，我们主要停滞在了特征提取的步骤，我们该如何提取图像的特征，提取什么特征呢？如果要解决上述问题，我们首先需要把自己看成计算机去看图像。

计算机眼中的图像

  图像在计算机中的表示如下图所示。

  如上图所示，如果将一副计算机眼中的图放大，我们可以看到一幅图像在计算机眼中就是一个由数字组成的矩形阵列，即矩阵，也正是如此图像才可以存储在计算机中。对于矩阵内的每一个元素，我们称之为像素；而矩阵的行数和列数，我们称为分辨率。我们经常说的1280×720分辨率，值得就是这张图由1280行、720列的像素组成的。反之，如果我们给出一个数字组成的矩阵，然后将矩阵中的每个元素转换为对应的颜色后，并在电脑屏幕上显示出来，既可以复原出这张图像。

  细心的同学会发现矩阵中的每个元素都是介于0-255之间的整数。对于上图所示的黑白图像，由于只有明暗的区别，因此只需要一个数字就可以表示不同的灰度，通常我们使用0表示最暗的黑色，255表示最亮的白色，所以矩阵的每一个元素都是介于0-255之间的整数。

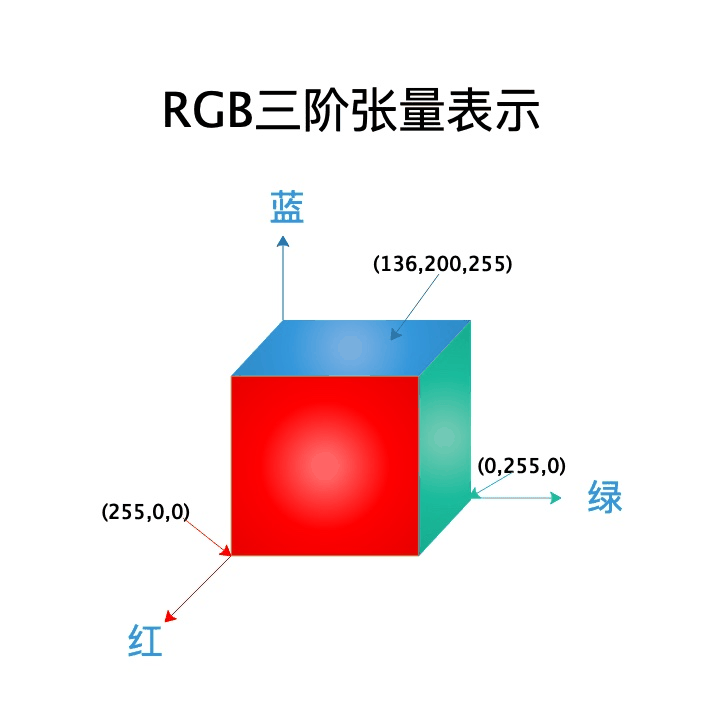
  如上图所示，现在我们最常看到的是彩色图像，彩色图像由于使用（R，G，B）三个数字表示一个颜色，他表示用红（R），绿（G），蓝（B）三种基本颜色叠加的颜色，并且三种颜色也都是介于0-255之间的整数。由于使用三种基本颜色叠加成颜色的明亮程度，如（255，0，0）表示纯红色、（136，200，255）表示天蓝色，所以一般一张彩色图像，需要使用一个由整数的立方体阵列来表示，这样的立方体阵列我们称之为三阶张量。这个三阶张量的长度与宽度即为图像的分辨率，高度为3。对于黑白图像，他其实是高度为1的三阶张量。

什么是图像特征？

  如今我们已经了解了计算机眼中的图像，但是仅仅了解了图像并没有用。如果现在在你眼前有猫、小鸟和树叶，我们可以想想，我们人类是如何对图片分类的。

  通过上图，我们很容易得出下表，通过“有没有翅膀”和“有没有眼睛”这两个特征对猫、鸟、和树叶分类。如：没有翅膀有眼睛的是猫、有翅膀又有眼睛的是鸟、没有翅膀没有眼睛的是树叶。

特征	猫	鸟	树叶
有没有翅膀	没有	有	没有
有没有眼睛	有	有	没有

  由于图像在计算机眼中是一个三阶张量的东西（黑白图像是特殊的三阶张量），所以计算机并不知道图像中的物体有没有翅膀、有没有眼睛。很早之前为了让计算机认识翅膀、认识眼睛，人们通常手工设计各种图像特征，如：设计翅膀图画的颜色、边缘、纹理等性质，然后结合机器学习技术，达到物体识别的目的。

  由于图像在计算机眼中可以表示为三阶张量，从图像中提取特征，即对这个三阶张量进行运算的过程。其中我们最常用的运算是卷积。

卷积运算

  卷积运算目前在图像处理中有着广泛的应用，他如我们熟知的加减乘除一样也是一种数学运算。只是参加卷积运算的是向量、矩阵或三阶张量。

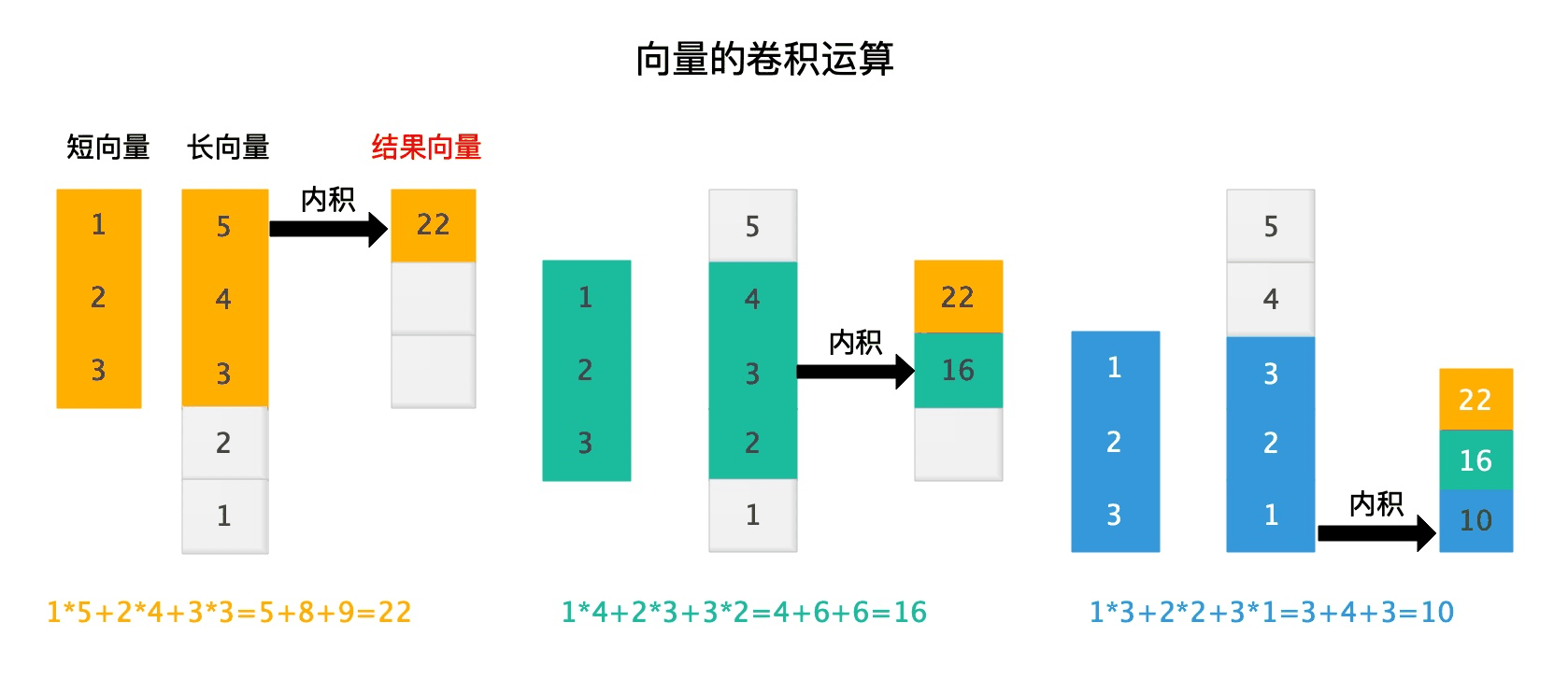
  如上图所示，两个向量的卷积仍然是一个向量。他的计算过程如上图所示：

1. 我们首先将两个向量的第一个元素对齐，并截去长向量中多于的元素，然后计算这两个维数相同的向量的内积，并将算得的结果作为结果向量的第一个元素。
2. 我们将短向量向下滑动一个元素，从长向量中截去不能与之对应的元素，并计算内积作为结果向量的第二个元素。
3. 重复“滑动-截取-计算内积”这个过程，直到短向量的最后一个元素与长向量的最后一个元素对齐为止。

  卷积结果的维数通常比长向量低，因此有时候我们为了使得卷积后的结果向量与原始长向量的长度一直，会在长向量的两端补上一些0.对于如上图所示的长向量\((5,4,3,2,1)\)，我们可以将其两端补零变成\((0,5,4,3,2,1,0)\)，之后再进行卷积运算，得到结果向量为\((0,22,16,10,0)\)。

  通过向量的卷积运算，我们可以定义矩阵的卷积运算，对于两个形状相同的矩阵，他们的内积是每个对应位置的数字相乘之后的和，如下图所示。

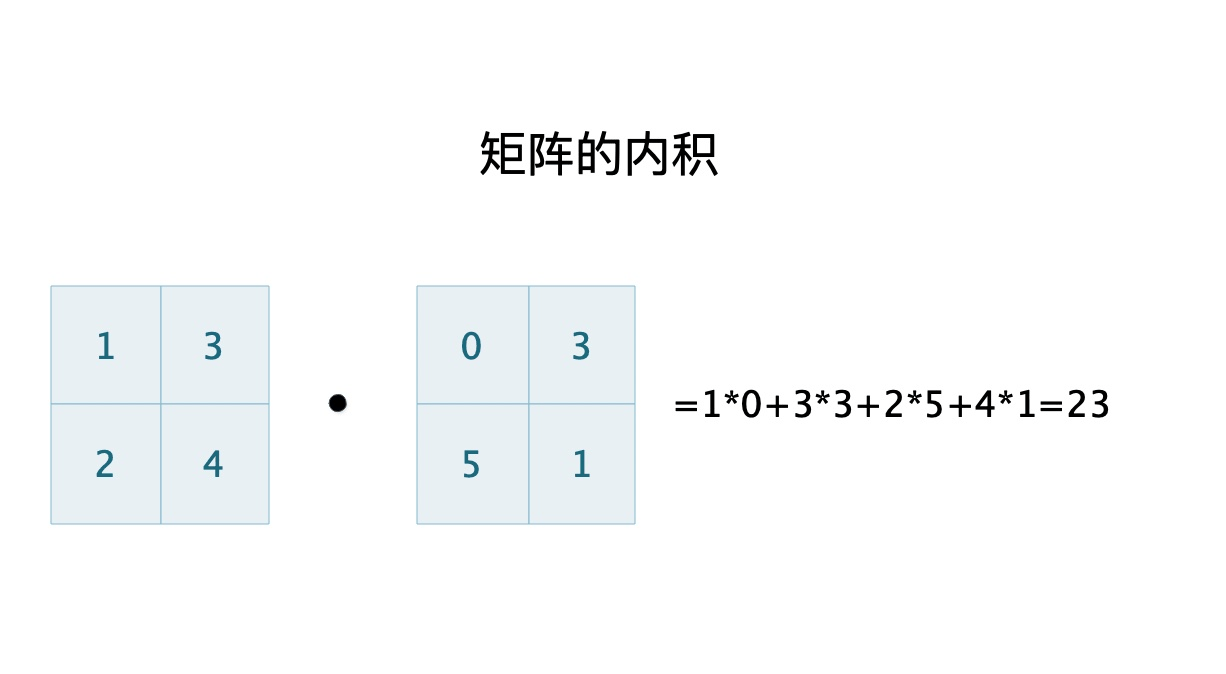
  进行向量的卷积时，我们只需要朝着一个方向移动；进行矩阵卷积时，我们通常需要沿着横向和纵向两个方向滑动，如下图所示。

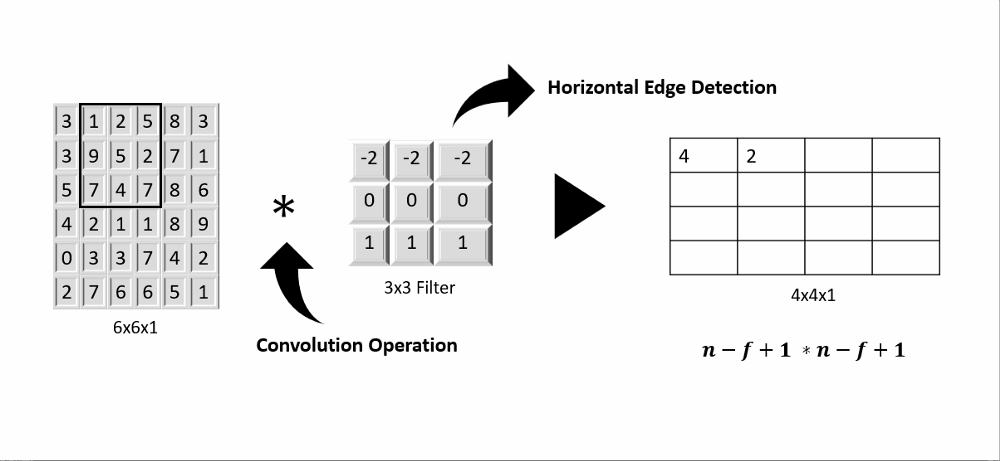
  定义矩阵的卷积之后，类似的也可以定义三阶张量的卷积，如下图所示。进行三阶张量的卷积时，当两个张量的通道数相同时（下图的图像和卷积核都为两通道），滑动操作和矩阵卷积一样，只需要在长和宽两个方向进行，卷积的结果是一个通道数为1的三阶张量。

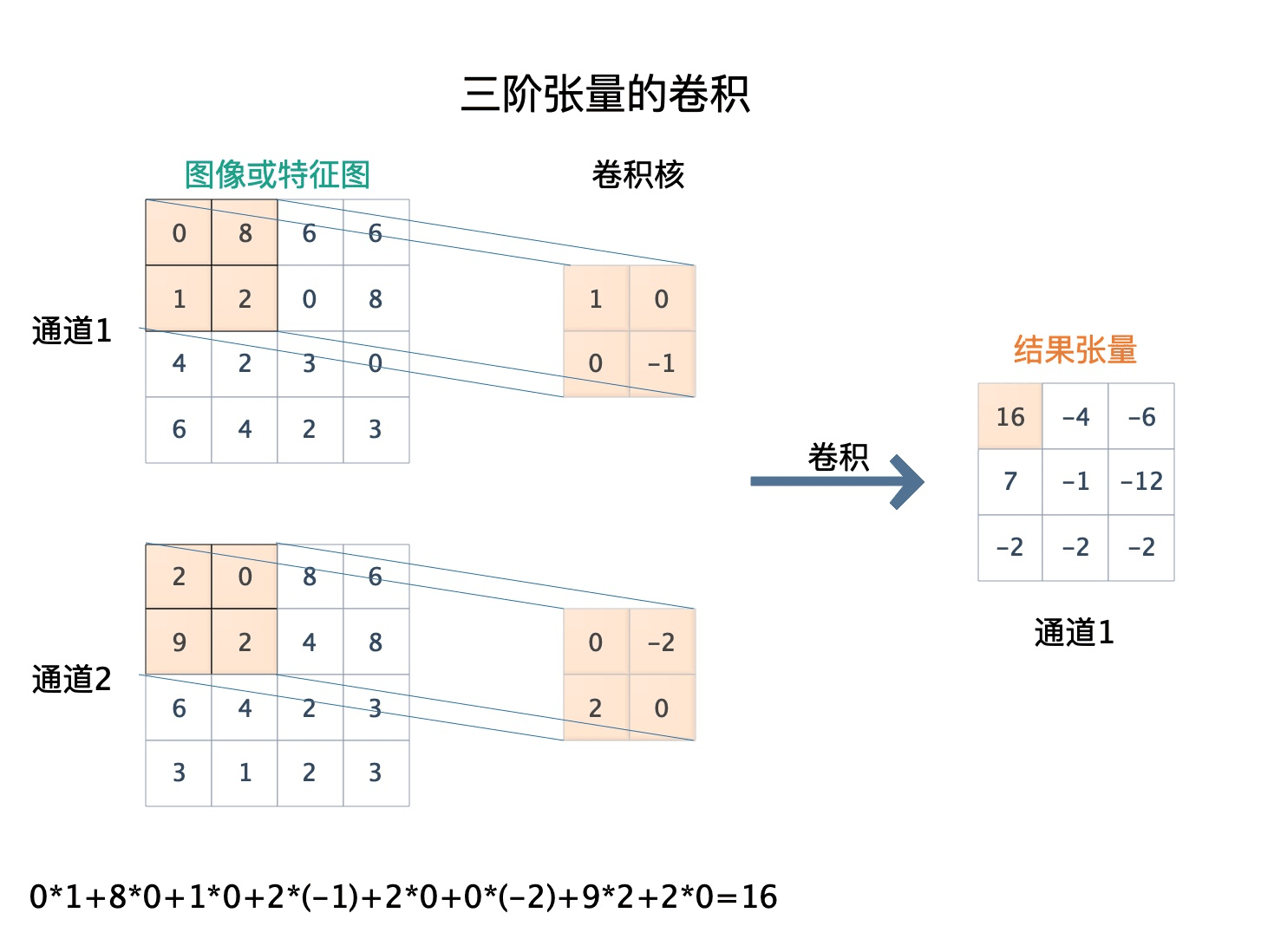
# 卷积计算
import tensorflow as tf


sess = tf.InteractiveSession()
input_x = tf.constant([
    [
        [[0., 2.], [8., 0.], [6., 8.], [6., 6.]],
        [[1., 9.], [2., 2.], [0., 4.], [8., 8.]],
        [[4., 6.], [2., 4.], [3., 2.], [0., 3.]],
        [[6., 3.], [4., 1.], [2., 2.], [3., 3.]],
    ]
], shape=[1, 4, 4, 2])

kernel = tf.constant([
    [
        [[1.], [0.]], [[0.], [-2.]],
        [[0.], [2.]], [[-1.], [0.]]
    ],
], shape=[2, 2, 2, 1])


conv2d = tf.nn.conv2d(input_x, kernel, strides=[
    1, 1, 1, 1], padding='VALID')

(sess.run(conv2d)).reshape(3, 3)

array([[ 16.,  -4.,  -6.],
       [  7.,  -1., -12.],
       [ -2.,  -2.,  -2.]], dtype=float32)

利用卷积提取图像特征

  卷积运算在图像处理中应用十分广泛，许多图像特征提取的方法都会用到卷积。以灰度图为例，灰度图在计算机的眼中被表示为一个整数的矩阵。如果我们使用一个形状较小的矩阵和这个图像矩阵做卷积运算，就可以得到一个新的矩阵，这个新的矩阵则可以看成是一副新的图像。通过卷积运算得到的新图像有时候比原图更清楚的表示了某些性质，我们就可以把他看成原图像的一个特征。而这里使用的小矩阵称为卷积核。

  通过卷积，我们可以从图像中提取边缘特征，所以在没有边缘的比较平坦的区域（物体内部），图像像素值的变化较小；由于0偏暗、255偏亮，而横向边缘两侧（物体侧边的两侧）的像素差异明显。如下图所示，我们利用了卷积核分别计算了原图像上每个3×3区域内左右像素或上下像素的差值（为了将运算结果以图像的形式展示出来，我们对运算结果取了绝对值）。

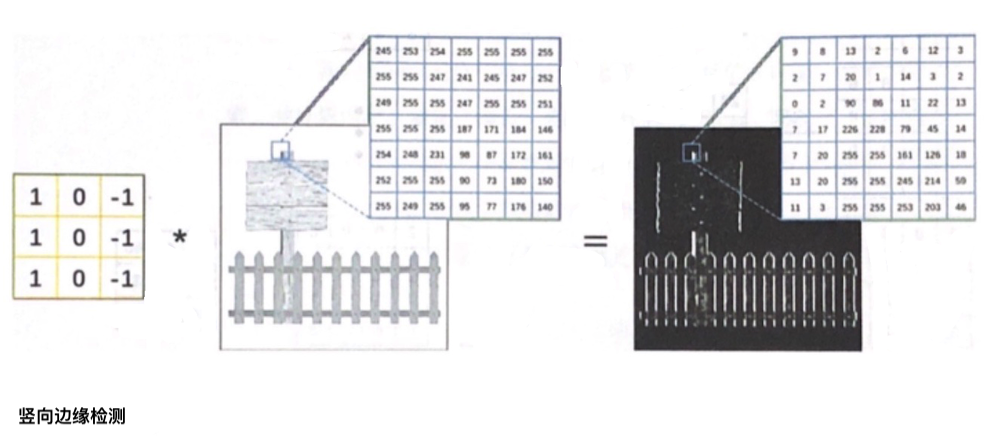
  上图我们使用了三列1、0、-1组成的卷积核与原图像进行卷积运算，可以从图像中提取出竖向边缘

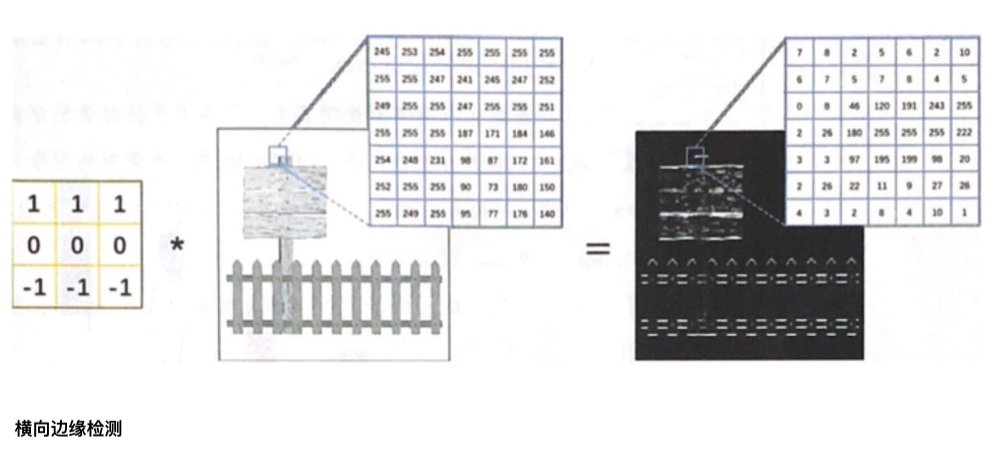
  上图我们使用了三行1、0、-1组成的卷积核，从图像中提取出了横向边缘。

基于神经网络的图像分类

传统图像分类系统和深度神经网络

  上一节，我们学会了如何手工设计图像特征，通过手工设计特征的过程可以发现手工设计图像特征是非常慢的，甚至有时候手工设计的图像特征毫无意义，因此导致图像分类的准确率曾经在一段时间内达到瓶颈。

# 2010-1017ImageNet挑战赛最低错误率图例
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

plt.style.use('ggplot')

years = ['2010', '2011', '2012', '2013',
         '2014', '人类', '2015', '2016', '2017']

years_index = range(len(years))
error_rates = [28.2, 25.8, 16.4, 11.7, 7.3, 5.2, 4.9, 3.5, 2.3]

plt.bar(years_index[:2], error_rates[:2],
        align='center', color='skyblue', label='传统方法')
plt.bar(years_index[2:5], error_rates[2:5],
        align='center', color='darkcyan', label='深度学习')
plt.bar(years_index[5:6], error_rates[5:6],
        align='center', color='gray', label='人类')
plt.bar(years_index[6:], error_rates[6:], align='center', color='darkcyan')

plt.xticks(years_index, years, rotation=0,
           fontsize=13, fontproperties=font)
plt.ylabel('分类错误率', fontproperties=font, fontsize=15)
plt.title('2010-1017ImageNet挑战赛最低错误率', fontproperties=font, fontsize=20)
plt.savefig(fname='2010-1017ImageNet挑战赛最低错误率图例')
plt.legend(prop=font)
plt.show()

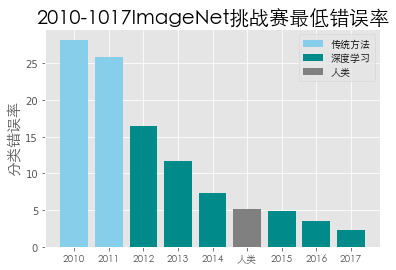
  在2012年之后，深度神经网络在Image Net挑战赛（图片识别挑战赛）中大放异彩，如上图所示，也因为深度神经网络的加入，在2015年的Image Net挑战赛中，微软团队研究的神经网络架构将图片识别的错误率降低到了4.9%，首次超过了人类的正确率，并且在2017年，图片分类错误率也达到了2.3%，这也是举办Image Net挑战赛的最后一年，因为深度神经网络已经很好地解决了图片分类的问题。

  深度神经网络之所以有这么强大的能力，就是因为他解决了传统图像分类中手工提取特征的缺点，而深度神经网络本身可以自动从图像中学习有效的特征。如下图所示看，之前传统的图像分类系统中，特征提取和分类是两个独立的步骤，而深度神经网络将两者集成在了一起。从这个角度来说，深度神经网络并不是在图像分类上做出某种创新，而是对传统的图像分类系统做出了改进与增强。

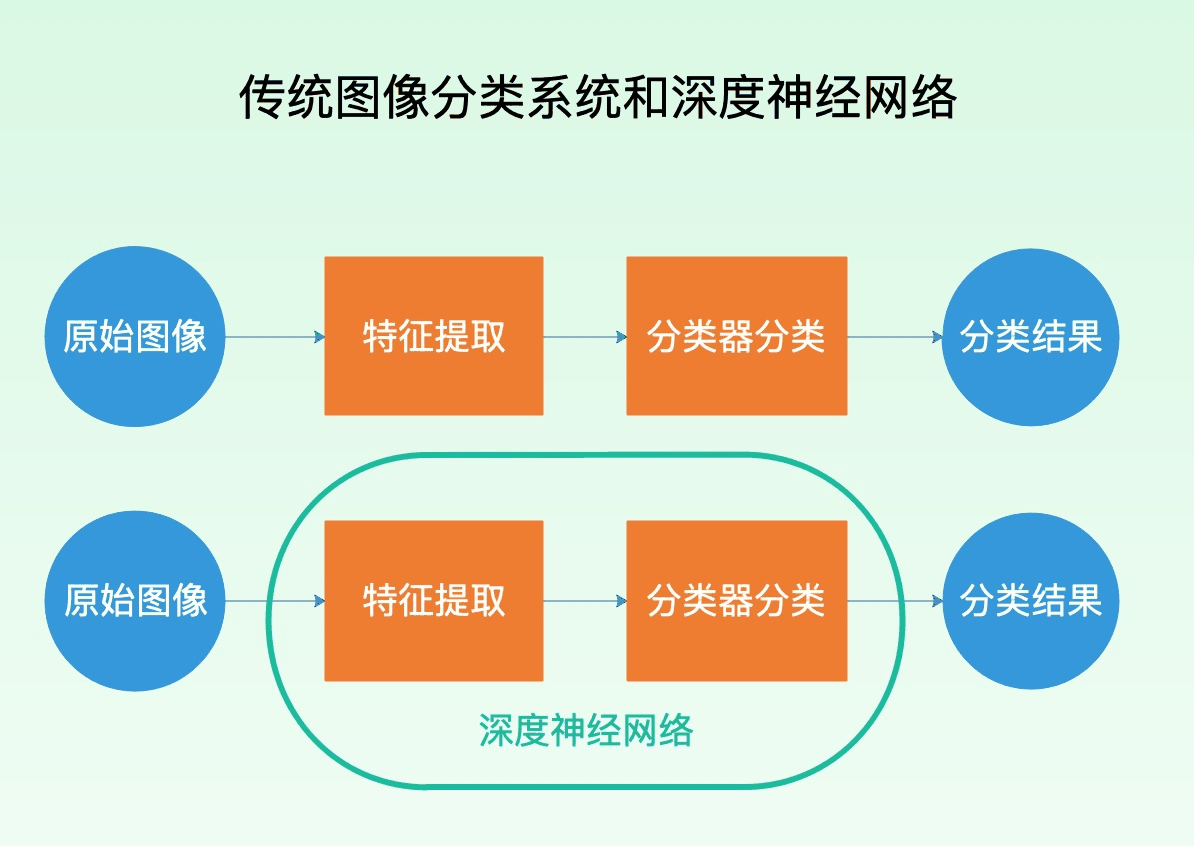
深度神经网络的架构

  一个深度神经网络通常由多个顺序连接的层构成。

1. 第一层一般是以图像为输入的输入层，通过某种特定的运算从图像中提取特征
2. 接下来每一层以前一层提取的特征为输入，通过特定形式的变换，得到一个更为复杂的特征
3. 重复上一步，对这种特征特定形式的变换进行累加，将原始图片转换为高层次的抽象的特征（因此赋予了神经网络强大的特征提取能力）

  上述深度神经网络的流程可以理解成我们日常学习英语的过程

1. 通过对字母的组合，得到单词
2. 通过单词的组合，得到句子
3. 通过句子的分析，了解句子的语义
4. 通过语义的分析，获得句子所表达的思想

其中句子的语义和句子所表达的思想，即为高级别的抽象的特征。

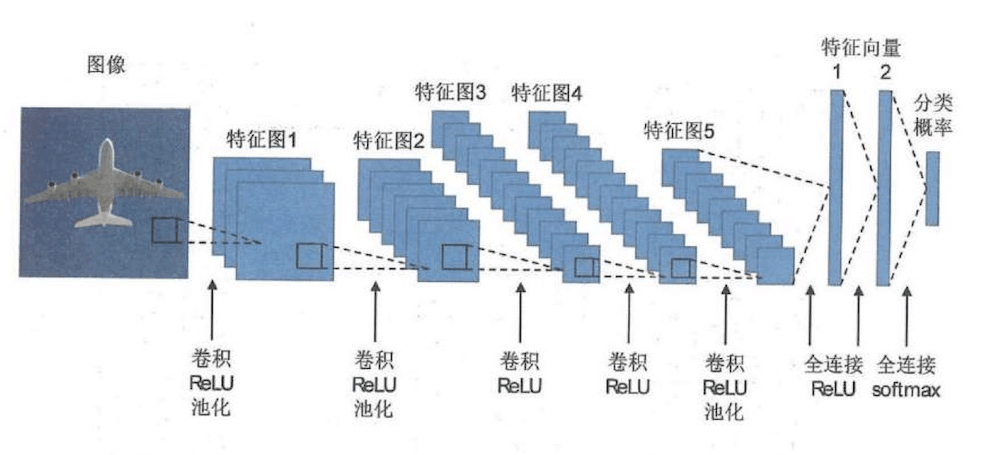
  上图所示的便是一个神经网络架构，该神将网络架构是由2012年获得Image Net挑战赛冠军的Alex Net神经网络架构。这个神经网络架构出现了卷积层、ReLU非线性激活层、池化层、全连接层、softmax归一化指数层等概念，之后会逐一介绍。

  这个神经网络由5个卷积层和3个全联接层组成。五个卷积层位于输入层右侧，依次对图像进行变化以提取特征。每个卷积层之后都会有一个ReLU非线性激活层完成非线性变换。上图5个卷积层中第一、二、五个卷积层之后连接有最大池化层，可以用来降低特征图分辨率。在上述流程中，经过5个卷积层和池化层之后，特征图转换为4096维的特征向量；再经过两次全连接层和ReLU层的变换之后，成为最终的特征向量；最后经过一个全连接层和一个softmax归一化指数层之后，即可得到对图片所属类别的预测。

卷积层

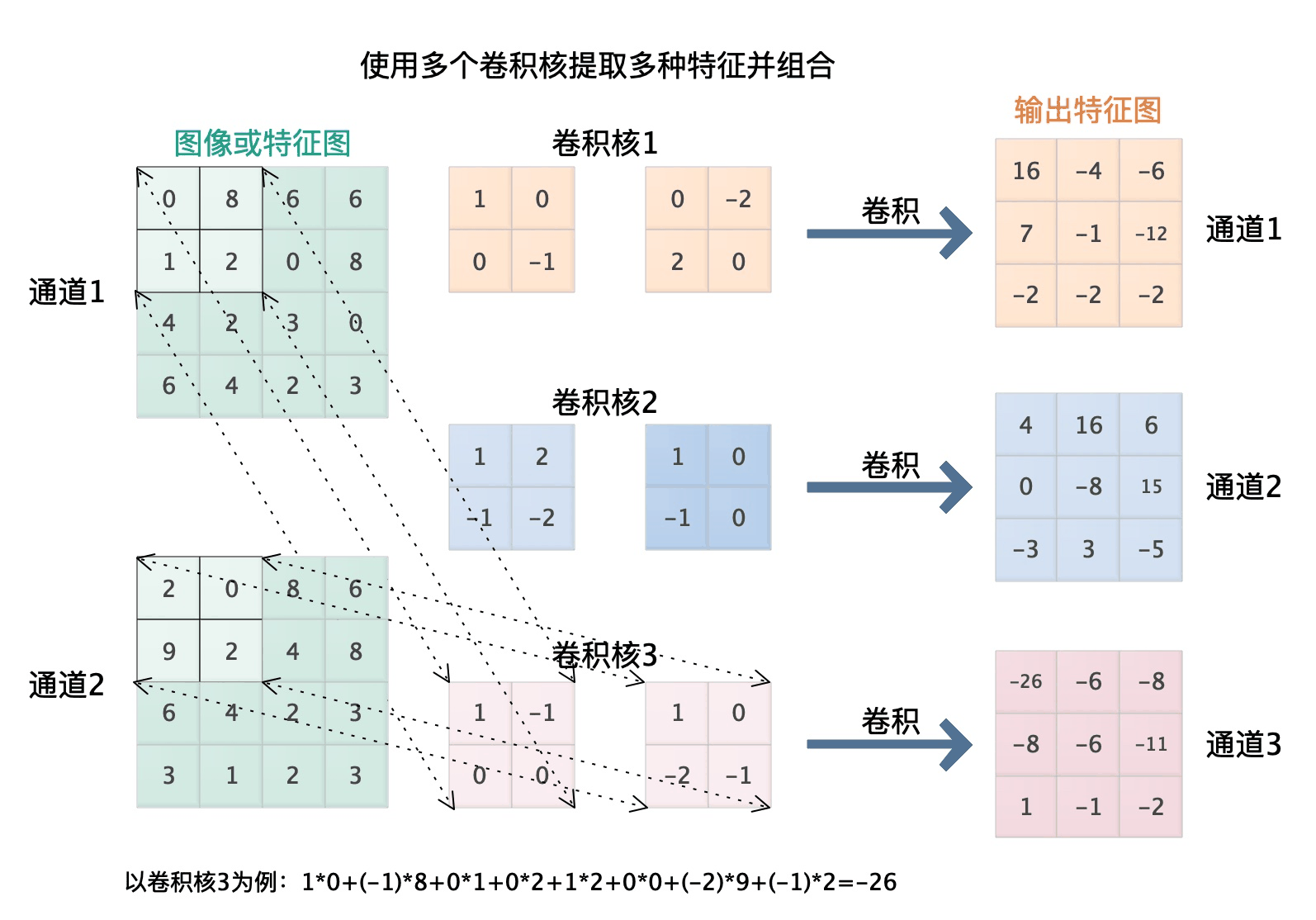
  卷积层是深度神经网络在处理图像时十分常用的一种层。当一个深度神经网络以卷积层为主体时，我们也会把这种深度神经网络称为卷积神经网络。卷积层主要的作用是使用卷积运算对原始图像或者上一层的特征进行变换的层，为了从图像中提取多种形式的特征，我们通常使用多个卷积核对输入图像进行不同的卷积操作，如下图所示。

# 卷积计算
import tensorflow as tf


sess = tf.InteractiveSession()
input_x = tf.constant([
    [
        [[0., 2.], [8., 0.], [6., 8.], [6., 6.]],
        [[1., 9.], [2., 2.], [0., 4.], [8., 8.]],
        [[4., 6.], [2., 4.], [3., 2.], [0., 3.]],
        [[6., 3.], [4., 1.], [2., 2.], [3., 3.]],
    ]
], shape=[1, 4, 4, 2])

kernel = tf.constant([
    [
        [[[1., 1., 1.], [0., 1., 1.]], [[0., 2., -1.], [-2., 0., 0.]]],
        [[[0., -1., 0.], [2., -1., -2.]], [[-1., -2., 0.], [0., 0., -1.]]]
    ],
], shape=[2, 2, 2, 3])


conv2d = tf.nn.conv2d(input_x, kernel, strides=[
    1, 1, 1, 1], padding='VALID')

(sess.run(conv2d))

array([[[[ 16.,   4., -26.],
         [ -4.,  16.,  -6.],
         [ -6.,   6.,  -8.]],

        [[  7.,   0.,  -8.],
         [ -1.,  -8.,  -6.],
         [-12.,  15., -11.]],

        [[ -2.,  -3.,   1.],
         [ -2.,   3.,  -1.],
         [ -2.,  -5.,  -2.]]]], dtype=float32)

  从上图可以看出一个卷积核可以得到一个通道为1的三阶张量，多个卷积核就可以得到多个通道为1的三阶张量结果。我们把这些结果作为不同的通道组合起来，即可以得到一个新的三阶张量，这个三阶张量的通道数为我们使用的卷积核的个数。由于每一个通道都是从原图像中提取的一种特征，我们有时候也会把这个三阶张量称为特征图，这个特征图就是卷积层的输出。

  也就是说如果一个神经网络有多个卷积层，第一个卷积层以图像作为输入，而之后的卷积层会以前面的层输出的特征图作为输入。

池化层

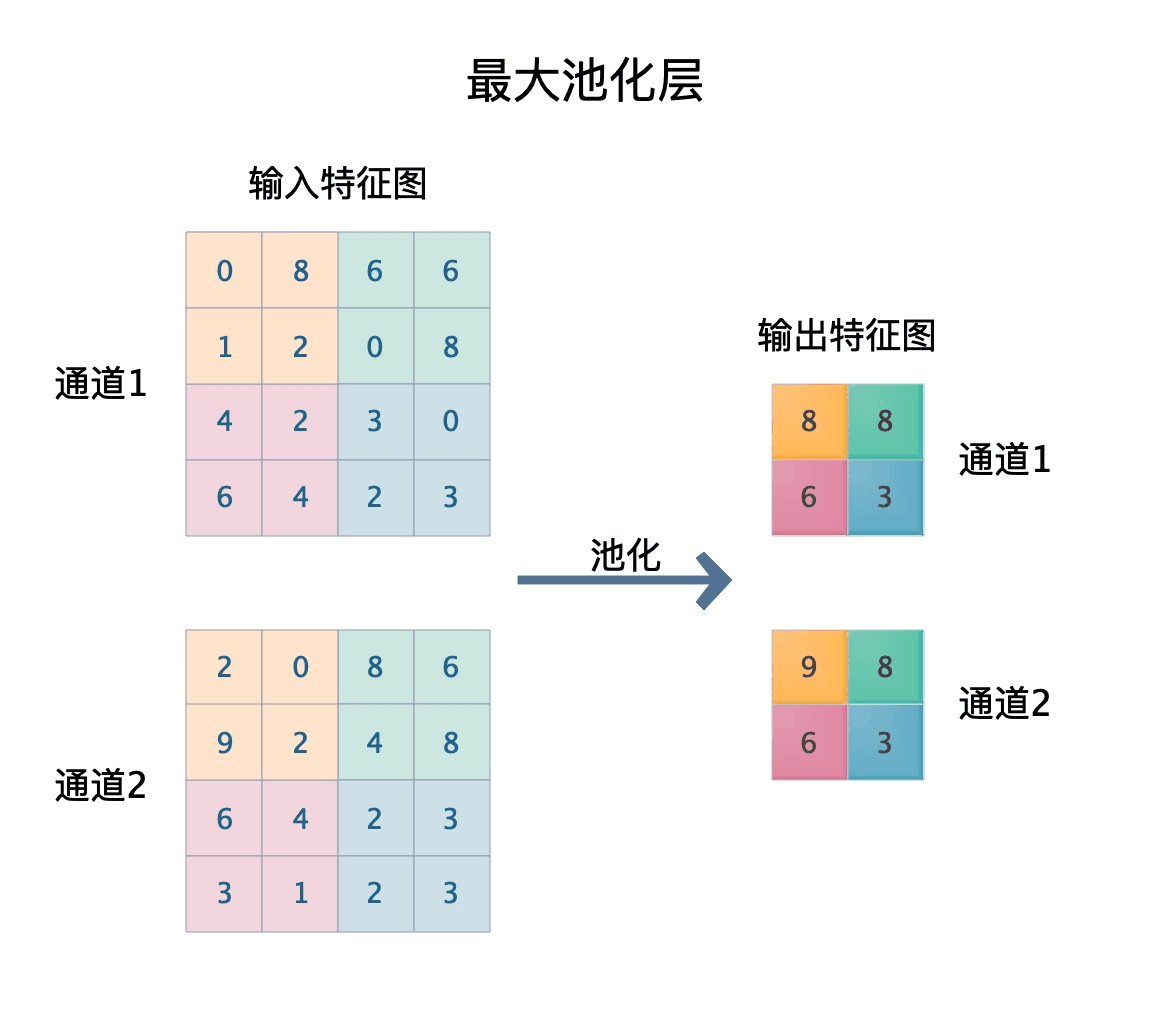
  在讲解卷积层的时候，我们假设图像的分辨率是4*4，但是如果图像或者特征图的分辨率很大，由于卷积核会滑过图像或特征图的每一个像素，那么卷积层的计算开销会很大。为了解决这个问题，我们一般会使用池化层降低特征图的分辨率。最大池化层的步骤如下图所示。

  如上图所示：

1. 首先我们将特征图按通道分开，然后对于每个通道对应的矩阵，将其切割成若干个大小相等的正方形小块。上图我们将4×4的矩阵切割成4个2×2的正方形小块。
2. 切割矩阵之后，对每个正方形小块取最大值和平均值，并将结果组成一个新的矩阵。
3. 将所有通道的结果矩阵按原顺序堆叠形成一个三阶张量，这个三阶张量就是池化层的输出。

  对每一个区块取最大值的池化层，我们称之为最大池化层；对于取平均值的池化层，我们称之为平均池化层。上图经过池化层处理，特征图的长和宽都会减小到原来的一半，即特征图的分辨率减小了一半，大大减小了计算开销。

全连接层

  当图像经过多层卷积层处理之后，会将得到的特征图转换为特征向量。全连接层的作用则是对这个特征向量做处理。

  在全连接层中，我们会使用若干维数相同的向量与输入向量（特征向量）做内积操作，并且将所有结果拼成一个向量作为输出。即假设全连接层以一个向量\(X=(x_1,x_2,\cdots,x_n)\)作为输入，我们会用\(K\)个维数相同的参数(K一般等于类别个数)向量\(W_k=(w_{k1},w_{k2},\cdots,w_{kn})\)与\(X\)做内积运算，并且在每个结果上面加上标量\(b_k\)（偏置单元），即完成
\(y_k=X·W_k+b_k，k=1,2,3,\cdots,K\)的运算。最后我们将\(K\)个标量结果\(y_k\)组成向量\(Y=(y_1,y_2,\cdots,y_K)\)作为这一层的输出。

归一化指数层

  归一化指数层（softmax layer）一般是分类网络的最后一层，它以一个长度和类别个数相等的特征向量作为输入（一般这个特征向量是全连接层的输出），然后输出图像属于各个类别的概率。

非线性激活层

  再讲非线性激活层之前，我们首先要回过头去看我们之前的卷积层和全连接层，我们可以发现卷积层和全连接层中的运算都是关于自变量的一次函数，即所谓的线性函数。而线性函数有一个性质，若干个线性函数复合时，只是自变量在不断的变化，复合后的函数仍然是线性的。也就是说，如果不使用非线性激活层，我们只是将卷积层和全连接层直接堆叠起来，那么他们对输入图片产生的效果就可以被一个全连接层替代。如此做的话，我们虽然堆叠了很多层，但每一层的变换效果实际上被合并到了一起。

  如果在每次线性计算后，我们再进行一次非线性运算，那么每次变换的效果将可以保留。神经网络中的非线性激活层方式有很多种，但是他们的基本形式都是对特征图或特征向量中的每一个元素，使用某种你非线性函数进行转换，然后得到输出。

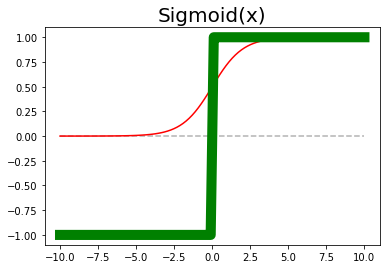
Sigmoid函数

  Sigmoid函数是较为原始的激活层使用的方法，可以在卷积层将数据扩大之后，把数据压缩在0-1之间。

\[s(x)=\frac{1}{1+e^{-x}} \]

# Sigmoid激活函数图例
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10, 10, 100)
y = (1/(1+np.e**(-x)))
y2 = np.sign(x)

plt.hlines(0, -10, 10, alpha=0.3, linestyles='--')
plt.plot(x, y, c='r')

plt.title('Sigmoid(x)', fontsize=20)
plt.show()

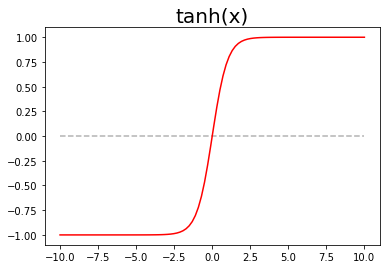
双曲正切函数

  双曲正切函数相比较激活函数可以减轻梯度消失的影响。

\[tanh(x)=\frac{e^x-e^{-x}}{e^{-x}+e^{-x}} \]

# 双曲正切激活函数图例
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10, 10, 100)
y = np.tanh(x)

plt.hlines(0, -10, 10, alpha=0.3, linestyles='--')
plt.plot(x, y, c='r')

plt.title('tanh(x)', fontsize=20)
plt.show()

ReLU函数

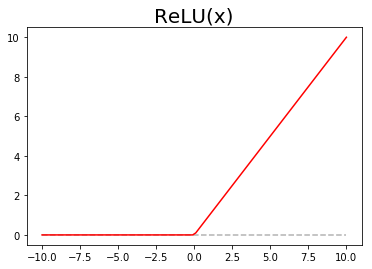
  ReLU激活函数如下图所示，ReLu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。并且ReLU激活函数将小于零的元素变成零，而保持其余元素的值不变。因此ReLU的计算非常简单，所以他的计算速度往往比其他非线性激活层快很多，并且他在实际应用中的效果非常好，因此在深度神经网络中被广泛的使用。

\[ReLU(x)= \begin{cases} 0, & x<0 \\ x, & x\geq{0} \end{cases} \]

# ReLU激活函数图例
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10, 10, 100)
y = np.where(x < 0, 0, x)

plt.hlines(0, -10, 10, alpha=0.3, linestyles='--')
plt.plot(x, y, c='r')

plt.title('ReLU(x)', fontsize=20)
plt.show()

深度神经网络的训练

  传统的分类器需要经过训练才可以区分属于不同类别的特征向量，深度神经网络也需要通过训练才能学习出有效的图像特征，两者相同之处都是在训练的过程中找打最佳参数的组合。在线性分类器中，参数包括线性函数的所有系数；在神经网络中，卷积层中所有的卷积核的元素值、全连接层所有内积运算的系数都是参数。为了将4个特征的鸢尾花数据分类，我们只需要训练5个参数；而在Alex Net中，需要学习的参数多达六千万个，其难度远高于线性分类器的训练。因此为了解决神经网络参数多，难训练的问题，科学家们提出了反向传播算法，如下图所示。

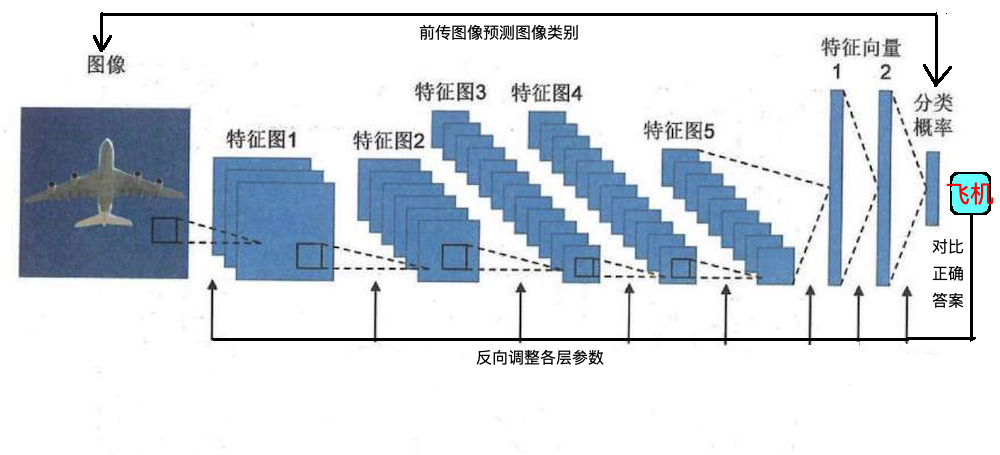
反向传播算法

  反向传播算法的流程为：

1. 将训练图片输入网络中，经过逐层的计算，得到最终预测的结果
2. 将预测结果和正确答案进行对比，如果预测结果不够好，那么会从最后一层开始，逐层调整神经网络的参数，使得网络对这个训练样本能够做出更好的预测
3. 具体的调整算法有随机梯度下降（此处不多赘述）

图像分类应用——人脸识别

  随着科技的发展，图像分类技术在日常生活中已经处处可见，有着广泛的应用，如人脸识别、图像搜索等。2014年，香港中文大学团队的工作使得机器在人脸识别任务上的表现第一次超越了人类，从此“人脸识别”也成为了深度学习算法着力研究的任务之一，并在不断的发展和演进中变成了最先实现落地和改变我们生活的深度学习应用之一。接下来我们主要介绍图像你分类计数在人脸识别上的应用。

人脸识别的流程

  人脸识别是从一张数字图像或一帧视频中，由“找到人脸”到“认出人脸”的过程，其中“认出人脸”就是一个图像分类的任务。人脸识别的整个流程可以包括以下几个步骤：人脸检测、特征提取、人脸对比和数据保存。

• 人脸检测：人脸检测就是对含有用户脸部的图像检测，找到人脸所在的位置、人脸角度等信息，人脸检测就是我们本章最早提出的人脸定位的问题。也就是完成“看到”的过程。
• 特征提取：特征提取可以通过对人脸检测到的人脸进行分析，得到人脸相应的特征，如五官等特点。也就是完成“看得懂”的过程
• 人脸对比：人脸对比则是拿特征提取提取的特征与数据库中已经记录的人像（如身份证照片）以一定的方法相比对。也就是完成“和谁像”的过程。
• 数据保存：这些分析结果最终将会保存， 服务于最终的实际应用场景。

人脸识别应用场景

话不多说，上图！

• 无人便利店

• 银行取钱

• 刷脸消费

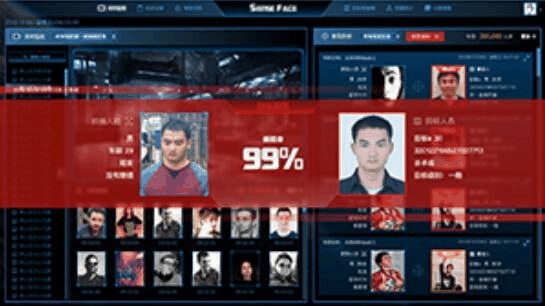
• 人脸布控系统

小结

  通过本章的对神经网络的描述，我们学习了以下几个知识点：

1. 我们了解了看起来高大上的卷积运算，并了解了如何使用卷积运算提取图像特征。
2. 由于手工设计特征的局限性较大，所以本章重点介绍了如何使用深度神经网络进行图像分类。
3. 在神经网络中，我们主要介绍的是卷积神经网络架构，并且介绍了卷积神经网络架构中的卷积层、池化层、全连接层、非线性激活层和会议华指数层。
4. 由于神经网络相比较传统的分类器，有较多的参数，为了解决训练难的问题，我们可以利用反向传播算法进行网络训练。
5. 最后，我们介绍了神将网络的图像分类目前在日常生活中的应用。